Übungen zur Vorlesung Klassische Mechanik WS 2003/04 Prof. Dr

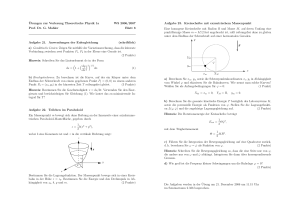
Übungen zur Vorlesung Klassische Mechanik
Prof. Dr. G. Mahler
WS 2003/04
b) Lösen Sie die Bewegungsgleichung für v mit der Anfangsbedingung
Blatt 10
t0 = 0 : v0 = 0.
Was ist die vom System gegen Reibung abgegebene Leistung?
(2 Punkte)
Aufgabe 39. Kontrollfragen
Aufgabe 42. Teilchen im Kreiszylinder
a) Was ist eine zyklische Koordinate?
b) Unter welchen Umständen ist der „(kanonisch) konjugierte“ Impuls verschieden
vom „kinematischen“ Impuls?
c) Was besagt das Noether-Theorem?
d) Mit welchen Symmetrien sind Energieerhaltung, Impulserhaltung bzw. Drehimpulserhaltung verknüpft?
Aufgabe 40. Lagrange 2. Art mit Reibung
z
Ein Massenpunkt m bewegt sich im homogenen
Schwerefeld auf der Innenseite eines Kreiszylinders (Radius R), dessen Achse mit der Vertikalen den Winkel α einschließt. PSfrag replacements
g
α
Bestimmen Sie die Lagrangefunktion und die
Bewegungsgleichungen.
(2 Punkte)
y
(schriftlich)
x
Für ein mechanisches System mit skleronom-holonomen Zwangsbedingungen sei
Aufgabe 43. Teilchen im Paraboloid
L = L(qβ , q̇β ) = T − V (qβ )
Ein Massenpunkt m bewegt sich ohne Reibung an der Innenseite einer axialsymmetrischen Paraboloid-Mantelfläche, gegeben durch
und die Dissipationsfunktion
εD =
f
1 X
cαβ q̇α q̇β .
2 α,β=1
z=
1
b (x2 + y 2 ),
2
wobei b eine Konstante ist und z in die vertikale Richtung zeigt:
Welche allgemeine Form hat T ?
Zeigen Sie, dass
z
d
(T + V ) = −2 εD .
dt
(4 Punkte)
PSfrag replacements
g
z0
Aufgabe 41. Freier Fall mit Reibung
Ein Teilchen der Masse m falle vertikal unter dem Einfluss der Schwerkraft, wobei
Reibung gemäß der Dissipationsfunktion
εD =
1 2
αv
2
auftreten möge (α = const, v = Betrag der Geschwindigkeit).
a) Was sind hier die angepassten Koordinaten? Bestimmen Sie die Lagrangefunktion
sowie die Lagrangegleichung mit Reibung.
(2 Punkte)
θ r
y
x
a) Bestimmen Sie die Lagrangefunktion. Der Massenpunkt bewege sich in einer
Kreisbahn in der Höhe z = z0 . Bestimmen Sie die Energie und den Drehimpuls in
Abhängigkeit von z0 , b, g und m.
(3 Punkte)
b) Der Massenpunkt in der horizontalen Kreisbahn wird (wenig) nach unten gestoßen. Bestimmen sie die Schwingungsfrequenz um die ungestörte Kreisbahn bei einer
kleine Schwingungsamplitude.
(2 Punkte)