Übungen zur Theoretischen Festkörperphysik: Vertiefung (TV

Übungen zur Theoretischen Festkörperphysik: Vertiefung (TV-2)
Lösung:
9. Präsenzübung am 3. Juli 2014
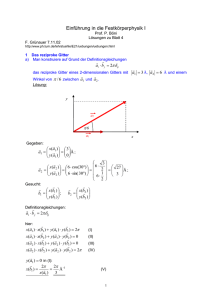
P18 Kristallstruktur von Graphen: ein zweidimensionales KohlenstoffGitter
C
Betrachten
Sie
das
skizzierte
Kristallgitter von Graphen. Es handelt sich um ein Honigwabengitter
mit dem Bindungsabstand
a
≈
1, 42 Å zwischen zwei
Kohlenstoff-Atomen.
a) Die y-Komponenten der beiden Vektoren erhält man aus der halben Höhe h einer
“Honigwabe” mit der Kantenlänge a:
h
1√ 2
1
2π 1/2
a√
=
=
2a2 − 2a2 cos
3a =
3.
2
2
3
2
2
Um die x-Komponenten zu bestimmen, betrachten wir folgende Skizze:
C
s=
a/2
y
x
a1
a
a1
a
a2
h
a) Bestimmen Sie die beiden skizzierten Translationsvektoren a1 und a2 im (x, y)-Koordinatensystem.
b) Skizzieren Sie die Elementarzelle. Wie viele Atome enthält diese? Welches Gitter wird
durch die Translationsvektoren a1 und a2 - von einem Punkt startend - erzeugt?
c) Bestimmen Sie die beiden reziproken Gittervektoren b1 und b2 mit Hilfe der Bedingungen
b1 · a1 = b2 · a2 = 2π und b1 · a2 = b2 · a1 = 0 .
d) Skizzieren Sie das reziproke Gitter und konstruieren Sie die Brillouinzone.
y
Die Länge der Strecke s ist a2 . Damit erhält man, dass die x-Komponente von a1 und
a2 gleich a + a2 = 23 a ist. Zusammengefasst erhält man also die beiden Vektoren
√ a
a √ und a2 =
a1 =
3, 3
3, − 3 .
2
2
b) Die Elementarzelle enthält 2 Atome:
b1
In den Ecken der Brillouinzone von Graphen
befinden sich die beiden Punkte K und K′ (siehe
e)
Skizze). Bestimmen Sie die Vektoren K und K′ .
Drücken Sie sie auch durch b1 und b2 aus.
a2
K
a
a1
Γ
x
K’
a2
b2
f) Die Translation einer Wellenfunktion am Punkt k in der Brillouinzone um den Vektor
Rn = a1 n1 + a2 n2 erzeugt nach dem Bloch-Theorem einen Phasenfaktor eikRn , d.h.
Ψk (r + Rn ) = eikRn Ψk (r).
i) Bestimmen Sie das Translationsverhalten einer Wellenfunktion ΨΓ (r) am ΓPunkt.
ii) Wie transformiert sich eine Wellenfunktion am K-Punkt bei der Translation
um Rn ? Welche Phase erhält die Wellenfunktion bei der Translation in die
Nachbarzellen des Graphen-Gitters?
iii) Bestimmen Sie ebenso die Transformation der Wellenfunktion am K′ -Punkt bei
einer Translation um den Vektor Rn .
Begründen Sie damit, warum man
∗
ψK = ψK
′
wählen kann, d.h. die Wellenfunktion am K-Punkt ist die komplex Konjugierte der
Wellenfunktion am K′ -Punkt.
Würde man von einem Punkt aus starten, so würden die Translationsvektoren a1 und
a2 ein Dreiecksgitter erzeugen.
c) Aus den Bedingungen b1 · a1 = 2π und b1 · a2 = 0 erhält man die beiden Gleichungen
√
3a y
3a x
b1 +
b = 2π
2
2 1
und
√
3a x
3a y
b1 −
b =0
2
2 1
mit der Lösung
2π √ b1 =
1, 3 .
3a
Analog findet man:
√ 2π b2 =
1, − 3 .
3a
d) Reziprokes Gitter und Brillouinzone:
iii) Ebenso kann man bestimmen, dass die Wellenfunktion am K ′ -Punkt bei einer
Translation um den Vektor Rn die Phase
b1
e2πi
erhält. Wegen
K
Γ
b1 + b2
K
K · Rn + K′ · Rn = 2π
′
e) Aus den Vektoren b1 und b2 erhält man die Vektoren K und K′ :
1
1
1
2π
K = [b1 + (b1 + b2 )] = (2b1 + b2 ) =
1, √
3
3
3a
3
K′ =
f)
1
2π
1
[b2 + (b1 + b2 )] = (2b2 + b1 ) =
3
3
3a
1
1, − √
3
i) Am Γ-Punkt ist k = 0, damit gilt für die Transformation einer Wellenfunktion
am Γ-Punkt ϕΓ :
T̂n ϕΓ = ϕΓ ,
da eik·Rn = 1 für k = 0.
ii) Am K-Punkt erhält eine Wellenfunktion die Phase
2
1
eiK·Rn = ei( 3 b1 + 3 b2 )·(a1 n1 +a2 n2 )
2
1
= ei( 3 n1 (b1 ·a1 )+ 3 n2 (b2 ·a2 ))
=
2n1 +n2
3
e2πi
.
Bei einer Translation in die Nachbarzellen erhält die Wellenfunktion also abwechselnd die Phase − 2π
und 2π
(die Werte in Klammern geben die Phase an, die
3
3
eine Wellenfunktion am K′ -Punkt bei den entsprechenden Translationen erhält):
2π
3
( 23π )
(
2π
3
)
2π
3
2π
3
2π
3
)
( 23π )
a1
a2
(
2π
3
2π
3
3n1 + 3n2
= 2π (n1 + n2 )
3
ist klar, dass die Phase, die eine Wellenfunktion am K-Punkt bei einer beliebigen
Translation erhält, die komplex konjugierte der Phase ist, die eine Wellenfunktion
am K′ -Punkt bei der selben Translation erhält, ist. Das motiviert, dass
b2
und
2n2 +n1
3
( 23π )
2π
3
(
2π
3
)
∗
ψK = ψK
′ .
Übungen zur Theoretischen Festkörperphysik: Vertiefung (TV-2)
Lösung:
11. Hausaufgabe, Abgabe: 8. Juli 2014, 10 c. t. (Kasten im Hörsaal)
H23 Einfach kubisches Gitter und NaCl-Gitter
a) Das NaCl-Gitter ist ebenfalls ein FCC Gitter, allerdings mit einer zweiatomigen Basis.
Die Translationsvektoren sind in der folgenden Abbldung zu sehen
In dieser Aufgabe sollen Sie sich mit den elementaren Begriffen der Theorie der Kristalle vertraut machen. Dazu betrachten Sie das NaCl-Gitter (auch als Kochsalz bekannt) bestehend
aus zwei ineinander geschachtelten kubisch-flächenzentrierten (FCC) Gittern von Natrium
und Chlor, deren Gitterkonstante gleich ist. Dabei liegt das Basisatom des einen Gitters in
der Raummitte des Kubus des anderen Gitters.
Es ist in folgender Abbildung zu sehen.
a3
a2
a1
a
a) Welchen Gittertyp (z.B. Flächenzentriert (FCC), Volumenzentriert (BCC), einfach
kubisch (SC) usw.) besitzt das NaCl-Gitter und aus wie vielen Atomen besteht seine
Basis? Tragen Sie in die Zeichnung insbesondere die elementaren Translationsvektoren
a1 , a2 , a3 ein.
b) Es entstünde ein einfach kubisches Gitter (SC). Ausgedrückt durch die Basisvektoren
c1 , c2 und c3 des einfach kubischen Gitters lauten die Basisvektoren des FCC Gitters:
a1
=
c1 + c2
a2
=
c2 + c3
a3
=
c3 + c1 .
Die Basisvektoren sind dann in der folgenden Abbildung zu sehen:
b) Welchem elementaren Gittertyp entspräche das Gitter, wenn dieses nur aus gleichartigen Atomen bestünde, d.h. wenn also auf allen Gitterplätzen nur Na-Atome oder nur
Cl-Atome säßen? Zeichnen Sie auch dieses Gitter inklusive der neuen Basisvektoren
c1 , c2 , c3 . Bestimmen Sie anschließend den Zusammenhang zwischen {ai } und {cj }.
c) Berechnen Sie die Volumina der Elementarzellen beider Gitter als Funktion der Gitterkonstante a.
c3
c1
d) Berechnen Sie die reziproken Gittervektoren b1 , b2 und b3 bzw. d1 , d2 und d3 beider
Gitter.
c2
e) Skizzieren Sie die beiden reziproken Gitter. Um welche Gittertypen handelt es sich
bei den reziproken Gittern?
f) Konstruieren Sie die Brillouinzonen beider Gitter. Verschieben Sie den Ursprung des
reziproken einfach kubischen Gitters so, dass die zum FCC Gitter gehörende Brillouinzone innerhalb der einfach kubischen Brillouinzone liegt.
g) Aus dem NaCl erhält man eine Zinkblendestruktur, wenn man die die beiden FCC
Untergitter des NaCl Gitters derart gegeneinander verschiebt, dass sich ein Na-Atom
in perfekt tetraedrischer Umgebung eines Cl-Atoms befindet. Zeichnen Sie die Verschiebung und das Gitter. Welche Gitterstruktur entstände in diesem Fall, wenn alle
Atome identisch wären?
c) Das Elementarzellenvolumen des SC Gitters ist trivialerweise das Würfelvolumen:
ΩSC = a3
Das Elementarzellenvolumen des FCC Gitters findet man durch Berechnung des Spatproduktes:
ΩF CC = a1 · (a2 × a3 ) = (c1 + c2 ) · [(c2 + c3 ) × (c3 + c1 )]
= (c1 + c2 ) · (c1 − c3 + c2 ) c = 2a3 .
d3
d) Die reziproken Gittervektoren des einfach kubischen Gitters lauten:
d1
=
d2
=
d3
=
2π
2π
c2 × c3 = 2 c1
c3
c
2π
c2
c2
2π
c3 .
c2
Γ
d1
Die reziproken Gittervektoren des FCC Gitters findet man analog:
b1
=
b2
=
b3
=
2π
2π
a2 × a3 = 2 (c1 + c2 − c3 )
ΩF CC
2c
2π
(c2 + c3 − c1 )
2c2
2π
(c1 + c3 − c2 ) .
2c2
g) Durch eine Verschiebung des Gitters FCC2 um den Vektor u erhält man eine ZinkBlende Struktur:
1
u
1
2
e) Beim reziproken Gitter des FCC Gitters handelt es sich um ein BCC Gitter. Das
reziproke Gitter des einfach kubischen Gitters ist wieder ein einfach kubisches Gitter.
1
d3
d2
1
b2
Sind alle Atome gleich, so ergibt sich ein Diamant-Gitter.
b3
d2
d1
b1
f) Brillouinzone des FCC Gitters:
d3
b2
b3
d2
d1
Brillouinzone des einfach kubischen Gitters:
b1