2.20 Impuls Wirkung einer Kraft auf einen K癢rper durch Angabe der

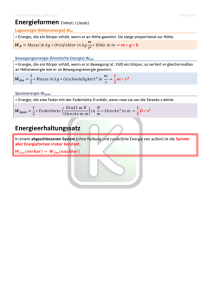
2.20 Impuls
~ noch nicht eindeutig bestimmt: hÄ
Wirkung einer Kraft auf einen KÄorper durch Angabe der F
angt
noch von der KÄorpereigenschaft m ab:
~
v
F
~a = d~
dt = m Umschreiben dieser Gleichung (etwa entsprechend einer Trennung: was kommt von
au¼en? was betri®t KÄorper?):
~ dt = md~v = d(m~v )
F
|{z}
|{z}
v:aussen
(fÄ
ur m = const)
neue GrÄ
o¼e eingefÄ
uhrt: ~p := m~v
Koerper
Impuls
R
~ (t)dt = 4~
~ dt bewirkt ImpulsÄ
) F
p
Kraftsto¼ F
anderung d~
p
~
~
~
z.B. fÄ
ur F (t) = const:
F 4t = 4~p ) ~p(t + 4t) = p~(t) + F 4t
Anmerkungen:
1.) Die relativistisch korrekte De¯nition fÄ
ur den Impuls lautet ~
p = m~v ¢ ° mit dem sogenannten
v 2 ¡ 12
"Lorentzfaktor" ° = (1 ¡ c2 ) . Mit v ! c steigt ° viel stÄ
arker an als v. d.h. eine Kraft wird dann
vorwiegend dafÄ
ur verwendet, um ° zu vergrÄ
o¼ern.
2.) Widerstand gegen eine Beschleunigung ~a ("TrÄ
age Masse") und Ansprechen auf ein Gravitationsfeld ("schwere Masse") sind also von der Geschwindigkeit v eines KÄ
orpers und damit von ° abhÄ
angig.
Der KÄ
orper verhÄalt sich so, als hÄatte er in der Newtonschen Mechanik die Masse mR = m°, die man
deshalb etwas unschÄon als die 'relativistische Masse' des KÄ
orpers bezeichnet. Die den KÄ
orper charakterisierende GrÄo¼e ist natÄ
urlich seine Ruhemasse m.
Zwei nÄ
utzliche Beziehungen fÄ
ur ein System von Teilchen:
pgesamt =
~
P
i
~pi =
P
d
r
i dt mi ~
=
d
dt
P
i
mi ~ri =
d
rsp
dt Mk ~
= Mk~vsp = p~sp
d.h. Der Impuls eines KÄ
orpers = Impuls seines Massenmittelpunktes (Schwerpunkts SP).
~ges = P F
~i = P d ~pi =
F
dt
d
dt
P
p~i =
d
d
p~ (= dt
pges )
~
dt sp
Ä
Die Anderung
der Summe der Einzelimpulse = der gesamten auf das System wirkenden Kraft.
~ges = 0
insbesondere gilt fÄ
ur F
d
dt
P
pi = 0 )
~
P
pi = const
~
Diese Formel stellt den wichtigen Satz von der Erhaltung des Gesamtimpulses in einem abgeschlossenen System dar.
1