a) b) 2. - turniersystem.de

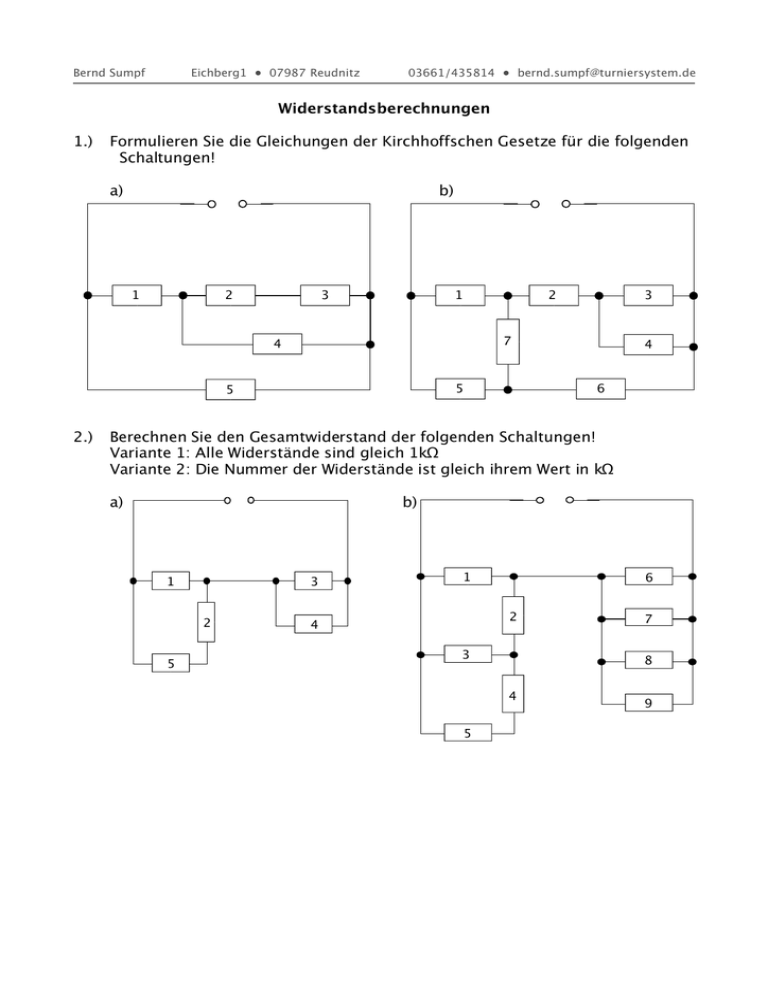
Bernd Sumpf
Eichberg1 • 07987 Reudnitz
03661/435814 • [email protected]
Widerstandsberechnungen
1.)
Formulieren Sie die Gleichungen der Kirchhoffschen Gesetze für die folgenden
Schaltungen!
a)
b)
1
2
3
1
2
7
4
5
5
2.)
3
4
6
Berechnen Sie den Gesamtwiderstand der folgenden Schaltungen!
Variante 1: Alle Widerstände sind gleich 1kΩ
Variante 2: Die Nummer der Widerstände ist gleich ihrem Wert in kΩ
a)
b)
1
3
2
5
1
6
2
4
3
8
4
5
7
9
Bernd Sumpf
3.)
a)
Eichberg1 • 07987 Reudnitz
03661/435814 • [email protected]
Zeichnen Sie den Ersatzschaltplan!
1
12
11
2
3
4
10
9
6
7
8
5
b)
4.)
Berechnen Sie den Gesamtwiderstand, wenn alle Widerstände 100 Ohm
betragen!
Versuchen Sie, mit möglichst wenigen 1kΩ-Widerständen einen
Gesamtwiderstand von 150 Ω darzustellen!
Bernd Sumpf
Eichberg1 • 07987 Reudnitz
03661/435814 • [email protected]
Lösungen:
1.)
2.)
a)
U1 + U2 + U3 - Uges = 0
U1 + U4 - U5 = 0
U2 + U3 - U4 = 0
Iges – I1 – I5 = 0
I1 – I2 – I4 = 0
I2 – I3 = 0
b)
U1
U1
U3
U2
Iges – I1 – I5 = 0
I5 + I7 – I6 = 0
I1 – I2 – I7 = 0
I2 – I3 – I4 = 0
a)
linker Teil:
+ U2 + U3 - Uges = 0
+ U7 - U5 = 0
- U4 = 0
+ U4 - U6 - U7 = 0
R2 + R5 parallel zu R1
 R 2  R 5 ⋅ R1
R links =
= 0,667 kΩ
 R 2  R 5   R1
= 0,875 kΩ
R3 parallel zu R4
R3 ⋅ R 4
R rechts =
= 0,5 kΩ
R3  R 4
= 1,714 kΩ
//Variante 1
//Variante 2
rechter Teil:
Rges = 1,167 kΩ
Rges = 2,589 kΩ
b)
//Variante 1
//Variante 2
//Variante 1
//Variante 2
linker Teil unten:
R4 + R5 parallel zu R3
 R 4  R 5 ⋅ R 3
R links−unten =
= 0,667 kΩ
 R 4  R5   R3
= 2,25 kΩ
//Variante 1
//Variante 2
linker Teil :
R2 + Rlinks-unten parallel zu R1
 R 2  R links−unten ⋅ R 1
R links =
= 0,625 kΩ
 R 2  R links−unten   R 1
= 0,810 kΩ
//Variante 1
rechter Teil: alle vier Widerstände parallel
1
R rechts =
1
1
1
1
= 0,25 kΩ



R6
R7
R8 R 9
= 1,833 kΩ
//Variante 1
Rges = 0,875 kΩ
Rges = 2,643 kΩ
//Variante 1
//Variante 2
//Variante 2
//Variante 2
Bernd Sumpf
Eichberg1 • 07987 Reudnitz
03661/435814 • [email protected]
3.)
1
4
6
11
2
5
7
12
8
3
9
10
R1/2 = 50
R3/4 = 50
R6/7 = 50
R3 = 100
R8/9/10 = 150
R1-5 = 50
R6-10 = 37,5
R11/12 = 50
Rges = 137,5 Ω
4.)
Mit insgesamt 30 Widerständen:
10 parallele Widerstände ergeben 100 Ω;
20 parallele Widerstände ergeben 50 Ω; beides in Reihe sind 150 Ω
Mit insgesamt 16 Widerständen:
ergibt 0,6 kΩ; davon vier Einheiten parallel - fertig
Mit insgesamt 14 Widerständen:
R ges =
Es geht mit noch weniger !!!
1
1
1 1
⋅2   ⋅5
1,5
3 1