apl. Prof. Dr. D. Horstmann SS 2012 Dipl.

apl. Prof. Dr. D. Horstmann
Dipl.-Math. Hella Timmermann
SS 2012
6. Übung zur Vorlesung
Mathematik II für Studierende der Biologie“
”
Abgabe der schriftlichen Aufgaben am Montag, dem 4.6.12, bzw. am Dienstag,
dem 5.6.12, jeweils in den Übungen.
1. Aufgabe (schriftlich): Handelt es sich bei den folgenden Funktionen um Wahrscheinlichkeitsdichten einer
stetigen Zufallsvariablen? Begründen Sie Ihre Entscheidung!
(a) f1 (x) = 1
(
xe−x für x ≥ 0
(b) f2 (x) =
0
für x < 0


für − ∞ ≤ x < a
0
1
(c) f3 (x) = a−b
für a ≤ x < b


0
für b ≤ x
(
xe−x für x ≥ 0
(d) f4 (x) =
0
für x < 0
(
0
für x < 1
(e) f5 (x) = 7+x8
für
x≥1
x8
(
0
für x < 1
(f) f6 (x) = 7
für x ≥ 1
x8
9 Punkte
2. Aufgabe (schriftlich): Eine Bakterienpopulation wird zum Zeitpunkt t = 1 mit einem Gift kontaminiert. Die
Zufallsvairable X beschreibe den Zeitpunkt, zu dem ein Organismus nach der Kontaminierung stirbt, wobei die
zugehörige Dichtefunktion gegeben sei durch
(
2
für t ≥ 1,
3
f (t) = t
0 für t < 1.
(a) Berechnen Sie die Wahrscheinlichkeit, dass ein Organismus zum Zeitpunkt t = 5 noch lebt.
(b) Berechnen Sie die Wahrscheinlichkeit, dass die Überlebenszeit des Organismus nach der Kontaminierung 1
bis 5 Zeiteinheiten beträgt.
(c) Skizzieren Sie die Dichtefunktion f (t) und die in Teil (a) und (b) berechneten Wahrscheinlichkeiten.
6 Punkte
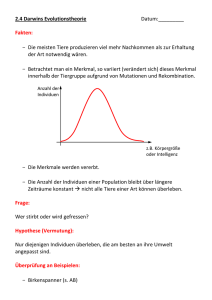
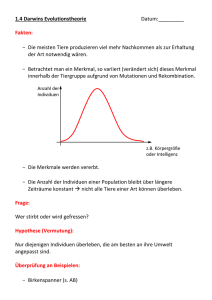
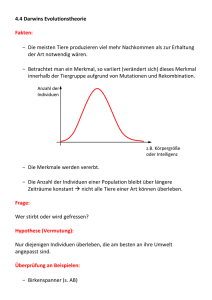
Die hypergeometrische Verteilung
Nehmen wir an wir haben N Objekte (zum Beispiel Kolbenhubpipetten) gegeben, wobei insgesamt m Stück
dieser Objekte ein besonderes Merkmal haben (z.B einen Fehler). Diese speziellen Objekte, die ein zu den
anderen Objekten abweichendes Merkmal aufweisen, bilden demnach einen Anteil von p = m
N der Gesamtmenge.
Nacheinander werden jetzt n Objekte ausgewählt, die jeweils nach ihrer Prüfung wieder zurück gelegt werden.
Auf diese Weise erhält man für die Wahrscheinlichkeit, dass x fehlerhafte Teile auftreten den Wert
n
(1 − p)n−x px .
x
Anders ist es jedoch, wenn man die n Teile nicht zurücklegt. In diesem Fall kann die Wahrscheinlichkeit, x
fehlerhafte Teile zu finden durch
m
N −m
x
n−x
P (X = x) =
N
n
ermittelt werden. Abstrakt läßt sich das wie folgt zusammenfassen:
Die Zufallsvariable X bezeichne die Anzahl der aus einer Menge M gezogenen Objekte vom Typ A bei der
zufälligen Ziehung (ohne Zurücklegen) von n Kombinationen aus M . Mit E = {X = x} sei das Ereignis bezeichnet, das alle möglichen Kombinationen von n vielen Objekten umfasst, die aus insgesamt x Objekten vom
Typ A und (n − x) Objekten eines anderen Typs bestehen. Insgesamt seien m Objekte vom Typ A und N − m
Objekte eines anderen Typs vorhanden. Die Wahrscheinlichkeit des Ereignisses E ist dann durch
m
N −m
x
n−x
P (X = x) =
N
n
gegeben. Eine derartige Zufallsvariable wird als hypergeometrisch verteilt mit Parametern N, n und p =
bezeichnet.
m
N
3. Aufgabe (schriftlich): Rückfangmethoden werden angewendet, um die Größe N einer Population zu schätzen.
Im einfachsten Fall werden aus der Population M Individuen eingefangen, markiert und wieder freigelassen.
Nachdem sich die markierten Individuen mit der übrigen Population vermischt haben, wird eine zweite Stichprobe von n Individuen entnommen und festgestellt, wie groß die Anzahl m der darunter befindlichen markierten
Individuen ist. Man schätzt nun die Größe N der Population indem man davon ausgeht, dass der Anteil der
markierten Individuen in der zweiten Stichprobe etwa dem Anteil aller markierten Individuen an der Gesamtpopulation entspricht, also
m
M
≈ .
N
n
(a) Nehmen Sie nun an, dass Sie bei der ersten Stichprobe 100 Individuen gefangen habe. Bei der zweiten
Stichprobe fangen Sie 20 Individuen, von denen 4 markiert sind. Wie groß schätzen Sie aufgrund dieser
Daten die Gesamtpopulation ein?
Nehmen Sie nun an, dass die Population aus 500 Individuen bestehe, von denen 100 markiert seien. Bei Ihrer
zweiten Stichprobe fangen Sie 20 Individuen ein.
(b) Wie groß ist die Wahrscheinlichkeit, dass Sie bei der zweiten Stichprobe genau 4 markierte Individuen
fangen und Ihre Schätzung für N tatsächlich exakt ist?
(c) Wir groß ist die Wahrscheinlichkeit, dass Sie bei der zweiten Stichprobe 3,4 oder 5 markierte Individuen
fangen?
5 Punkte
Die folgenden Aufgaben sind mündlich zu bearbeiten und werden in den an die jeweiligen
Übungen anschließenden Tutorien besprochen.
4. Aufgabe (mündlich): Im Rahmen einer Studie ist geplant, die auf einer Untersuchungsfläche befindlichen
Eintagsfliegenlarven zu zählen. Wie groß ist die Wahrscheinlichkeit, dass auf dieser Fläche mehr als sechs Larven gezählt werden, wenn die Anzahl X der Larven auf dieser Untersuchungsfläche der folgenden (diskreten)
Wahrscheinlichkeitsverteilung folgt:
λx e−λ
mit λ = 4.
x!
Eine solche Verteilung nennt man Poisson-Verteilung mit Erwartungswert 4.
P (X = x) =
5. Aufgabe (mündlich): Eine Kohorte von eurasischen Zwergmäusen wurde bezüglich ihres Gewichts untersucht.
Dabei ergab sich folgende Dichtefunktion:

0
für x ≤ 5



1x − 5
für 5 ≤ x ≤ 7
f (x) = 3 2 3 16

x
+
für 7 ≤ x ≤ 8
−

3

 3
0
für x ≥ 8
Skizzieren Sie die Dichtefunktion und begründen Sie, warum es sich tatsächlich um eine Dichtefunktion handelt.
Wie groß ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Maus zwischen 17/3 und 23/3 wiegt?
6. Aufgabe (mündlich): Betrachten Sie erneut die Funktion f3 (t) aus Aufgabe 1. Können Sie eine leicht modifizierte Funktion finden, die eine Dichtefunktion einer stetigen Zufallsvariablen ist?