13_ Ausbreitung_ des_ Lichts

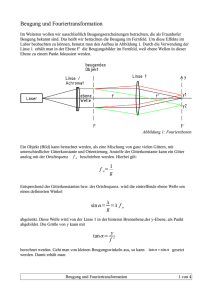
13 Ausbreitung des Lichts
13.1
Hofer
Bestimmung der Lichtgeschwindigkeit
13.1.1 Bestimmung durch astronomische Beobachtung
Olaf Römer führte 1676 die erste Berechung zur Bestimmung der Lichtgeschwindigkeit
durch.
Römer beobachtet dazu das Verschwinden eines Jupitermondes im Schatten des Jupiters.
In der Nahstellung des Jupiters zur Erde bestimmte Römer die Zeit zwischen zwei
Verfinsterungen des Jupitermondes zu 42,5h. Nach 103 Verfinsterungen (ungefähr ein
Jahr später) sollte die 104. Verfinsterung nach 103.42,5h eintreten. Tatsächlich trat die
Verfinsterung aber erst eine Viertelstunde später als erwartet ein!
Abb1: Bestimmung der Lichtgeschwindigkeit nach Römer
A1:
Erarbeite anhand der Skizze und den obigen Angaben, wie Römer die
Lichtgeschwindigkeit bestimmt hat!
13.1.2 Bestimmung der Lichtgeschwindigkeit anhand der Zahnradmethode
Erst 180 Jahre später ist es gelungen die Lichtgeschwindigkeit auf der Erde zu messen!
Fizeau hat im 19. Jhdt. mit Hilfe eines Zahnrads die Lichtgeschwindigkeit bestimmt.
Abb2: Versuchsaufbau der Zahnradmethode von Fizeau
1
13 Ausbreitung des Lichts
Hofer
Zunächst versetzte man das Zahnrad in Rotation. Während des Zunehmens der
Rotationsgeschwindigkeit stellte man eine Abschwächung der Lichtintensität des reflektierten
Lichtstrahls fest. Dies erklärt sich dadurch, dass der reflektierte Strahl auf den folgenden Zahn
des rotierenden Zahnrades trifft. Bei einer weiteren Erhöhung der Rotationsgeschwindigkeit
trat wieder ein Maximum an Helligkeit ein, weil der reflektierte Strahl durch die nächste
Zahnlücke treten konnte.
Aus der Zeit t, in der eine Lücke der nächsten Lücke folgte, und aus der Entfernung s des
Spiegels vom Zahnrad errechnet sich die Lichtgeschwindigkeit:
c0 =
2.s
t
c0…Lichtgeschwindigkeit
2.s…Weg für Hin- und Hergang
t…Zeit für Hin- und Hergang
(Aus der Zahl n der Umdrehungen pro Sekunde des Zahnrades und der Anzahl z der Zähne
1
des Zahnrades folgt: t =
)
n.z
A1:
Berechne die Umdrehungszahl des Zahnrades vom Fizeau (720 Zähne), wenn bei
Erhöhung der Rotation das erste Mal ein Helligkeitsminimum auftritt.
A2:
Wie lange dauert es, bis ein Lichtstrahl, der von der Erde ausgesendet und am Mond
reflektiert wird, wieder auf die Erde eintrifft? (Mond – Erde: 380 000km)
A3:
Berechne, wie lange das Licht von der Sonne zur Erde braucht!
Können Astronomen beobachten, was sich im Universum ereignet?
A4:
Welcher Wert ergibt sich, wenn man folgende von Fizeau gemessenen Zahlenwerte
einsetzt?
s = 8 633m, z = 720, n = 12,6 Umdrehungen/s
2
Hofer
13 Ausbreitung des Lichts
13.2
Strahlengang durch optische Bauelemente
Die planparallel Platte
A1:
Zeichne den Strahlengang durch eine planparallele Platte!
Abb.2:Planparallele Platte
Das Prisma
A2:
Zeichne Strahlegang durch ein Prisma!
Abb.2: Prisma
Die Sammellinse
Abb.3: Strahlengang einer Sammellinse
3
Hofer
13 Ausbreitung des Lichts
Rechnerisch lassen sich die Lage und die Größe des Bildes folgendermaßen finden:
Aus der Abb.3 ergeben sich folgende Vergrößerungsverhältnisse:
B b
=
G g
B…Bildgröße
G…Gegenstandsgröße
b…Bildweite
g…Gegenstandsweite
A3:
Leite aus geometrischen Überlegungen die Linsengleichung her!
Linsengleichung
1 1 1
= +
f g b
f…Brennweite
g…Gegenstandsweite
b…Bildweite
A4:
Konstruiere Abbildungen eines Gegenstandes mit einer Sammellinse mit folgenden
Vorgaben:
a
g=f
b
f < g < 2f
c
g > 2f
d
g<f
4
13 Ausbreitung des Lichts
Hofer
5
Die Zerstreuungslinse
Abb4: Zerstreuungslinse
A5:
Versuche die Abbildung zu erklären!
Zerstreuungslinsen sind in der Mitte dünner als am Rand. (Konkavlinsen).
Lichtstrahlen werden durch die Zerstreuungslinse divergent gemacht.
Für die Abbildung durch Zerstreuungslinsen gelten dieselben Konstruktionsverfahren wie für
Sammellinsen. Die Brennweite f ist negativ. Es gilt dann ebenfalls die Linsengleichung.
Die Bilder, die durch Zerstreuungslinsen erzeugt werden, sind stets verkleinert und aufrecht
und nicht auf einem Schirm auffangbar. (Virtuelle Bilder)
Abb5: Entstehung von einem Bild bei einer Zerstreuungslinse
1
; [f] = m
f
Welche Linsen sind in einer Brille mit D = - 2 dpt
Die Brechkraft einer Linse ist definiert:
A6:
D=
D…Dioptrie, f…Brennweite
13 Ausbreitung des Lichts
A7:
Hofer
Konstruiere mit Hilfe der Schülerversuchsbaukästen ein Mikroskop!
Beschreibe und skizziere den Versuch!
Einige Linsenfehler:
Sphärische Aberration
Sie zeigt sich dadurch, dass nicht alle auf eine Linse großer Öffnung fallenden
achsenparallelen Strahlen in einem Brennpunkt vereinigt werden. Die Randstrahlen
ergeben eine kürzere Brennweite.
A8:
Konstruiere diesen Linsenfehler!
A9:
Wie könnte man den Linsenfehlerausgleichen?
Astigmatismus ( Punktlosigkeit )
Wird eine Linse von einer Fläche mit verschiedenen Krümmungen begrenzt oder werden
Punkte abgebildet die weit außerhalb der optischen Achse liegen, dann vereinigen sich die
parallelen Lichtbündel nicht in einem Brennpunkt, sondern in zwei Geraden mit
verschiedenem Abstand von der Linse.
Abb.6:Astigmatismus
Chromatische Aberration
Infolge verschiedener Brechzahlen des Glases für verschiedene Lichtfrequenzen (Dispersion)
liegt der Brennpunkt für die stärker gebrochenen violetten Strahlen näher an der Linse als für
die roten Strahlen.
A10: Beschreibe die Gründe der Kurz- und Weitsichtigkeit des menschlichen Auges!
6
13 Ausbreitung des Lichts
Hofer
13.3 Beugung(difracción (la), Streuung(dispersión, la) und Interferenz(interferencia
(la) ) von Wellen
13.3.1 Beugung und Streuung
A1:
Wiederhole die Begriffe Wellenlänge, Interferenz und Elementarwelle!
Beugung:
Beugung ist der Eintritt einer Welle in den geometrischen Schattenraum! (λ ≈ d)
A2:
Zeichne die Beugung einer Wasserwelle an einem Spalt!
A3:
Wo kommt Beugung im Alltag vor?
A4:
Warum kann man Beugung von Licht im Alltag nicht beobachten!
Streuung
Abb.1:Streuung
Erreicht eine Wellenfront ein Hindernis, so gehen vom Hindernis selbst Elementarwellen aus,
die sich in allen Richtungen ausbreiten. Dieser Effekt wird allgemein als Streuung genannt.
Interferenz, Überlagerung
A5:
Zeichne zwei Wellen gleicher Wellenlänge und gleicher Schwingungsrichtung mit der
oben angegebenen Bedingung!
Zeichne die resultierende Welle ein!
A6:
Beobachte die Überlagerung zweier Kreiswellen mithilfe eines entsprechenden JavaApplets!
7
13 Ausbreitung des Lichts
Hofer
Zeigt ein Phänomen Beugungs- und Interferenzerscheinungen, so kann dieses
Phänomen durch das Wellenmodell beschrieben werden.
13.4 Interferenz an dünnen Schichten
Damit Interferenz zwischen Lichtquellen beobachtet werden kann, müssen sie zumindest
gleiche Frequenz und gleich bleibende Phasenunterschied aufweisen und das gleiche
Raumgebiet durchlaufen. Solche Lichtwellen heißen kohärent.
Abb1: Interferenzerscheinungen an dünnen Schichten
Die benachbarten Wellenzüge weisen Laufzeitunterschiede auf. Je nach Reflexion am
dichteren oder dünneren Medium tritt ein Phasensprung auf.
Daraus ergibt sich Verstärkung oder Auslöschung der Lichtwellen.
A1:
Beschreibe und begründe die Laufzeitunterschiede in der Abb.1!
A2:
Nenne Bespiele wo man im Alltag Interferenzerscheinungen des Lichts beobachten
kann!
Anwendung: Vergütung von Linsen
Abb2: Vergütung von einer Linse
Durch die das Aufbringen einer zusätzlichen Schicht mit kleiner optischer Dichte als
die Linse interferiert das Reflexionslicht destruktiv. Das in die Linse eintretende Licht
wird verstärkt. Je nach erwünschter Auslöschung wählt man die Schichtdicke
d=
λ
4n
.
8
13 Ausbreitung des Lichts
Hofer
13.5 Beugung(difracción (la))
13.5.1 Beugung am Doppelspalt
Versuch:
Ein Laserstrahl fällt durch einen Doppelspalt.
A1:
Skizziere den Versuch und beschreibe das Versuch Ergebnis!
Wie entsteht das Beugungsbild?
Abb.1:Beugung am Doppelspalt
A2:
Überlege, mithilfe der obigen Abbildung wie es das Beugungsmuster entsteht und
leite die entsprechende Formel her!
9
Hofer
13 Ausbreitung des Lichts
13.5.2
Beugung am Gitter
Ein optisches Gitter besteht aus vielen gleich breiten Einzelspalten. Der Abstand d der
Spalten ist immer gleich. Der Abstand zwischen den benachbarten Spalten wird
Gitterkonstante d genannt.
Zur Erklärung der Beugung am Gitter gilt die gleiche Überlegung wie beim Doppelspalt.
sin ϕ =
nλ
d
n...beschreibt das n-te Beugungsmaximum
λ…Wellenlänge
d…Abstand zwischen den benachbarten Spalten
θ…Winkel zum n-ten Hauptmaximum
Abb.1:
Beugung am optischen Gitter
13.5.3 Bestimmung der Lichtwellenlänge
V:
Wir verwenden ein Gitter mit bekannter Gitterkonstante. Wir lassen den Lichtstrahl
das Gitter passieren. Wir messen den Abstand L des Schirms vom Gitter und den
Abstand D des ersten Hauptmaximums vom Zentralbild. Daraus kann man λ
berechnen.
10