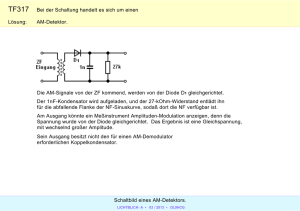
UniversitätÈOsnabrück Vorlesung Elektronik W. Bodenberger

Universität Osnabrück
Fachbereich Physik
Dr. W. Bodenberger
Vorlesung Elektronik W. Bodenberger
1
Stabilisierung von Gleichspannungen mit einer Diode
Stabilisierung von Gleichspannungen
R
U
Der Diodenstrom iD und die Diodenspannung U2 sind durch zwei
Bedingungen festgelegt:
1)durch die Diodenkennlinie iD = f(U2 )
2)durch die Eingangsspannung U1 und den Spannungsabfall von
iD + iL an RL
i
1
i
i
D
L
R
U
L
2
Mit den Kirchhoffschen Regeln ergibt sich:
KSR:
i − iD − iL = 0
(1)
KVR:
i · R + U2 − U1 = 0
Der Spannungsabfall am Lastwiderstand RL ergibt sich zu
U2
iL =
RL
Aus (2) erhält man:
U1 − U2
i=
und aus (1) iD = i − iL
R
Ersetzt man die Ströme i und iL durch die Spannungen so ergibt sich
(2)
(3)
(4)
U1 − U2 U2
(5)
−
R
RL
Dies ist die Geradengleichung der Arbeitsgerade oder auch Widerstandsgerade, die man im Kennlinienfeld iD undU2 darstellt.
iD =
1
U1
1
− U2 · ( +
)
(6)
R
R RL
Den Achsenabschnitt auf der y - Achse erhält man, wenn
man U2 = 0 setzt. Dies ergibt den maximalen Strom der
durch die Diode fließt. Er ist gleich U1 /R. Die maximale
Ausgangsspannung U2max (den Achsenabschnitt auf der x Achse) erhält man, wenn man den Strom iD = 0 setzt.
Er ist:
(R+R )
RL ·U1
U2 = (R+R
. Die Steigung ist − R·RLL
L)
Die gesuchte Ausgangsspannung U20 im Arbeitspunkt ergibt sich aus dem Schnittpunkt beider Kurven im iD − U2 Diagramm.
iD =
i
D
A rb e its g e ra d e
K e n n lin ie
i
A rb e its p u n k t
D 0
U
2 0
D io d e n k e n n lin ie m it A rb e its g e ra d e
U
2
Universität Osnabrück
Vorlesung Elektronik W. Bodenberger
2
Eine Änderung ∆U2 von U20 kann zwei Ursachen haben, einmal ein Schwanken der Primärspannung
um ∆U1 . Zum anderen eine Änderung der Belastung RL , d. h. Änderung des Verbraucherstromes
um ∆iL .
1
Im ersten Fall wird die Widerstandsgerade um ∆U
R parallel verschoben:
i
D
,
A rb e its g e ra d e
Aus dem Bild liest man ab:
∆U2 = rD · ∆iD
Für ∆iD kann man die Widerstandsgerade einsetzen:
∆U1 ∆U2 · (R + RL )
∆U2 = rD ·
−
R
R · RL
K e n n lin ie
A rb e its p u n k t
i
D 0
, U
U
2
(7)
Für die Ausgangsschwankung ∆U2 in Abhängigkeit von der
Schwankung der Eingangsspannung U1 ergibt sich dann:
⎛
⎞
∆U1
rD
⎠
(8)
∆U2 = ⎝
R 1 + rD ·(R+RL )
2
D io d e n k e n n lin ie m it A rb e its g e ra d e b e i
S c h w a n k u n g d e r E in g a n g s s p a n n u n g U R·RL
Ist rD R·RL
(R+RL )
dann wird
rD
(9)
· ∆U1
R
Ändert sich die Belastung um ∆iL , so dreht sich die Widerstandsgerade um den Schnittpunkt
der iD - Achse:
∆U2 =
i
D
mit
,
2
Mit i = U1 −U
erhält man da U1 konstant sein soll
R
∆U2
für ∆i = − R . Für die Ströme gilt nach Formel (1)
∆iD = ∆i − ∆iL
Damit ∆U2 = rD · ∆iD = rD · [∆i − ∆iL ].
Die Auflösung nach ∆U2 und ∆iL ergibt:
K e n n lin ie
A rb e its g e ra d e
i
U1
R
A rb e its p u n k t
D 0
, U
2
D io d e n k e n n lin ie m it A rb e its g e ra d e b e i
S c h w a n k u n g d e r B e la s tu n g
U
2
∆U2 =
R · rd
· ∆iL
(R + RL )
(10)
Für rD R wird damit aus der vorstehenden Gleichung:
∆U2 ≈ rD · iL
(11)
Das bedeutet, die Spannungsquelle hat effektiv einen Innenwiderstand der Größe rD . Das ursprüngliche Schaltbild wird damit äquivalent zu einer Ersatzspannungsquelle mit einem Innenwiderstand, der
aus der Parallelschaltung des Diodenwiderstandes rD und dem Begrenzungswiderstand R besteht.
Universität Osnabrück
U
Vorlesung Elektronik W. Bodenberger
1
r
R L
U
D
R
2 0
U
3
R L
U
2
2 0
Zahlenbeispiel: Als Beispiel wird eine Si - Diode gewählt.
Die Werte im Arbeitspunkt sind:
iD0 = 40mA U20 = 0, 8Volt
rD = 1Ω
U1 = 10Volt RL = ∞
Am Widerstand R muß die Restspannung von U1 minus dem Spannungsabfall an der Diode U20 abfallen.Damit erhält man für R:
R=
U1 −U20
iD0
=
9,2
4
· 102 = 230Ω
Wie groß ist nun die Stabilisierung gegen Schwankungen der Eingangsspannung U1 ?
∆U2
∆U1
oder
= 4 · 10−3
rD
R
=
1
230
∆U2
U20
=
∆U2 ∆U1 U1
∆U1 · U1 · U20
=
1
= 5 · 10−2 · ∆U
U1 .
Welche Stabilisierung erreicht man bei einer Schwankung des Lastwiderstandes RL ?
∆U2 = rD · ∆iL
Bei einer angenommenen Schwankung von ∆iL von 10 mA ergibt sich eine Schwankung der Ausgangsspannung von ∆U2 = 1 · 10−2Volt.
Universität Osnabrück
Vorlesung Elektronik W. Bodenberger
4
Stabilisierung mit Zenerdiode.
Genau das gleiche Prinzip der Spannungsstabilisierung durch eine in Durchlaßrichtung betriebene
Diode wird angewendet bei einer Stabilisierung durch eine in Sperrichtung betriebene Zenerdiode:
U
2
U
Z
= Z e n e rd u rc h b ru c h sp a n n u n g
A rb e its g e ra d e
U
1
R L
U
2 0
D u rc h b ru c h k e n n lin ie e in e r Z e n e rd io d e
U
iZ
A rb e its g e ra d e u n d K e n n lin ie n fe ld e in e r
Z e n e r - D io d e
Spannungsbegrenzung nach unten (pick - off - Diode.
R
1
+ U d
U 2
0
U
+ U d
1
0
Im p u ls h ö h e n - D irk rim in a to r
Die Grundschaltung ist sehr einfach. Sie besteht
aus einer Diode und einem begrenzenden Widerstand R an den in diesem Fall eine positive
Spannung +Ud angelegt ist. So lange die Eingangsamplitude von U1 kleiner als die von Ud ist bleibt
die Diode gesperrt und U2 ist gleich Null.
Die nebenstehende Schaltung ist die einfachste
Form eines Impulshöhen Diskriminators. Impulse,deren Amplituden kleiner als Ud sind werden
nicht übertragen.
Universität Osnabrück
Vorlesung Elektronik W. Bodenberger
5
Erzeugung von Dreiecks - Impulsen.
Mittels eines RC - Hochpasses einer Diode und einer Klemmspannung lassen sich Dreieckspulse erzeugen.
Bei t= 0 springt U2 auf
die Spannung U. Dadurch
wird die Diode gesperrt.U2
strebt nach dem Sprung
zunächst exponentiell gegen
−Ud ,solange die Diode
sperrt, d.h. U2 > 0 ist:
C
U 2
U
U
0
R
1
U
0 V o lt
t = 0
t = 0
- U d
-U d
U2 = (U + Ud ) · exp( −t
T ) − Ud für U2 ≥ 0
U2 ≈ U − (U + Ud ) · Tt für t T
t
wenn u Ud
U2 ≈ U − Ud · R·C
Sobald jedoch U2 Erdpotential erreicht, leitet die Diode wieder und hält U2 auf dem Potential 0 fest.
Ist Ud U so nimmt U2 annähernd linear ab, und es entsteht ein Dreieckspuls mit der Basisbreite
τ ≈ T · UUd
Impulsverlängerung mit pick - off - Dioden.
Die Schaltung besteht im Prinzip aus einem Tiefpaß mit einer Diode in Serie.
R d
R
J
U
i
C
R
U 2
J
T 2 = R C
1
U2 wächst nach dem positiven Sprung von U1 exponentiell mit T1 = (Ri + Rd ) · C an.
Springt U1 zurück auf 0 Volt, sperrt die Diode und der Kondensator entlädt sich mit T2 = R · C über
R.