Gleichstromkreise

Gleichstromkreise
Vom einfachen Modell zu anspruchsvollen Fragen
a) Eine Modellbetrachtung zum Verständnis von Stromstärke und Spannung
b) Ein einfaches Grundgesetz mit zugehörigen Regeln´: Das Ohmsche Gesetz
c) Die Vielfalt der so folgenden determinierten Sachverhalte
d) Textinterpretation und Problematik Regel-Beispiel
• Stromstärke (in einem Leitungsquerschnitt) - Modellinterpretation: Flüssigkeitsmenge, die pro Sekunde
den Querschnitt passiert. Konstant, solange keine Flüssigkeit verloren geht, hinzukommt oder eine
Verzweigung auftritt.
• Spannung (zwischen zwei Leitungspunkten) - Modellinterpretation: Höhenunterschied im Wasserlauf
zwischen den zwei Punkten.
Ein " unphysikalischer Stromkreis"
Atomistische Interpretation:
• Stromstärke ist die pro Zeiteinheit den Querschnitt passierende Elektrizitätsmenge
• Spannung: Die an einer Masse, die von im Schwerefeld von A nach B transportiert wird, zu leistende
Arbeit ist proportional zum Höhenunterschied der beiden Punkte! Entsprechend ist die Arbeit, die
man an einer elektrischen Ladung leisten muss, um sie von A nach B zu transportieren,
proportional zur Potentialdifferenz und das ist die Spannung!
Modellinterpretation der beiden Grundstromkreise:
Die Reihenschaltung:
1
Die Parallelschaltung:
• Die Ausgestaltung der jeweiligen Gefällestrecke bzw. Röhre bestimmt die Beziehung zwischen Stromstärke und Höhendifferenz (Spannung). Im elektrischen Fall wird diese Beziehung gegeben durch das
Ohmsche Gesetz:
I=
1
RU
Eine angel. Spannung U bewirkt einen Strom der Stärke I
R eine Konfigurationskonstante. Genauer: ¤..
Diese Beziehung wird experimentell bestätigt!
¤ Die Spannung sei an einem homogenen Draht der Länge L und mit Querschnit A angelegt. Was ist
dann für R zu erwarten? Wie sollte die physikalische Analyse in Bezug auf R weitergehen?
•
Zum Zweck der gedanklichen Verarbeitung arbeitet man mit idealisierten Schaltungen. Für diese leitet
man die Vielzahl der Folgerungen her, die man dann mit der REalität vergleicht.:
2
•
— Eine solche idealisierte Schaltung besteht aus verlustfreien Leitungen und in einzelnen Widerständen lokalisierten Verluste. Über jedem Widerstand gilt das Ohmsche Gesetz mit zugehörigem
spezifischen R-Wert. .
— Diese Bestandteile werden situationspezifisch (irgendwie sinnvoll) zusamengeschaltet
— Eine Spannung wird eingebaut
— Das verursacht (determiniert) in jeder Leitung einen ganz bestimmten Stromfluss - zusammenfassbar in einem Stromvektor I.
• Darstellung in einer Schaltskizze
• Die beiden Kirchhoffschen Regeln: ¤ ...Formulierung.....
• Was ist daher alles in einer solchen Schaltung messbar?
• Zielperspektive
— Erfahrung sagt: I ist eindeutig bestimmt durch.die ideale Konfiguration..
— Problem: Vorhersage von I mit Hilfe der Konfiguration.
• Anwendung der Kirchhoffschen Regeln gibt lineares Gleichungssystem für I . U gehört zum Inhomogenitätenvektor.
• Behandlung und Lösung in der Mathematik . Resultat: Tatsächlich immer eindeutig lösbar! Formal:
Lösungsvektor I (Mathematisch berechnet und parallel physik. determiniert)
Dieses einfache Konzept - also hauptsächlich die beiden Kirchhoffschen Regeln - bestimmen,
determinieren jetzt eine unglaubliche Vielzahl nachprüfbarer Sachverhalte. Zunächst einmal
für jede einzelne Schaltung und dann für die Veilzahl möglicher Schaltungen.
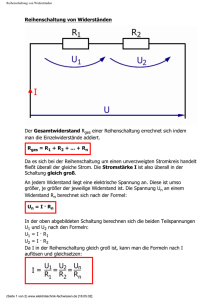
Die erste Grundschaltung: Reihenschaltung von Widerständen :
I1
I2
R1
R2
H1
H2
z }| { z }| {
R1 I1 + R2 I2 = U
I1 = I2
(R1 + R2 )I1 = U
R = R1 + R2
I1 = I2 = R1 U
+R2
U
1
I= R1 +R
2
µ
1
1
¶
U
RGesamt = R1 + R2
Die zweite Grundschaltung: Parallelschaltung von Widerständen
I1
R1
I0
R2
I2
I0 − I1 − I2 = 0
R1 I1 − R2 I2 = 0
R1 I1 = U
U
3
I1 = RU1
I2 = ³RU2
I0 = R11 +
1
R2
´
U
Die Lösung erfolgt über Inspektion. (Ende der Elimination, Rückeinsetzen)
Aus dem Resultat abstrahiert man (rekursiv) die übliche
Regel für Parallelschaltung von Widerständen!
⎞ ⎛
I0
I=⎝ I1 ⎠=⎝
I2
⎛
¤ I0 = 3A, I2 = 1A U=100V
R1 R2
R1 +R2
1
R1
1
R2
⎞
⎠U
R2
RGesamt = RR11+R
2
1
1
1
RGesamt = R1 + R2
Wie groß sind R1 , R2 ?
3. Beispiel!
Das Gleichungssystem lautet:
⎡
I1
⎣ R1 I1
R1 I1
−I2
+R2 I2
+0
¤ Wie sieht die Schaltskizze aus?
Lösen des Gleichungssystems:
∙
(R3 + R1 )I1
R1 I1
⎤
=0
R3 (1)+(3)
= U ⎦ (2)
I3 raus
=U
−I3
+0
+R3 I3
−R3 I2
+R2 I2
=U
=U
¸
R2 (1) + R3 (2)
[(R2 R3 + R1 R2 + R1 R3 ) I1 = (R2 + R3 )U ]
Rückeinsetzen
R2 +R3
I1 = R2 R3 +R
U= ³
1 (R2 +R3 )
R2 I2
= U − R1 ³
R1 +
U
R2 R3
R2 +R3
=
I3
=
I2 =
2
´ = U − R1
3
U (R2 + R3 )
R1 R2 + R1 R3 + R2 R3
R2 R3
R1 R2 + R1 R3 + R2 R3
R2 R3
R3
U
=
U
R1 R2 + R1 R3 + R2 R3 R2
R1 R2 + R1 R3 + R2 R3
R2
U
R1 R2 + R1 R3 + R2 R3
= U
I2
1
´U
R R
R1 + R 2+R3
R3
R1 R2 +R1 R3 +R2 R3 U
I3 =
R2
R1 R2 +R1 R3 +R2 R3 U
Vektoriell geschriebenes Resultat:
I= R1 R2 +R1UR3 +R2 R3
¤ Was ist hier RGesamt ??
⎛
⎞
1
R2 + R3
R1 R2 +R1 R3 +R2 R3
⎝
⎠ = U·
R3
R2
4
⎛
⎞
R2 + R3
⎝
⎠
R3
R2
4. Beispiel
I2
R2
R1
I1
R3
I3
U
⎡
⎣
I1
−I2
+0
+(R1 + R2 )I2
0
⎤
=0
=U ⎦
=U
−I3
+R3 I3
+0
1
1
U
I2 =
U
R3
R1 + R2
µ
¶
1
1
R1 + R2 + R3
+
+
U=
U
I1 =
R1 + R2 R3
R3 (R1 + R2 )
⎛
⎞
R1 + R2 + R3
⎠U
R3
I = R3 (R11 +R2 ) ⎝
R1 + R2
Benötigt wird vielfach nur ein Teil RGesamt I1 = U
I3
=
RGesamt =
R3 (R1 + R2 )
=
R1 + R2 + R3
1
1
R1 +R2
+
1
R3
Tests? R3 = 0 / R1 = ∞ R1 + R2 = 0....Z1 =
1
R1
5. Beispiel: Die Wheatstonesche Brücke
I4
R
2
R4
I2
R5
I0
R
3
R1
I1
I5
U
5
I3
+
1
R2 +R3
Ein 6×6−Satz möglicher Gleichungen lautet: (3mal 1. Kirchh. u. 3mal 2. Kirchh)
I0
−I1
−I2
I2 R2
I1 R1
−I0
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
−I1 R1
I0
I1
I2
I3
I4
I5
⎞
⎟
⎟
⎟
⎟=
⎟
⎟
⎠
I2
I2 R2
⎛
⎜
⎜
⎜
U ⎜
Det ⎜
⎜
⎝
1
−1 −1 0
0
0
=0
0
0
R2 0 R4 0
=U
0
R1
+I3 R3
=U
0 R3 0
0
0
0
1
0 −1 −1
−I4
−I5
=0
0 −R1 R2 0
+I5 R5 = 0
0 R5
I3
+I4
=0
−1
0
0
1
1
0
Gibt als Lösung:
⎞
R5 R2 + R3 R2 + R4 R2 + R5 R4 + R5 R3 + R5 R1 + R3 R1 + R4 R1
⎟
R5 R2 + R3 R2 + R4 R2 + R5 R4
⎟
⎟
R5 R3 + R5 R1 + R3 R1 + R4 R1
⎟
⎟
R5 R2 + R4 R2 + R5 R4 + R4 R1
⎟
⎠
R3 R2 + R5 R3 + R5 R1 + R3 R1
R1 R4 − R2 R3
0
+I4 R4
Det=R2 R3 R4 + R3 R4 R5 + R2 R3 R5 + R1 R2 R4 + R1 R4 R5 + R1 R2 R5 + R1 R3 R4 + R1 R2 R3
• Weiterverarbeitung:
— Spannungsabfälle, Leistung, "Ohmsches Gesetz"- RGesamt -Bestimmung
— Kurzschluss / Sperrfall
— Vereinfachte Regeln zur Bestimmung von RGesamt für rekursiv aus Parallel- und Reihenschaltung aufbaubare Schaltungen
— Experimentelle Prüfung
— Technische Anwendungen
— Verallgemeinerungen
6
Weiterführende Fragen:
¤ Wieviel unterschiedliche Schaltungen gibt es zu vorgegebener Anzahl von Widerständen?
¤ Wieviel davon kann man rekursiv durch Parallel- und Reihenschaltung aufbauene
7