Ideales Gasgesetz

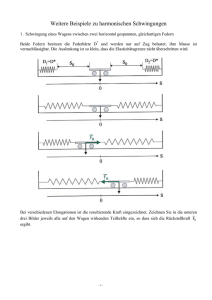
Schwingungen
Durch Federzüge, Gummis, Stahlstangen, Druckbehälter, Auftriebskräfte etc. kann es zu Hinund Herbewegungen kommen. Diese bezeichnet man als Schwingungen.
Einige Beispiele!
http://www.leifiphysik.de/mechanik/mechanische-schwingungen/mechanischeschwingungen-grundbegriffe
A) Räumliche Begrifflichkeiten
Beobachten wir Schwingungen, so beobachten wir neben zeitlichen Größen, die die
„Schnelligkeit“ einer Schwingung kennzeichnen, auch räumliche Begrifflichkeiten.
Betrachten wir dazu folgende Animation!
http://www.leifiphysik.de/mechanik/mechanische-schwingungen/bewegungsgleichungharmonische-schwingung
Die Bewegung könnte beispielsweise durch eine Feder hervorgerufen werden!
http://www.leifiphysik.de/mechanik/mechanische-schwingungen/kraftgesetz-harmonischeschwingung
1.) Ruhelage
Ein wenig paradox, die Bezeichnungsweise, besitzt doch der schwingende Punkt in der
Ruhelage die größte Geschwindigkeit!
(Möglicherweise stammt die Bezeichnung daher, dass wenn man den schwingenden Körper in
der Ruhelage loslässt, er in Ruhe bleibt.)
In der Ruhelage ist die Geschwindigkeit maximal und die Beschleunigung 0m/s2.
2.) Umkehrpunkte
An den Umkehrpunkten herrscht die Geschwindigkeit 0m/s. Die einwirkende Kraft auf den
Körper und damit die Beschleunigung ist maximal.
3.) Auslenkung
Die Auslenkung x(t) ist der Abstand zwischen Momentanposition und der Ruhelage.
4.) Amplitude
Ist die maximale Auslenkung
5.) Rücktreibende Kraft
Ein Blick auf die Animation zeigt auch, dass die rücktreibende Kraft immer der
Auslenkung gegengerichtet ist.
Steigt der Betrag der Auslenkung, so tut es auch die rücktreibende Kraft!
Das ist ja die Voraussetzung dafür, dass der Körper auf den Bereich zwischen den
Umkehrpunkten beschränkt ist!
Ein linearer Auslenkungs-Kraft-Zusammenhang lässt sich folgend formalisieren.
F(y) =−ky
Das bedeutet, dass der Betrag der rücktreibenden Kraft F linear mit dem Betrag der
Auslenkung y anwächst!
k (oder auch D) nennt man die Federhärte!
Ausführungen dazu siehe auch
http://www.leifiphysik.de/mechanik/kraft-und-das-gesetz-von-hooke/gesetz-von-hooke
1
B) Zeitliche Begrifflichkeiten
Für die Beschreibung von Schwingungen empfiehlt es sich, rotierende Zeiger zu verwenden.
Warum, wird in der folgenden Animation deutlich, welche die Zeit-Orts-Abhängigkeit
wiedergibt!
http://www.leifiphysik.de/mechanik/mechanische-schwingungen/bewegungsgleichungharmonische-schwingung
Der hellrote Punkt ist der Schatten des rotierenden Punktes und führt eine Schwingung aus.
So lässt sich eine Schwingung mit Hilfe eines rotierenden Punktes erklären!
Voraussetzung: lineares Kraftgesetz!
1.) Winkelgeschwindigkeit
Denken wir uns einen Zeiger vom Drehzentrum der Rotation zum rotierenden Punkt!
Der Zeiger dreht sich dann mit der sogenannten Winkelgeschwindigkeit, die folgendermaßen
definiert ist:


t
Δφ ist dabei der überstrichene Winkel im Radiantenmaß innerhalb einer Zeit Δt.
Bsp.: Vollführt der Zeiger innerhalb einer Zeit von 2s eine volle Drehung (2π im
Radiantenmaß) so beträgt Δφ/Δt=2π/2s=π/s.
2.) Schwingungsdauer
Unter der Schwingungsdauer versteht man die Zeit einer vollständigen Hin- und
Herschwingung.
Im Zeigermodell entspricht das einer vollen Drehung um 2π.
Somit: t  T  2 und daher
T  2

3.)Frequenz f
Die Frequenz f beschreibt die Anzahl der Hin- und Herschwingungen pro Zeit.
Also:
Anzahl der Hin  und Herschwingungen
f 
Zeit
oder
umgeformt
f  t  Anzahl der Hin  und Herschwingungen
Speziell: Innerhalb EINER Hin- und Herschwingung rotiert der Zeiger einmal.
Hier vergeht aber gerade genau die Periodendauer T!
Daher: f T  1
oder:
f 
1
T
2
C) Bedingungen für die Richtigkeit der Darstellung einer Schwingung mit Hilfe von
Zeigern
1.) Offensichtlich: Der Radius der Rotation muss der Amplitude (maximale Auslenkung) der
Schwingung entsprechen.
r=y0.
2.) Mitteilung ohne Herleitung
Die Winkelgeschwindigkeit des Zeigers der Rotation muss folgenden Betrag haben:

D
m
D..Federhärte des Systems; m…Masse des schwingenden Punktes
Der Gleichung entnimmt man: Offenbar rotiert der Zeiger dann schnell, wenn die Feder
sehr starr ist und die Masse, die schwingt, eher klein ist!
Eine netten Animation dazu findest Du unter
http://www.leifiphysik.de/mechanik/mechanische-schwingungen/versuche/federpendelsimulation-von-phet
3