feldstärke die

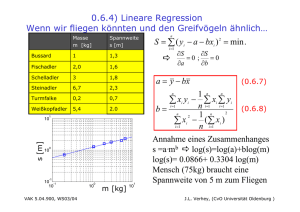
3. Elektrostatik (Motivation)
Nervenzelle
• 18 Jh.: Neurone wie elektrische Leiter.
• ABER: Widerstand des Axoplasmas sehr hoch
2,5 · 108 Ω (vergleichbar Holz)
• Weiterleitung durch Prozesse senkrecht zur
Zellmembran
• Zellmembran wie ein Kondensator
(Ruhepotential -60mV)
• Elektrochemische Prozesse wesentlich
• Zum Verständnis Grundbegriffe der
Elektrizitätslehre wichtig
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
3. Elektrostatik
• Elektrizität:
• ~ 600 v. Chr.: Reibung
eines Stabes z.B. aus
Bernstein (ểlektron griech.)
bewirkt Anziehung leichter
Körper.
Stab aus z.B.
Bernstein, Glas
(Hartgummi)
Lappen, z.B.
Katzenfell
(Wolllappen)
• Elektrostatik: Beschäftigt
sich mit ruhenden
Ladungen und ihren Feldern
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
3.1. Elektrische Ladung
• Es gibt positive & negative Ladungen
Lichtenbergfiguren
Positive Ladung
“Nimmt man nun
die Röhre mit der bloßen Hand fort und
streut Pulver auf die Scheibe, so wird eine
strahlende Sonne erscheinen”
(Lichtenberg)
G. C. Lichtenberg 1742-1799
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
3.1. Elektrische Ladung
• Gleichartige Ladungen stoßen sich ab.
-
-
+
+
• Ungleichartige Ladungen ziehen sich an.
+
-
• Ladungen können nicht erzeugt werden.
• Können in eine ursprünglich neutralen
Körper getrennt und umverteilt werden.
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
3.1. Elektrische Ladung
• Ladungserhaltung: In einem
abgeschlossenen System bleibt die Summe
aus positiven und negativen Ladungen
konstant.
• Ladung ist gequantelt, d.h. sie ist
ganzzahliges Vielfaches der
Elementarladung
e0=1,602176·10-19 C (Coulomb)
(3.1-1)
(Ladung eines Elektrons/Protons)
• Allgemein: Ladung q
[q] = 1 C = 1 As, manchmal 1 e = 1 e0
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
3.2 Coulombsches Gesetz
• Zwei elektrische Ladungen q1 und q2
deren Abstand r groß gegenüber ihre
Ausdehnung ist, stoßen/ziehen sich bei
gleichartig/ungleichartiger Ladung mit
der folgenden Kraft ab/an:
q1 ⋅ q2
F =k⋅ 2
r
C. A. Coulomb
(1736 - 1806)
(3.2-1)
mit k =
1
4 ⋅π ⋅ε0
(3.2-2) für das Vakuum
• Influenzkonstante (elektrische Feldkonstante)
ε0 = 8.8542·10-19 A2·s4/(kg·m3)
VAK 5.04.900, WS03/04
(3.2-3)
J.L. Verhey, (CvO Universität Oldenburg )
3.2 Coulombsches Gesetz
• Coulombkraft
vektoriell
r
q1 ⋅ q2 r
F12 = k ⋅ 2 ⋅ e12
r12
q1
+
F21
e12
(3.2-1a)
F12
r12
q2
-
• Gravitationskraft
vektoriell (siehe 1.2.2)
r
m1 ⋅ m2 r
F12 = −G ⋅
⋅ e12
2
r12
(1.2-9a)
m1
F21
e12
F12
m2
r12
• Coulombkraft kann abstoßend • Gravitationskraft ist immer
oder anziehend sein
anziehend
• Ladung bleibt in
• Masse hängt (relativistisch
abgeschlossenen Systemen
betrachtet) vom
immer erhalten
Bewegungszustand ab
Kräfte addieren sich vektoriell (Superpostionsprinzip)
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
3.3 Elektrisches Feldstärke & Flussdichte
• Trägt ein Körper die Ladung q und
erfährt die Kraft F, so ist die elektrische
Feldstärke E am Ort des Körpers
r
r F
E=
q
(3.3-1)
[E] = N/C = kg·m/(A·s3)
Feldstärke einer Punktladung
q1 im Vakuum (3.2-1 & 3.3-1)
r
1 q1 r
E=
⋅ 2 er (3.3-2)
4πε 0 r
VAK 5.04.900, WS03/04
Bemerkung: Ebenso
Gravitationsfeldstärke einer
Masse m1 definierbar
m1 r
r
g = G ⋅ 2 er
r
(3.3-3)
J.L. Verhey, (CvO Universität Oldenburg )
3.3 Elektrisches Feldstärke & Flussdichte
• Anwendung: Millikan-Methode zur Bestimmung der Größe
der Elementarladung
+
+
+
+
+
+
-ze0
mg
-
-
-
-
+
g E
-
-
-
• Öltropchen haben Ladung -z·e0. Das elektrsische Feld des
Kondensator wird in seiner Stärke so eingestellt, dass der
Öltropfen schwebt.
• Masse bestimmbar über Kugelfaserviskosimeter (siehe z.B.
Stroppe, Kap. 15)
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
3.3 Elektrisches Feldstärke & Flussdichte
• (Elektrische) Felder werden durch
Feldlinienbilder dargestellt. Die
Feldlinien zeigen in jenem Punkt in
Richtung der Feldstärke. Die relative
Dichte der Feldlinien ist ein Maß für die
Feldstärke.
Feldlinie
E
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
3.3 Elektrisches Feldstärke & Flussdichte
• Statische elektrische Feldlinien haben ihren
Ursprung und Endpunkt in ruhenden
Ladungen
• Sie gehen immer von positiven zu negativen
Ladungen
• Das statische elektrische Feld ist ein
wirbelfreies Quellenfeld mit Quellen (positive
Ladungen) und Senken (negative Ladungen)
+
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
3.3 Elektrisches Feldstärke & Flussdichte
• Der elektrische Fluss φ ist die Gesamtheit der
Feldlinien, die ein Flächenstück A senkrecht
r r
durchsetzen
φ = ∫∫ EdA
(3.3-4)
[φ] = kg·m3/(A·s3)
• Manchmal auch über den Verschiebungsvektor
(3.3-5)
(im Vakuum) definiert.
D = ε0E
• Für den so definierten elektrischen Fluss Ψ gilt
für eine geschlossene Fläche (z.B Kugel):
r r
Ψ = ∫∫ DdA = ∑ qi
(3.3-6)
[Ψ] = 1 C = 1 A·s
i
(Elektrische Durchflutungsgesetz)
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
3.4 Spannung & Potential
• Entsprechend (1.2-14) ist die im elektrischen
Feld geleistete Verschiebungsarbeit
r r (3.3−1) rr r r
A12 = −∫r Fdr = − q ∫r Edr
r
r2
2
r1
r1
(3.4-1)
• Elektrostatisches Potential:
r r
ϕ (r ) = − ∫ Edr
r
(3.4-2)
∞
+
VAK 5.04.900, WS03/04
Äquipotentialflächen
(ϕ= const.)
J.L. Verhey, (CvO Universität Oldenburg )
3.4 Spannung & Potential
¾ Die elektrische Feldstärke E ist der negative
Gradient des Potentials ϕ
r
r
E = − gradϕ = ∇ϕ
(3.4-3)
• Die Feldlinien zeigen in Richtung des größten
Potentialabfalles.
• Bemerkung: Der Gradient ist (in kartesischen
Koordinaten) wie folgt definiert:
⎛ ∂ϕ ⎞
⎜ ∂x ⎟
r
⎜ ∂ϕ ⎟ ⎛ ∂ϕ r ∂ϕ r ∂ϕ r ⎞
∇ϕ = ⎜
e +
e⎟
=⎜ e +
∂y ⎟ ⎜⎝ ∂x x ∂y y ∂z z ⎟⎠
⎜ ∂ϕ ⎟
⎜
⎟
⎝ ∂z ⎠
VAK 5.04.900, WS03/04
(3.4-4)
J.L. Verhey, (CvO Universität Oldenburg )
3.4 Spannung & Potential
• Spannung zwischen zwei Punkten r1 & r2:
r r
U 12 = − ∫ E d r = ϕ ( r2 ) − ϕ ( r1 )
r2
(3.4-5)
r1
[U]= 1 kg·m2/(A·s3)=1 V (Volt)
• Beispiel: Spannung im Abstand R von einer
Punktladung q gegenüber unendlich
(Potential =0)
(3.4-6)
( 3 .3 − 2 )
r r
U ( R ) = ϕ ( R ) − ϕ (∞ ) = − ∫ E dr + 0 =
( 3 .4 − 5 )
VAK 5.04.900, WS03/04
( 3 .4 − 2 )
R
q
∞
4πε 0 R
J.L. Verhey, (CvO Universität Oldenburg )
3.4 Spannung & Potential
• Kapazität C der freistehenden Kugel/Punkt- Ladung
C = 4πε 0 R
(3.4-7)
• Allgemein C = q/U (3.4-8) [c]=1 F (Farad)=1 C/V
• Kapazität eines Kondensators der Fläche A mit
Abstand d und der Ladung Q:
( 3 .3 − 5 )
( 3 .3 − 6 )
r r E homogen
D
Q
U = − ∫ Edr = E ⋅ d =
⋅d =
⋅d
0
ε0
ε0A
ε0A
⇒C=
(3.4-9)
d
d
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
3.5 Potential an der Zellmembran eines
Neurons
• Ausgangspunkt: Nernstgleichung
• Nernst betrachtete die Diffusion von Elektrolyten unter
Berücksichtigung der Coulombkraft und des
osmotischen Drucks. Daraus konnte er folgenden
Gleichung ableiten (z: Wertigkeit, T: Temperatur, F:
Faradaykonstante 96485,34 C/mol, R Gaskonstante)
R ⋅ T ⎛ [ X ]außen ⎞
E=
ln⎜
⎟
z ⋅ F ⎝ [ X ]innen ⎠
(3.5-1)
• Für einwertig positives Ion bei T=309K(360C) vereinfacht:
⎛ [ X ]außen ⎞
E = 61,3mV ⋅ log⎜
⎟
⎝ [ X ]innen ⎠
VAK 5.04.900, WS03/04
(3.5-2)
J.L. Verhey, (CvO Universität Oldenburg )
3.5 Potential an der Zellmembran eines
Neurons
• Konzentrationsquotient von Kalium plus 1/10
EK = 61,3mV ⋅ log(0,1) = −61,3mV
+
(3.5-3)
• Zellmembran ist dünne isolierende Schicht
wirkt wie Kondensator. Mit Kapazität C = 0,01µF
pro mm2 für die meisten Zellmembranen ist die
Ladung pro mm2 (3.4-8)
( 3.5 −3 )
Q = C ⋅ U = 0,01µF ⋅ 61,3mV = 6,13 ⋅ 10 −10 C
( 3.1−1)
6,13 ⋅ 10 −10 C
9
3
,
8
10
Q =
e
=
⋅
e0
0
-19
1,602176·10 C
VAK 5.04.900, WS03/04
(3.5-3)
(3.5-3a)
J.L. Verhey, (CvO Universität Oldenburg )