1.2.2 Gravitationsgesetz

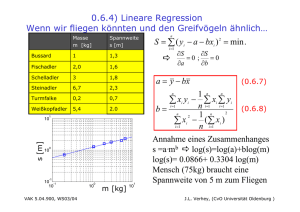
1.2.2 Gravitationsgesetz
•
Herleitung aus Planetenbewegung
•
Keplersche Gesetze
1. Planeten bewegen sich auf Ellipsen
2. Der von Sonne zum Planeten
gezogene Fahrstrahl überstreicht in
gleichen Zeiten gleiche Flächen
3. Die Quadtrate der Umlaufzeit
verhalten sich wie die dritte Potenz
der großen Halbachsen ihrer
Bahnellipsen.
•
Kepler (1571-1630)
Vereinfachung: Annahme einer Kreisbewegung
T2
= const.
3
r
VAK 5.04.900, WS03/04
(1.2-6)
J.L. Verhey, (CvO Universität Oldenburg )
1.2.2 Gravitationsgesetz (Fortsetzung)
• Aus Lex secunda für Kreisbewegung
¾
F = -m·ω2·r
(1.2-7)
(aus 1.2-3 & 1.1-26)
• Mit 1.2.6 und ω=2π/T
¾
F = -m·((2π)2/Τ2) ·r = -const.·m/r2 ·er
(1.2-8)
• Aus Lex tertia
¾ Anziehungskraft F = F(m1, m2)
¾ F~m1 und F~m2
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
1.2.2 Gravitationsgesetz
• Seien m1 und m2 die jeweiligen Massen der
beiden Körper, so ist die Anziehungskraft
gegeben durch
FG =
m1m2G
r2
(1.2-5)
• Gravitationskonstante
G=
6,67·10-11
VAK 5.04.900, WS03/04
Nm2/kg2
(1.2-6)
Zum ersten Mal 1798 von
H.Cavendish (1731 - 1810)
mit Gravitaionswaage
bestimmt
J.L. Verhey, (CvO Universität Oldenburg )
1.2.2 Gravitationsgesetz (Fortsetzung)
• Beispiel: „Gewicht eines Menschen“
• Normalerweise mit Federwaage gemessen
• Auslenkung x proportional zur Kraft F
F=-k·x
(1.2.11)
¾ Kraft und nicht Masse wird gemessen!
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
1.2.2 Gravitationsgesetz (Fortsetzung)
• „Tipp zum Abnehmen“
¾ neuer Wohnort Mond
– mErde =
5,98·1024kg
r=6,378·106m
– mMond = 0,073·1024kg
r=1,738·106m
g=
mG
r2
g Erde =
g Mond
mErdeG
m
=
9
.
809
r2
s2
m G
m
= Mond2 = 1.613 2 = 0.16 g Erde
r
s
VAK 5.04.900, WS03/04
(1.2-12)
(1.2-12a)
(1.2-12b)
Erde
Mond
„75kg“
„12kg“
J.L. Verhey, (CvO Universität Oldenburg )
1.2.2 Gravitationsgesetz (Fortsetzung)
• „Erdlösung zum Abnehmen ungenügend“
• Fallbeschleunigung in Höhe h aus
R2
g ( h) = g
( R + h) 2
g=
mG
(1.2-12)
r2
(1.2-13)
•g = 9.809 kg m/s2 für Höhe R = 6,378 ·106 m
•Höhe h des Mount Everest ca. 9 km
gM. Everest = 0.997·g
„74,8kg“
„75kg“
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
1.2.3 Potentielle Energie
• Arbeit (differentiell) ∆A=F·∆s
• Arbeit
r r
A = ∫ Fds
(1.2-4)
(1.2-5)
• Verschiebungsarbeit
– Wenn Kraft der Bewegung entgegenwirkt, so ist für
Verschiebung ohne Beschleunigung eine entgegengesetzt
gleich große Kraft -F erforderlich
• Beispiel: Arbeit gegen die Schwerkraft
r r
A = −∫ Fds = −m ⋅ g ⋅ h ⋅ cos(π ) = m ⋅ g ⋅ h (1.2-14)
FN
VAK 5.04.900, WS03/04
h
Auf allen Bahnkurven wird
die gleiche Arbeit W=m·g·h
verrichtet!
J.L. Verhey, (CvO Universität Oldenburg )
1.2.3 Potentielle Energie (Fortsetzung)
• Konservative Kräfte
Kräfte, bei denen die gegen sie gerichtete Arbeit
nur von Anfang und Endpunkt der Bewegung
abhängt, d.h. unabhängig vom Weg ist.
• Gespeicherte Arbeit D potentielle Energie
• Energie: Energie kennzeichnet das in einem
System von Teilchen enthaltene
Arbeitsvermögen
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
1.2.3 Potentielle Energie (Fortsetzung)
• Potentielle Energie
(1.2-15)
r r
r r
r
∆EPot = E (r2 ) Pot − E (r1 ) Pot = −∫ Fds ⇒ E (r2 ) = E (r1 ) − ∫ Fds
r
o
o
• Beispiel: Potentielle Energie in Höhe h
Sei E(r1=0) = 0 dann ist (Benutzung von 1.2-14)
E(h)Pot = m ⋅ g ⋅ h
VAK 5.04.900, WS03/04
(1.2-16)
J.L. Verhey, (CvO Universität Oldenburg )
1.2.4 Leistung und kinetische Energie
• Leistung
Die Änderung der Energie pro Zeiteinheit
dE
P=
dt
(1.2.17)
[P] = 1 J/s = 1 W (Watt)
• Kinetische Energie
Mutipliziere (1.2-3) mit dr/dt.
D kinetische Energie
VAK 5.04.900, WS03/04
r r
r& r& d ⎛ 1 r& 2 ⎞
&
&
F ⋅ r = mr ⋅ r = ⎜ m ⋅ r ⎟
dt ⎝ 2
⎠
1 r& 2 1 r 2
Ekin = m ⋅ r = m ⋅ v (1.2-18)
2
2
J.L. Verhey, (CvO Universität Oldenburg )
1.2.5 Mechanischer Energieerhaltungssatz
• In einem konservativen System bleibt die
Gesamtenergie (mechanische Energie)
Eg=Ekin+Epot
(1.2-19)
konstant.
• Gesamtenergie ist Erhaltungsgröße
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
1.2.6 Nichtkonservative Kräfte: Reibung
• Reibungskräfte (Beispiele)
¾ Coulombreibung (trockener Reibung)
FRH=µ0FN
(Haftreibung, 1.2-20)
FRG=µFN
(Gleitreibung, 1.2-21)
¾ Newton Reibung
FRH=1/2·cw·ρ·A·v2
(1.2-22)
Querschnitt des Körpers A, Widerstandskoeffzient cw
Geschwindigkeit v,
VAK 5.04.900, WS03/04
Dichte
ρ = Masse/Volumen
(1.2-23)
J.L. Verhey, (CvO Universität Oldenburg )
1.3 Systeme von Massepunkten
• Impulserhaltung: Wenn keine äußeren
Kräfte anliegen, so bleibt der
Gesamtimpuls erhalten
r
r
r
(1.3-1)
p ges = ∑ pi = ∑ mi ⋅ vi = 0
i
i
• Beispiel Stoß zweier Teilchen
r
r
r
r
m1v1vor + m2 v2 vor = m1v1nach + m2 v2 nach
(1.3-2)
¾ Selbst bei Kenntnis aller Anfangswerte (vor)
noch zwei Unbekannte v1nach & v2nach!
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
1.3 Systeme von Massepunkten
Fortsetzung
(1.3-3)
• Energiebilanz:
1
1
r 2 1
r 2 1
r
r
2
2
m1 (v1vor ) + m2 (v2 vor ) = m1 (v1nach ) + m2 (v2 nach ) + Q
2
2
2
2
Q während des Stosses in innere Energie (z.B.
durch Verformung) umgewandelter Anteil
Q = 0 D elastischer Stoß
• Beispiel: Unelastischer Stoß zweier Teilchen
¾ v1nach = v2nach = vnach
r
r
r
m1v1vor + m2 v2 vor = (m1 + m2 ) ⋅ vnach
(1.3-4)
Q>0
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
1.3 Systeme von Massepunkten
Fortsetzung
• Beispiel: Schiefer elastischer Stoß eines Teilchen
auf ein ruhendes Teilchen mit gleicher Masse
¾ Aus 1.3-2 folgt mit gleicher Masse und v2vor=0
r
r
r
v1vor = v1nach + v2 nach (1.3-5)
¾ Aus 1.3-3 folgt mit gleicher Masse und v2vor=0
sowie Q=0 (elastisch)
v2
v1
nach
r 2
r
r
2
(v1vor ) = (v1nach ) + (v2 nach ) 2
VAK 5.04.900, WS03/04
v1vor
(1.3-6)
nac
h
v1nach senkrecht zu v2nach
J.L. Verhey, (CvO Universität Oldenburg )
1.3.1 Drehbewegungen
• Kinetische Energie eines Massenpunktes bei
gleichförmiger Kreisbewegung
1 r2 1
1 2
2
mv = m ⋅ (ωr ) = Jω
2
2
2
(1.3-7)
mit Massenträgheitsmoment
[J]=1 kg m2
J = mr2
(1.3-8)
• Bei vielen Massepunkten ∆mi gilt entsprechend
J = Σ∆miri2=∫r2dm
(1.3-9)
• Rotationsenergieänderung (nutze 1.1-12d & 1.2-25)
(1.3-10)
dE = F·dr = F·(dφxr) = (rxF)·dφ
M = (rxF)
VAK 5.04.900, WS03/04
(1.3-11) Drehmoment
J.L. Verhey, (CvO Universität Oldenburg )
1.3.1 Drehbewegungen
• Leistung P (nach 1.2-18)
dE d ⎛ 1 2 ⎞
P=
= ⎜ Jω ⎟ = Jω& ω
dt dt ⎝ 2
⎠
(1.3-12)
• Andererseits (nach 1.3-10 mit 1.3-11)
dE
P=
= Mω
dt
(1.3-13)
• Bewegungsgleichung für rotierende Körper
d
M = Jω& = ( Jω ) = L&
dt
(1.3-14)
• mit Drehimpuls
L = Jω
(1.3−15)
Für L gilt entsprechend Drehimpulserhaltungssatz
VAK 5.04.900, WS03/04
J.L. Verhey, (CvO Universität Oldenburg )
Tabelle mit jeweils analogen Größen:
Translation
Rotation
Länge L
Winkel ϕ
Masse m
Trägheitsmoment J (auch Θ)
Geschwindigkeit v
Winkelgeschwindigkeit ω
Impuls p=m⋅v
Drehimpuls L=J⋅ω
Kraft F
Drehmoment M=r×F
Bewegungsgleichung F=dp/dt Bewegungsgleichung
M=dL/dt
(2. Newtonsches Axiom)
kinetische Energie
Ekin=1/2⋅m⋅v2
VAK 5.04.900, WS03/04
Rotationsenergie
Erot=1/2⋅J⋅ω2
J.L. Verhey, (CvO Universität Oldenburg )