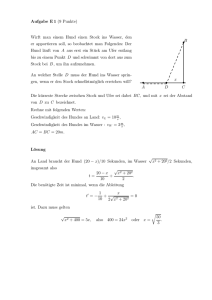
Physik I - ETH Zürich

Physik I
Vorwort
Die Vorlesung ”Physik I”, die ich im SS 07 für die Studenten des Dept. Elektrotechnik/ Informationstechnologie und Materialwissenschaften der ETH
Zürich lese, dient der Einführung in die Mechanik und Elektrodynamik, betrachtet als Grundlagen der klassischen Physik. In dieser Vorlesung wird als
Schwerpunkt berücksichtigt, dass die Physikroutine systematisch Konzepte
der Mathematik benutzt. Das geschieht nicht nur um physikalische Inhalte
korrekt zu vermitteln, sondern trägt auch der Tatsache Rechnung, dass die
Natur selbst eine faszinierende ”mathematische Struktur” besitzt, die in vielen alltäglichen Erscheinungen zum Vorschein kommt. Die für das Studium
der Physik notwendigen Werkzeuge aus der Mathematik werden parallel zu
den physikalischen Konzepten eingeführt. Ich bedanke mich bei meiner Frau
Hedi, die das Skript druck- und webreif bearbeitet hat. Wichtiger Bestandteil
dieser Vorlesung sind die Übungsserien: sie und die Musterlösungen werden
separat aufgeführt. Ich bedanke mich bei N. Saratz (Chef Übungen) und allen
Assistenten für ihren Einsatz.
Zürich, im März 2007,
D. Pescia ([email protected])
http://www.microstructure.ethz.ch
ii
Inhaltsverzeichnis
Vorwort
ii
1 Newtonsche Mechanik
1.1 Newtonsche Bewegungsgleichungen in einer Dimension . . . .
1
2
2 Eindimensionale Mechanik: Beispiele
2.1 Radioaktiver Zerfall . . . . . . . . . . . . . . .
2.2 Kräftefreie Bewegung . . . . . . . . . . . . . .
2.3 K 6= 0 aber konstant . . . . . . . . . . . . . .
2.4 Eindimensionales, homogenes Kraftfeld . . . .
2.5 Der freie harmonische Oszillator . . . . . . . .
2.6 Erzwungene Schwingung . . . . . . . . . . . .
2.7 Gedämpfte Schwingung . . . . . . . . . . . . .
2.8 Resonanzphänomene . . . . . . . . . . . . . .
2.8.1 Elektrische Resonanzkreise . . . . . . .
2.8.2 Spektroskopien . . . . . . . . . . . . .
2.8.3 Resonanzen in der Teilchenphysik . . .
2.9 Allgemeine Lösung 1-dimensionaler Probleme
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 1d Schwingungen mit mehreren Freiheitsgraden
3.1 Eigenmode zweier gekoppelter harmonischer Oszillatoren . . .
3.2 Eigenmode einer schwingenden Kette mit N-gekoppelten Oszillatoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Übergang zum schwingenden Kontinuum: Die Wellengleichung
3.3.1 Die harmonische Welle . . . . . . . . . . . . . . . . . .
3.3.2 Die stehende Welle . . . . . . . . . . . . . . . . . . . .
3.3.3 Eigenfrequenzen eines schwingenden Seils . . . . . . . .
10
10
11
12
13
14
18
22
25
25
26
29
30
33
33
35
37
40
41
41
4 Mechanik im euklidischen Raum
43
4.1 Vektoralgebra . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
4.2 Bewegung eines Massenpunktes im Zentralfeld . . . . . . . . . 47
iii
iv
INHALTSVERZEICHNIS
4.3 Kepler-Problem . . . . . . . . . . . . . . . . . . . . . . . . . . 51
4.4 Rutherfordsche Streuformel . . . . . . . . . . . . . . . . . . . 54
5 Elektrostatik
5.1 Die Grundgleichungen der Elektrostatik . . . . . . . . .
5.2 Das elektrische Feld von einfachen Ladungsverteilungen
5.3 Elektrostatik von Metallen . . . . . . . . . . . . . . . .
5.4 Elektrostatik eines Isolators (= Dielektrikum) . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
58
65
68
75
81
Kapitel 1
Newtonsche Mechanik
Eine der wichtigsten Erscheinungen der Natur ist die Bewegung. Bewegt sich
ein Objekt über Abstände, die viel grösser als seine Ausdehnung sind, so kann
dieses Objekt als Massenpunkt P betrachtet werden. P ist ein geometrischer
Punkt. In der Newtonschen Mechanik ist die Masse m das einzige Merkmal, das Massenpunkte voneinander unterscheidet (Einheiten für die Masse:
kg). Im Falle eines Massenpunktes kann dann seine endliche Ausdehnung für
die Beschreibung der Bewegung vernachlässigt werden. Beispielsweise kann
man für die Beschreibung der Umlaufbahn der Erde um die Sonne die Ausdehnung der Erde vernachlässigen – will man hingegen erklären, warum es
Tag und Nacht gibt, muss man berücksichtigen, dass sich die Erde als Konsequenz ihrer endlichen Ausdehnung um ihre eigene Achse dreht. Die Lage
eines Massenpunktes in einem dreidimensionalen Raum (euklidischer Raum
E3 ) wird als die Linearkombination dreier Basisvektoren gegeben, welche
an einem Punkt (dem Ursprung der Basisvektoren) verankert sind. Die Vektoren wählt man in der Regel orthogonal zueinander: es entsteht ein sog.
kartesisches Koordinatensystem, in welchem der Ortsvektor ~r, der den Ursprung des Koordinatensystems mit dem geometrischen Punkt P verbindet,
durch
~r(t) = x(t)~ex + y(t)~ey + z(t)~ez
dargestellt wird. Die Koeffizienten vor den jeweiligen Basisvektoren sind die
Koordinaten des Punktes entlang der vom Basisvektor spezifizierten Richtung und heissen Komponenten des Vektors ~r. Es sind drei Koordinaten
notwendig, um die Lage eines Massenpunktes zu erfassen: Ein Massenpunkt
P in E3 hat dementsprechend 3 Freiheitsgrade, d.h. seine Lage ist durch
die Angabe von 3 Koordinaten eindeutig festgelegt. Um die Schreibweise
zu vereinfachen, werden vom Vektor ~r nur die Komponenten in Form eines
Zahlentrippels (x(t), y(t)z(t)) beibehalten. In der Mathematik bedeutet das
eine eineindeutige Abbildung von E3 in den Vektorraum der Zahlentrippel.
1
KAPITEL 1. NEWTONSCHE MECHANIK
2
Die Koordinaten sind reelle Zahlen, welche von einem reellen Parameter t
abhängen können. t ist in der Regel die Zeit, und durch die Zeitabhängigkeit
der Koordinaten (die Basisvektoren sind, in diesem spezifischen Fall, zeitunhabhängig) beschreibt der Massenpunkt eine Bahn oder Trajektorie im
Raum. Eine mögliche Einheit für die Zeit ist die Sekunde (sec). Eine mögliche Einheit für die Koordinaten ist das Meter m. Zweck der Newtonschen
Mechanik ist, die Gesetze zur Bestimmung der Bahnkurve anzugeben.
1.1
Newtonsche Bewegungsgleichungen in einer Dimension
Der direkteste Weg, die Bewegung von P zu erfassen, ist die Messung von ~r(t)
über ein gewisses Zeitintervall. Dadurch lässt sich vielleicht ein Gesetz erkennen, mit dessen Hilfe man den weiteren Verlauf der Bewegung voraussagen
kann. So haben Naturwissenschaftler bis und mit Galileo Galilei gearbeitet.
Durch unzählige Beobachtungen hatte man ein sehr genaues Bild, z.B. der
Dynamik der Planeten und der Sterne (fast genau so wie unseres) erlangt,
und konnte damit schon Begriffe wie die jährliche Periodizität der Erdbewegung um die Sonne formulieren. Das Experiment von Galileo auf dem Turm
von Pisa ist in diesem Sinne ein Merkmal in der Geschichte der Physik: Er
lässt eine Kugel aus einer Höhe z0 fallen, misst ihre Lage z als Funktion der
Zeit und schliesst auf ein t2 -Gesetz: z(t) = z0 − 12 gt2 . Galileo war danach im
Stande, die Position der Kugel zu jeder Zeit anzugeben. Allerdings möchte
man die Bewegung durch Gesetze formulieren, die möglichst einfach sind und
es gestatten, eine möglichst grosse Anzahl von Phänomenen zu beschreiben
oder vorherzusagen. Wir werden diesen zweiten, von Newton vorgeschlagenen
Weg, zuerst am Beispiel von eindimensionalen Problemen formulieren.
Eindimensionale Probleme sind dadurch charakterisiert, dass die Bewegung
nur entlang einer Richtung stattfinden kann. Wir wählen die Basisvektoren
so, dass ~ex entlang dieser Richtung liegt. Somit ist die Bewegung des Massenpunktes allein durch die Koordinate x entlang ~ex beschrieben. Die Koordinate
x kann sich als Funktion der Zeit t ändern, d.h. x = x(t) ist eine Funktion
der reellen Variablen t. Mathematisch gesehen, bedeutet das Studium der
Bahn eines Massenpunktes in einer Dimension und die Formulierung seiner
Bewegungsgleichung (BGL) die Untersuchung von reellen Funktionen einer
Variablen.
KAPITEL 1. NEWTONSCHE MECHANIK
3
Reelle Funktionen einer Variablen
Eine reelle Funktion f einer Veränderlichen ist eine Abbildung einer Teilmenge D von
R (Definitionsbereich) nach R: f : x ∈ D → y = f (x) ∈ R. Mit f (x) und g(x) sind
auch das skalare Vielfache c · f (x), die Summe f (x) + g(x) und das Produkt f (x) · g(x)
Funktionen. Mit diesen Operationen können wir aus f (x) = 1 und f (x) = x alle Polynome
P
P∞
P (x) = k ak xk konstruieren. Potenzreihen werden durch k=0 ak xk generiert, falls ein
Intervall für x existiert, innerhalb welchem die Potenzreihe gegen einen endlichenWert
.
konvergiert. Eine weitere wichtige Operation ist der Quotient zweier Funktionen fg (x) =
f (x)
g(x) .
Mit dieser Operation generiert man rationale Funktionen. Der Quotient ist nicht für
Werte von x mit g(x) = 0 definiert. Die Zusammensetzung von Funtkionen, die auch zu
.
einer Funktion führt, ist durch die Gleichung f ◦ g(x) = f (g(x)) definiert. Dabei muss
beachtet werden, dass g(x) im Definitionsbereich von f liegt. Eine wichtige Operation ist
der Grenzwert von Funktionen. Im Definitionsbereich sei eine Zahl c vorgegeben, und eine
Folge von Zahlen an konvergiere nach c, d.h. limn→∞ an = c (die Konvergenz einer Folge
ist gegeben, falls bei jeder vorgegebenen Umgebung ǫ von c alle Zahlen mit k > n innerhalb
ǫ fallen). Wir sagen, für x gegen c strebt f (x) gegen d und schreiben limx→c f (x) = d (lies
Limes x gegen c von f (x) gleich d), wenn für jede gegen c konvergente Folge an aus D stets
die Bildfolge f (an ) gegen d konvergiert. d heisst Grenzwert von f (x) für x → c. Ein für
die Physik wichtiger Spezialfall sind stetige Funktionen. Eine reelle Funktion ist stetig in
x, wenn limy→x f (y) = f (x). Wir erwarten, dass die Bahnkurven von stetigen Funktionen
x(t) beschrieben sind.
Für die Formulierung der Newtonschen BGL ist die Beobachtung wichtig, dass die Trajektorie sowohl von der Lage des Massenpunktes zu einer
vorgegebenen Zeit (die wir als t = 0 wählen können) – der Anfangslage –
abhängt, als auch von seinem Bewegungszustand zur Zeit 0. Ob der Massenpunkt in der Anfangslage still steht oder schon in Bewegung ist, macht
einen grossen Unterschied. Den Bewegungszustand hat Newton mit der Geschwindigkeit des Massenpunktes beschrieben. Die Geschwindigkeit ist die
.
Ableitung der reellen Funktion x(t) nach der Variablen t, d.h. ẋ(t) = dx
. Die
dt
Existenz von einer Schar von Bahnkurven, welche sich aus einem Punkt x(0)
entwickeln können, hat Newton dazu veranlasst, alle möglichen Bahnkurven
als allgemeine Lösung einer Differenzialgleichung für die Beschleunigung
. 2
ẍ(t) = ddt2x zu suchen, woraus die eigentliche Bahn so zu wählen ist, dass die
vorgegebenen Anfangsbedingungen x(t = 0) = x0 , ẋ(t = 0) = v0 erfüllt sind
(2. Newtonsches Axiom):
m · ẍ(t) = K(x, ẋ, t)
Das ist die sogenannte Bewegungsgleichung (BGL). Mathematisch gesehen
handelt es sich um eine (gewöhnliche) Differentialgleichung (DGL) 2. Ordnung. Es gibt dazu eine allgemeine Lösung, die von zwei Integrationskonstan-
KAPITEL 1. NEWTONSCHE MECHANIK
4
ten (Integrationsparametern) abhängt und folglich eine Schar von möglichen
Bahnen beschreibt. Die tatsächliche Bahn, welche die Anfangsbedingungen
erfüllt, ist im Allgemeinen eindeutig bestimmt. Für die Festlegung der Bahn
werden die Integrationskonstanten so gewählt, dass die Anfangsbedingungen
erfüllt sind. Die Grösse an der rechten Seite ist die Kraft (Einheiten: 1N =
1Newton = 1kg sm2 ) und bestimmt, durch die DGL, die eigentliche Dynamik
des Massenpunktes. Die zentrale Frage der Mechanik ist dann, die möglichen
Kräfte zu finden, welche die Bewegung zu jeder Zeit t beeinflussen können.
Falls diese Kräfte bekannt sind, lässt sich die Bahnkurve im Prinzip genau
berechnen, solange wir es schaffen, die BGL zu integrieren. Für die Bestimmung der relevanten Kräfte gibt es leider kein fundamentales Prinzip oder
Protokoll: es ist die Aufgabe der Experimentalphysik genügend Fakten auszuarbeiten, die zu einer Krafthypothese führen können, welche anschliessend
durch weitere Beobachtungen bestätigt oder widerlegt wird.
Differential- und Integralrechung
Die Funktionen, die eine physikalische Bahnkurve beschreiben, müssen eine weitere Eigenschaft besitzen: sie müssen differenzierbar sein.
Definition f heisst im Punkt x0 differenzierbar oder ableitbar, wenn der Grenzwert
limx→x0
f (x) − f (x0 )
x − x0
existiert. Dieser Grenzwert heisst dann Ableitung von f an der Stelle x0 und wird mit
f ′ (x) |x0 oder einfach f ′ (x0 ) bezeichnet. Andere Bezeichnungen für die Ableitung an einer
df
). Die Existenz der Ableitung besagt, dass in der
beliebigen Stelle x sind f˙(x) und dx
Umgebung von x0 , die Werte einer differenzierbaren Funktion durch den Ausdruck
f (x) = f (x0 ) + f ′ (x0 ) · (x − x0 )
sehr gut (exakt im Lim(x−x0 →0 ) approximiert werden können. Diese letzte Formel kann
man auch als
.
f (x) − f (x0 ) = △f ≈ f ′ (x0 ) · △x
schreiben, oder df = f ′ (x) · dx, mit df bekannt als totales Differenzial. Graphisch gesehen:
Lokal kann die Funktion f (x) durch eine Gerade approximiert werden. f ′ (x0 ) ist dann die
Steigung der Tangente am Graph von f (x). Durch diese Definition wird einer Funktion f
eine neue Funktion zugeordnet, und zwar überall dort, wo die Ableitung definiert ist. Die
Differenzierbarkeit einer Funktion an einer Stelle x impliziert die Stetigkeit der Funktion
an dieser Stelle.
Rechenregel:
d
[f (x) + g(x)]
dx
d
[λf (x)]
dx
d
[f (x) · g(x)]
dx
=
f ′ (x) + g ′ (x)
=
λf ′ (x)
=
f ′ (x) · g(x) + f (x) · g ′ (x)(LeibnizP roduktregel)
KAPITEL 1. NEWTONSCHE MECHANIK
5
Abbildung 1.1: Graphische Darstellung zur Berechnung der Ableitung
d f (x)
dx g(x)
=
d
f [g(x)] =
dx
f ′ (x)g(x) − f (x)g ′ (x)
g 2 (x)
f ′ (g(x))g ′ (x)(Kettenregel)
Wir beweisen die (Leibniz) Produktregel und die Kettenregel. Aus f (x) = f (x0 ) +
f ′ (x0 )(x − x0 ) und g(x) = g(x0 ) + g ′ (x0 )(x − x0 ) folgt
f (x) · g(x) = f (x0 )g(x0 ) + [f ′ (x0 )g(x0 ) + f (x0 )g ′ (x0 )](x − x0 )
(Terme in (x − x0 )2 werden vernachlässigt, da sie klein sind) Daraus lässt sich die Produktregel herauslesen. Es gilt weiter
f [g(x)] = f [(g(x0 ) + g ′ (x0 )(x − x0 )] = f (g(x0 )) + f ′ (g(x0 )) · g ′ (x0 )(x − x0 )
woraus die Kettenregel abgelesen werden kann. Eine weitere Regel betrifft die Umkehrfunktion f −1 von f : f −1 (f (x)) = x. Die Umkehrabbildung ist nur dann definiert, wenn f
injektiv ist. Nach der Kettenregel gilt
d −1
f (f (x)) = 1 = (f −1 )′ (f (x)) · f ′ (x)
dx
Mit f(y) =x folgt
(f −1 )′ (x) =
1
f ′ (f −1 (x))
Mit diesen Regeln kann man einige Ableitungen P
konstruieren. Für die Funktionen, die als
Potenzreihe aufgebaut wurden, gilt, aus f (x) = n an xn
X
f ′ (x) =
nan xn−1
n
d.h. man erhält die Ableitung durch ”gliedweise” Differentiation. Man kann auch höhere
Ableitungen definieren, indem f ′ weiter differenziert wird. Somit entsteht f (2) (oder f ′′ ),
die zweite Ableitung von f , wenn man die erste Ableitung f ′ einmal differenziert. Allgemein
KAPITEL 1. NEWTONSCHE MECHANIK
6
n
bezeichnet man auch f (n) als ddxnf die -n-te Ableitung. Die höheren Ableitungen einer
Funktion (falls sie existieren) kann man benutzen um den Entwicklungssatz von Taylor zu
formulieren. Dieser ist sehr wichtig in der Physik, da er erlaubt, physikalische Funktionen
mit Polynomen zu approximieren. Polynome sind ihreseits wichtige Funktionen, die man
relativ leicht manipulieren kann.
Definition. Gegeben sei eine (n+1)-mal differenzierbare Funktion f (x). Das Polynom
Tn =
n
X
f (k) (x0 )
k!
k=0
(x − x0 )k
heisst Taylorpolynom n-ten Grades um den Entwicklungspunkt x0 . Das folgende Theorem
ist als Entwicklungssatz von Taylor bekannt.
Theorem: Zu jedem x gibt es eine Zwischenstelle y zwischen x und x0 so dass
f (x) = Tn (x) +
f (n+1) (y)
(x − x0 )n+1
(n + 1)!
In anderen Worten: Die (n+1)-differenzierbare Funktion f kann um einen Punkt
x0 durch Tn (x) sehr gut approximiert werden, bis auf einen Restterm O[(x −
x0 )]n+1 .
Den Beweis überlassenn wir den Mathematikern. Es stellt sich unmittelbar die Frage, wie
sich das Restglied (die Korrektur) verhält, wenn n wächst, d.h. wie genau kann man f (x)
mit einem Polynom approximieren. Wir betrachten die Folge | f (x) − Tn (x) | im Intervall
[a, b].
f n+1 (y)(x − x0 )n+1
|
(n + 1)!
f n+1 (y)(b − a)n+1
≤ |
|
(n + 1)!
maxf n+1 (b − a)n+1
≤ |
|
(n + 1)!
| f (x) − Tn (x) | = |
f ist beliebig oft differenzierbar und alle Ableitungen sind stetig. Damit existiert ein endlicher Maximalwert von f n+1 (x) für jedes n. Der Ausdruck an der rechten Seite hängt nicht
mehr von x ab. Da die von x unabhängige Folge nach 0 konvergiert für n → ∞ ergibt sich
das Resultat, dass die Approximation von f (x) durch Polynome immer besser wird für
wachsendes n, und zwar für alle x. Welches n reicht, um ein spezifisches Problem korrekt
zu beschreiben, müssen wir von Fall zu Fall entscheiden. Oft wird einfach n = 1 benutzt,
woraus die folgenden nützlichen Näherungsformeln entstehen:
1
1+x
1
1 + x2
ln(1 + x)
sin(x)
cos(x)
√
1+x
exp(x)
≈
1−x
≈
1 − x2
≈
x − x2 /2
≈
≈1+x
1 + x/2
≈
≈
x
1 − x2 /2
7
KAPITEL 1. NEWTONSCHE MECHANIK
mit x ∈ [≈ −0.1, ≈ 0, 1].
Wir betrachten stetige Funktionen, die in einem Intervall J = [a, b] definiert sind
und endlich bleiben. Wir definieren eine endliche Teilmenge Z = a0 = a, a1 , ...., an = b
des Intervalls [a, b] als Zerlegung von J. Zu dieser Zerlegung ordnen wir die Menge
f (a0 ), f (a1 ), ....., f (an ). Damit können wir eine Treppenfunktion T (f ) generieren, die f
stückweise approximiert. Von dieser Treppenfunktion können wir die Summe
n−1
. X
f (ak )(ak+1 − ak )
SZ (f ) =
k=0
konstruieren. SZ (f ) ist, nach Konstruktion, die Fläche, die zwischen T (f ) und der x-Achse
liegt. Dabei rechnen wir Flächeninhalte unter der x-Achse negativ.
Definition: falls der Limes der Riemannschen Summe
limn→∞
n−1
X
k=0
f (ak ) · (ak+1 − ak )
existiert, dann heisst die Funktion f (Riemann)-integrierbar und dieser Limes, den wir
Rb
mit a f (x)dx bezeichen, nennen wir das Integral von f im Intervall [a, b]. Das Integral ist
X
Abbildung 1.2: Graphische Darstellung zur Berechnung des Integrals
dann die Fläche, die unter dem Graphen von f (x) im Intervall a, b liegt. Für die explizite
Berechnung des Limes müssen wir jeweils die Zerlegung feiner machen. Damit reduziert
sich der Abstand zwischen einzelnen Punkten der Zerlegung, aber deren Zahl erhöht sich.
Die damit erzeugte Folge dürfte tatsächlich gegen einen endlichen, berechenbaren Wert
konvergieren.
Wir wollen uns überzeugen, dass integrierbare Funktionen tatsächlich existieren. Wir zerlegen das Intervall [0, 1] mit der Foge a0 = 0, a1 = 1/n, ...ak = k/n, ...n/n = 1 und
R1
versuchen, das ”Integral” 0 x2 dx als Limes der Summe zu berechnen:
n−1
X
k=1
k2 1
·
n2 n
8
KAPITEL 1. NEWTONSCHE MECHANIK
Hier hilft uns die elementare Mathematik, welche solche Summen von Quadraten
tatsächlich berechnen kann: diese Summe beträgt
1
1
1
1
(n − 1) · n · (2n − 1) = −
+
6n3
3 2n 6n2
Der Limes dieser Folge ist 1/3, und das sollte der Flächeninhalt unterhalb des Graphs von
x2 sein. Es lässt sich zeigen, dass jede stetige Funktion tatsächlich integrierbar ist.
Die Definition von Integralen durch Treppenfunktionen ist anschaulich und streng,
sowie es streng ist, den Limes durch explizite Berechnung von konvergierenden Folgen zu
suchen. Die tatsächliche Berechnung von Integralen erfolgt aber durch den Hauptsatz der
Differenzial- und Integralrechnung.
Theorem. Gegeben sei eine stetige Funktion im Intervall [a, b] und x0 , x seien beliebige
Werte im Intervall. Dann ist
Z x
f (x)dx = F (x) − F (x0 )
(i)
x0
(ii)F ′ (x)
= f (x)
Die Funktion F (x) welche (i) erfüllt, heisst Stammfunktion von f (x). Die Stammfunktion hat die wichtige Eigenschaft, dass ihre Ableitung am Punkt x im Intervall [a, b] mit
f(x) übereinstimmt. Hat man eine Stammfunktion konstruiert, so ergeben sich alle anderen
durch Addition einer beliebigen Konstanten.
Von diesem Theorem geben wir eine Plausibilitätsbetrachtung. Wir betrachten den Summand f (ak )(ak+1 − ak ) für sehr kleine Intervalle ak+1 − ak und schreiben, im Sinne der
Taylor Approximation
.
f (ak )(ak+1 − ak ) = F (ak+1 ) − F (ak )
Im Sinne des Taylor Entwicklungssatzes ist F (ak ) leicht zu identifizieren als die Funktion,
für welche F ′ (x) |ak = f (x) |ak . Somit ergibt sich (ii). In der Summe über k von den
Gliedern F (xk+1 ) − F (xk ), startend von ak=0 = x0 bis ak=n = x, fallen alle Terme in
der Summe aus, ausser F (a0 ) und F (an ), die nicht kompensiert werden.
R Somit ergibt sich
die Behauptung (i). Die Stammfunktion von f (x) wird formell als f (x)dx bezeichnet.
Integrale ohne Integrationsgrenzen bezeichnen also Integrale oder Stammfunktionen. Aus
diesem Satz ergeben sich auch einige wichtige Rechenregeln.
1.
Z c
Z b
Z c
f (x)dx
f (x)dx =
f (x)dx +
a
b
a
2.
Z
a
b
f (x)dx = −
Z
a
f (x)dx
b
3.
Z
a
b
[f1 (x) + f2 (x)]dx =
Z
a
b
f1 (x)dx +
Z
a
b
f2 (x)dx
9
KAPITEL 1. NEWTONSCHE MECHANIK
4.
Z
a
b
λ · f (x)dx = λ
Z
b
f (x)dx
a
5.
d
dx
Z
x
f (t)dt = f (x)
a
Substitutionsregel. Die Umkehrung der Kettenregel ergibt die folgende Integrationsformel, die durch Ableiten der rechten Seiten bewiesen werden kann. Gegeben f : [a, b] →
[c, d], stetig und differenzierbar und g : [c, d] → R stetig mit Stammfunktion G(x). Dann
Z
g(f (x))f ′ (x)dx = G(f (x))
Für das bestimmte Integral bedeutet dies,
Z
a
b
g(f (x)f ′ (x))dx = G(f (b)) − G(f (a)) =
Z
f (b)
g(t)dt
f (a)
Die Integrationsgrenzen müssen mitransformiert werden.
Partielle Integration. Für stetig differenzierbare Funktionen f und g gilt
Z
Z
f (x) · g ′ (x)dx = f · g − f ′ (x)g(x)dx
Grund: Nach der Produktregel ist f g ′ + g ′ f = (f g)′ , und die Stammfunktion von (f g)′ ist
f g. Für das bestimmte Integral bedeutet dies
Z
a
b
f (x)g ′ (x)dx = f g |ba −
Z
a
b
f (x)g ′ (x)dx
Kapitel 2
Eindimensionale Mechanik:
Beispiele
2.1
Radioaktiver Zerfall
Die BGL sind gewöhnliche Differentialgleichungen (DGL). Damit ist eine
Verknüpfung gemeint, die nicht nur die gesuchte Bahn enthält, sondern
auch deren erste und zweite Ableitung. Zum Einstieg in die Welt der DGL
betrachten wir den radioaktiven Zerfall. Das ist kein mechanischer Vorgang,
aber ist durch eine sehr bekannte und wichtige DG beschrieben, nämlich
y ′ = −y/λ, mit y = y(s). λ ist eine feste, charakteristische Zeit, s ist
die Variable. Diese DGL besagt, dass die y ′ – die zeitliche Änderung der
Funktion y – proportional zu y ist. Je mehr ”Atome” der radioaktiven Sorte
y wir haben, desto grösser ist die Menge, welche radioaktiv zerfällt. Wir
wollen die Lösung zur Anfangsbedingung y(t0) = y0 finden.
Diese DGL ist vom Typ ” DGL mit getrennten Variablen”, d.h. y ′ = f (s, y) = g(s) ·
h(y). Solche DGL können wir folgenderweise integrieren:
y ′ (s)
= g(s)
h(y(s))
Integrieren beider Seiten von t0 bis t ergibt
Z t ′
Z y(t)
Z y
Z t
y (s)
1
du
g(s)ds
ds =
=
du =
t0 h(y(s))
y(t0 ) h(u)
y0 h(u)
t0
Dies ergibt eine implizite Bestimmungsgleichung für y(t), die nur eine Integration und
Anfangsbedingungen involviert.
In unserem Spezialfall ergibt dieses Verfahren
Z
y
y0
Z t
−1
1
du =
du
u
t0 λ
10
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
11
bei welchem die Lösung
y(t) = y0 · e−
(t−t0 )
λ
ist. Dies ist die Lösung der ursprünglichen DGL, welche auch die Anfangsbedingungen erfüllt.
Zur Berechnung der allgemeinen Lösung kann man formell auch folgenderweise vorgehen. Aus
dy
= h(y) · g(s)
ds
schreibt man
dy
= g(s) · ds
h(y)
Durch
Integration beider Seiten findet man eine
Stammfunktion H(y) =
R dy
R
und
alle
Stammfunktionen
G(s,
A)
=
g(s)ds,
die durch eine frei
h(y)
wählbare Konstante A parametrisiert sind. Schafft man es, die Gleichung
H(y) = G(s, A) nach y aufzulösen, so findet man die allgemeine Lösung
y(s, A) mit A der Integrationskonstanten.
Interessante Anwendungen hat diese DGL und deren Lösung für die Altersbestimmung organischer Objekte. Zur Zeit des Todes (t0 ) hören organische
Substanzen auf, C 12 – die stabile Version von Kohlenstoff – und das radioaktive Isotop C 14 aufzunehmen. Bis t0 sind beide Formen von C mit einer
N 14 (t0 )
bekannten relativen Konzentration NC12
– die wir aus heutigen MessunC (t0 )
gen kennen – vorhanden. Misst man deren relative Konzentration zu einer
späteren Zeit t (etwa die Gegenwart), dann erwarten wir
NC 14 (t0 ) − t−t0
NC 14 (t)
=
·e λ
NC 12 (t)
NC 12 (t0 )
Bei bekannter Halbwertszeit λ des radioaktiven Isotops C14 lässt sich aus
der Messung der relativen Konzentration der beiden Arten Kohlenstoff t − t0
sehr genau festlegen (die Genauigkeit hängt davon ab, wie genau wir die
Konzentration messen können).
2.2
Kräftefreie Bewegung
Die einfachste Kraft ist K ≡ 0: die obige Gleichung besagt, dass die zweite Ableitung der Bahnkurve nach der Zeit 0 ist. Somit ist die allgemeinste
Lösung der Newtonschen BGL ẍ = 0
x(t) = A + B · t
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
12
(verifizieren Sie das Resultat durch explizites zweimaliges Ableiten nach t des
obigen Ausdrucks). A und B sind Integrationskonstanten, welche so festgelegt
werden müssen, dass die Anfangsbedingungen x(t0 ) = x0 und ẋ(t0 ) = v0
erfüllt sind. Dies ergibt ein Gleichungssystem für A und B
x0 = A + B · t0
v0 = B
mit Lösung B = v0 und A = x0 − v0 · t0 . In Worten: Ohne Kraft bewegt sich
ein Massenpunkt entlang einer Geraden mit konstantem Geschwindigkeit (1.
Newtonsches Axiom).
2.3
K 6= 0 aber konstant
Die BGL lautet
ẍ =
K
m
Integration auf beiden Seiten ergibt
ẋ =
K
·t+A
m
Erneute Integration ergibt
x(t) =
K
· t2 + A · t + B
2·m
mit den beiden Integrationskonstanten A, B. Diese Gleichung stellt die allgemeine Lösung dar. Die Anfangsbedingungen seien x(t0 ) = x0 und ẋ(t0 ) = v0 .
Die Bahn zu diesen Anfangsbedingungen finden wir durch die Lösung des
Gleichungssystems für A, B:
K
· t2 + A · t0 + B
2·m 0
K
· t0 + A
=
m
x0 =
v0
Dies ergibt
A = v0 −
K
· t0
m
B = x0 − (v0 −
K
K
· t0 ) · t0 −
· t2
m
2·m 0
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
13
Somit ist die gesuchte Bahn zu den vorgegebenen Anfangsbedingungen
x(t) =
K
(t − t0 )2 + v0 (t − t0 ) + x0
2m
Als Anwendung dieser Formel betrachten wir K = −mg (Galileo Experiment). Aus v0 = 0 ergibt sich das Galileo Gesetz
| x(t) − x0 |=
g 2
·t
2
In Worten: Ohne Reibung und Luftwiderstand braucht eine Masse,qdie sich
auf einer Höhe x0 oberhalb der Erdoberfläche befindet, eine Zeit 2 xg0 um
den Boden zu erreichen.
2.4
Eindimensionales, homogenes Kraftfeld
Wir betrachten ein Kraftfeld
Kx (x, y, z) = 0
Ky (x, y, z) = 0
Kz (x, y, z) = −m · g
welches im Euklidischen Raum definiert ist und uniform ”nach unten” zeigt.
x, y, z sind Kartesische Koordinaten. In diesen Koordinaten gilt das Trennungspostulat von Newton:
mẍ = Kx (x, y, z) = 0
mÿ = Ky (x, y, z) = 0
mz̈ = Kz (x, y, z) = −m · g
Das bedeutet: die Beschleinigungen sind in den jeweiligen kartesischen Koordinaten nur von den entsprechenden Komponenten des Kraftvektors beeinflusst. In unserem Fall lautet die allgemeine Lösung:
x(t) = Ax t + Bx
y(t) = Ay t + By
−g 2
t + Az · t + Bz
z(t) =
2
mit den 6 Integrationskonstanten Ax , Bx , Ay , By , Az , Bz . Für einen Wurf aus
einer Höhe z0 haben wir die Anfangsbedingugen
x(t = 0) = y(t = 0) = 0
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
14
ẏ(t = 0) = ż(t = 0) = 0
z(t = 0) = z0
ẋ(t = 0) = v0
ż(t = 0) = 0
Das dazugehörige Gleichungssystem für die Integrationskonstante ergibt die
Lösung
Ay
Bz
Az
Ax
=
=
=
=
By = Bx = 0
z0
0
v0
Somit ergibt sich die Bahn
x(t) = v0 · t
y(t) ≡ 0
−g 2
t + z0
z(t) =
2
Aus der ersten Gleichung folgt t =
x(t)
.
v0
z(x) =
Eingesetzt in der dritten ergibt
−g 2
x + z0
2v02
Mathematisch gesehen ist dies die Gleichung einer nach unten geöffneten
Parabel mit Ursprung (0, 0, z0 ). Je grösser die Anfangsgeschwindigkeit v0 ist,
desto kleiner ist die Krümmung der Parabel, desto weiter fliegt die Masse
entlang der x-Koordinate, bevor sie den Boden erreicht.
2.5
Der freie harmonische Oszillator
Es stellt sich heraus, dass sich K(x) oft als das Negative der Ableitung nach
x einer sogenannten potentiellen Energie darstellen lässt: K(x) = − dUdx(x) .
U(x) wird als die potentielle Energie der Bewegung bezeichnet. Die Abbildung gibt den Verlauf der potentiellen Energie, welche zum Beispiel bei der
chemischen Bindung zweier Atome aus der Quantenmechanik erwartet wird.
Die Atome sind entlang einer Geraden angeordnet, die Koordinate x bezeichnet deren Abstand. Einen zur Abbildung ähnlichen Verlauf beobachtet man
für das Paarpotential bei der chemischen Bindung aller Arten. Die potentielle
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
15
Abbildung 2.1: Graphische Darstellung von U(x)
Energie ist durch ein Minimum x0 von U(x) charakterisiert, welches einen
Gleichgewichtsabstand zwischen den Atomen darstellt. Die Bindungsenergie
beträgt U(x0 ). Das bedeutet, dass das Angehen einer Bindung zu einer Energiesenkung gegenüber freien Bestandteile führt. Warum bei x0 zwei Atome
”gebunden” sind, kann auch ”mechanisch” erklärt werden: sollte ein Atom
versuchen, die Gleichgewichtslage zu verlassen, spürt es eine rücktreibende
, die es wieder zu x0 führt. Bei x0 selbst ist die auf die Bestandteile
Kraft − dU
dx
wirkende Kraft genau Null: das Molekül ist im Grundzustand und, mechanisch gesehen, sind die Atome in Ruhe. Angeregte Zustände kann man erreichen, indem man (zum Beispiel durch Einstrahlung von Licht oder Wärmezufuhr) den Abstand der beiden Atome leicht verkleinert oder vergrössert.
Daraus entsteht eine Bewegung, welche als Schwingung bekannt ist. Schwingungen sind wichtige angeregte Zustände von Molekülen und Festkörpern.
Schwingungen sind ein sehr verbreiteter Bewegungstyp mechanischer Systeme. Atome in Molekülen und Festkörpern können zum Schwingen gebracht
werden, und die spektroskopische Untersuchung solcher Schwingungzustände
ist ausserordentlich nützlich, sowohl in der Physik als auch in der Chemie und
Biologie.
Die BGL für die Bewegung in einem solchen Kraftfeld ist
mẍ(t) = −
dU(x)
dx
In der Nähe des Minimums lässt sich U(x) folgendermassen approximieren:
U(x) ≈ U(x0 ) + (x − x0 ) · U ′ (x0 ) +
(x − x0 )2 ′′
U (x0 )
2!
Da U(x) bei x0 ein Minimum besitzt, ist U ′ (x0 ) = 0. Das erste nicht ver-
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
16
schwindende Glied ist das proportional zu (x − x0 )2 . Damit ist
U(x) = U(x0 ) + (x − x0 )2
U ′′ (x0 )
2
Diese Näherung, die nur für kleine Schwingungen gilt, heisst harmonische
Approximation. In der harmonischen Näherung, lässt sich die BGL als
mẍ = −U ′′ (x0 ) · (x − x0 )
′′
.
schreiben. Üblicherweise setzt man die Grösse U ′′ (x0 ) = k und U m(x0 ) =
ω02 (Einheit: s12 ). Die Bedeutung von ω0 als charakteristische Frequenz der
Bewegung wird bald klar. Somit ist die BGL (für die Variable u = x − x0 ),
die die Abweichung von der Gleichgewichtskoordinate x0 beschreibt
ü + ω02 u = 0
Diese DGl gehört zur Klasse der linearen DGL nter-Ordnung mit konstanten Koeffizienten:
an y (n) + an−1 y (n−1) + ... + a1 y ′ + a0 y = g(x)
Falls die ”Störfunktion” g(x) verschwindet, ist die DGL homogen. Die Lösung der homogenen DGL suchen wir durch den Ansatz y(t) = eλt . Das führt zu einer algebraischen
Gleichung für λ:
an λn + an−1 λn−1 + ... + a1 λ + a0 = 0
Die Nullstellen λi können komplex sein. Jede Nullstelle λi generiert eine Exponentialfunktion eλi ·t , welche die DGL löst. Falls alle Nullstellen verschieden sind, dann haben
wir n linear unabhängige Lösungen für die DGL n-ter Ordnung gefunden. Sie bilden ein
Fundamentalsystem von Lösungen: jede andere Lösung lässt sich als Linearkombination
P
λi ·t
. Sollte g(x) 6= 0 sein, dann ist die
der Grundlösungen darstellen: yhom (t) =
i αi e
DGl inhomogen. Die allgemeine Lösung der inhomogenen DGL ist die Superposition einer
speziellen Lösung der inhom. DGL mit der allgemeinen Lösung der hom. DGL.
Die zum freien harmonischen Oszillator gehörige charakteristische (algebraische) Gleichung ist λ2 + ω02 = 0, mit der allgemeinen Lösung u(t) =
C1 cos(ω0 t) + C2 sin(ω0 t) = A · cos(ω0 t + ϕ), mit
1. ω0 : Eigen(kreis)frequenz
2. A: maximale Amplitude
3. ϕ: Phasenwinkel
ω0 : Eigenfrequenz
4. ν = 2π
5. T =
1
ν
=
2π
:
ω0
Schwingungsdauer (Periode)
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
17
Einige Spezialfälle verdienen besondere Beachtung.
1. Wir lenken den Oszillator anfangs um u0 aus, lassen ihn dann los und
betrachten seine Schwingung. Die Anfangsbedingungen lauten offenbar
u(0) = u0 , u̇(0) = 0. Die Lösung zu diesen Anfangsbedingungen ist
deshalb u(t) = u0 cos ω0 t. Die Anfangselongation ist gleichzeitig die
maximale Amplitude der Schwingung.
2. Wir stossen den Körper in seiner Ruhelage an und verleihen ihm die
Geschwindigkeit v0 , u(0) = 0, v(0) = v0 . Dies führt zu u(t) = ωv00 sin ω0 t.
Die maximale Amplitude der Schwingung ist somit A = ωv00 .
Ein wichtiges Merkmal der Schwingung in der harmonischen Näherung ist die
Unabhängigkeit von T von der Amplitude A, wie die explizite Lösung zeigt.
Darüberhinaus erkennen wir eine weitere Grösse, die während der ganzen
Bewegung den gleichen Wert annimt: es ist die totale Energie des Massenpunktes, die sich aus der kinetischen Energie 21 mu̇2 und der potentiellen
Energie 12 ku2 zusammensetzt (wir wählen U(x0 )=0). Es gilt nämlich
1
mA2 ω02 sin2 (ω0 t + ϕ)
2
m 2 2
1
mω02 A2 cos2 (ω0 t + ϕ) =
· ω0 · A
+
2
2
Ekin + U(u) =
Die totale Energie ist eine Erhaltungsgrösse der Bewegung.
Bemerkungen.
• Wir haben bereits bemerkt, dass die Kraft K(x) als Negative der Ableitung nach der Ortskoordinate einer potentiellen Energie abgeleitet
pot (x)
werden kann: K(x) = −dUdx
. Bei vorgegebenem K(x) lässt sich eine
potentielle Energie definieren, als
Upot (x) = −
Z
K(x)dx
wobei diese Definition klar macht, dass die potentielle Energie nur bis
auf eine additive Konstante definiert ist. Die Einheit der potentielle
.
Energien sowie der totalen Energie ist N · m = Joule (gekürzt J).
• Die Arbeit einer Kraft auf dem Weg zwischen den Ortskoordinaten x1
und x2 ist als
Z
. x2
A(x1 → x2 ) =
K(x)dx
x1
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
18
definiert. Schreiben wir dx als ẋ(t)dt, lässt sich die Arbeit als ein Integral über die Zeit schreiben:
.
A(t1 → t2 ) =
Z
t2
t1
K(x(t))ẋdt
.
mit x(ti ) = xi . Der Integrand K(x) · ẋ hat die Einheiten J/sec =
W att (gekürzt W ) und wird Leistung der Kraft zur Zeit t genannt. Die
Bedeutung der Arbeit ist aus folgender Überlegung klar.
A(x1 → x2 ) = Upot (x1 ) − Upot (x2 )
Etot (x2 ) − Etot (x1 ) = (Upot (x2 ) − Upot (x1 )) + (Ekin (x2 ) − Ekin (x2 ))
= ∆Ekin + ∆Epot
= ∆Ekin − A(x1 → x2 )
Falls die totale Energie erhalten bleibt, ist
A(x1 → x2 ) = ∆Ekin
In Worten: die Kraft leistet Arbeit, um die kinetische Energie zu ändern.
2.6
Erzwungene Schwingung
Wir gehen nun zur Betrachtung von Schwingungen eines Systems über, auf
das ein äusseres veränderliches Feld wirkt. Derartige Schwingungen heissen
erzwungene Schwingungen im Gegensatz zu den im vorherigen Paragraphen
untersuchten freien Schwingungen. Bei der Anwesenheit eines äusseren Feldes
besitzt das System neben der eigenen potentiellen Energie 1/2k(x − x0 )2
ausserdem die potentielle Energie V (x, t), die von der Wirkung des äusseren
Feldes herrührt. Wenn wir dieses Zusatzglied in einer Potenzreihe der kleinen
Grösse x entwickeln, erhalten wir
V (x, t) = V (x0 , t) + (x − x0 )
∂V ∂x x=x0
Das erste Glied hängt nur von der Zeit ab und
kommt bei der Aufstellung
∂U der BG nicht vor. Im zweiten Glied ist − ∂x die äussere Kraft, die auf
x=x0
das System in der Gleichgewichtslage wirkt und eine vorgegebene Funktion
der Zeit ist. Wir bezeichnen sie mit F (t). Die BGL lautet
ü + ω02 · u =
1
F (t)
m
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
19
wo wir wiederum die Frequenz ω0 der freien Schwingung eingeführt haben.
Wir betrachten nun einen Fall von besonderem Interesse, bei dem die äussere
Kraft ebenfalls eine einfache periodische Funktion der Zeit mit der Frequenz
γ ist: F (t) = f · cos γt darstellt. Um eine spezielle Lösung zu suchen, führen
wir den Ansatz usp = b cos γt durch, mit dem gleichen periodischen Faktor.
Einsetzen in die DG ergibt die charakteristische Gleichung
f
=0
m
bγ 2 − bω02 +
deren Lösung b =
f
m(ω02 −γ 2 )
ist. Die allgemeine Lösung der inhom. DG ist
A cos(ω0 t + ϕ) +
f
cos γt
− γ2)
m(ω02
Die freien Konstanten A und ϕ bestimmen sich aus den Anfangsbedingungen. Das bedeutet, dass das System unter der Wirkung äusserer periodischer
Kräfte eine Bewegung ausführt, die sich aus zwei Schwingungen zusammensetzt. Aus einer Schwingung mit der Eigenfrequenz ω0 des Systems und aus
einer Schwingung mit der Frequenz γ der äusseren Kraft. Der Verlauf der
Amplitude der speziellen Lösung ist in der folgenden Skizze dargestellt: Die
negative Amplitude für γ ≥ ω0 kann man auch als positive Amplitude einer
um −π verschobenen cos γt darstellen, d.h. die Lösung lässt sich als
A cos(ω0 t + ϕ) + |
A cos(ω0 t + ϕ) + |
darstellen.
f
| cos γt, γ < ω0
− γ 2)
m(ω02
f
| cos(γt − π), γ > ω0
− γ 2)
m(ω02
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
20
Die gegebene Lösung gilt nicht im Fall der sog. Resonanz, d.h. wenn
die Frequenz der äusseren Kraft mit der Eigenfrequenz des Systems zusammenfällt. Um die allgemeine Lösung der BG in diesem Falle zu finden, versuchen wir eine spezielle Lösung mit dem Ansatz
usp = b(cos γt − cos ω0 t)
zu finden. Die Motivation für diesen Ansatz ist die Folgende: In der vorigen
Lösung strebte der Nenner für γ → ω0 nach Null. Damit diese Divergenz auf
irgendeine Weise kompensiert wird und eine wohldefinierte Lösung existiert,
müssen wir dafür sorgen, dass auch der Zähler für γ → ω0 nach 0 strebt.
Einsetzen in der DG (zuerst nehmen wir formell γ 6= ω0 ) ergibt
−bγ 2 cos γt + bω02 cos ω0 t + bω02 (cos γt − cos ω0 t)
= b(ω02 − γ 2 ) cos γt
f
=
cos γt ⇒
m
f
b =
2
m(ω0 − γ 2 )
Die Funktion, die die Lösung im Fall der Resonanz darstellt, finden wir als
Resultat von
f
γ=ω +ε
lim [
(cos γt − cos ω0 t)] =0
γ→ω0 m(ω 2 − γ 2 )
0
= lim[
ε→0
f
cos((ω0 + ε)t) − cos ω0 t]
m(2ω0 + ε)(−ε)
Durch Benutzung der triginometrischen Identität cos(α + β) = cos α cos β −
sin α sin β erhalten wir
cos((ω0 + ε)t) − cos ω0 t = cos ω0 t · cos εt − sin ω0 t · sin εt − cos ω0 t
kleines ε
=
cos ω0 t · 1 − sin(ω0 t) · εt − cos ω0 t
und
lim[
ε→0
f
cos(ω0 + ε)t − cos ω0 t]
m(2ω0 + ε)(−ε)
=
=
f
εt · sin ω0 t
2mω0 ε
f
t
2mω0
· sin ω0 t
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
21
Die allgemeine Lösung lautet dann
f
t · sin ω0 t
2mω0
u(t) = A · cos(ω0 t + ϕ) +
Im Resonanzfall, steigt die Schwingungsamplitude linear mit der Zeit (solange sie nicht so gross wird, dass die gesamte dargelegte Theorie nicht mehr
anwendbar ist!). Die Erscheinung der Resonanz hat viele Anwendungen in
Abbildung 2.2: Verlauf der Schwingung im Resonanzfall
der Physik und überhaupt in den Naturwissenschaften. Auf einige davon
werden wir näher eingehen. Die Resonanz kann aber auch sehr gefährlich
werden, z.B. für Maschinenteile wie Turbinenwellen, wenn die Eigenfrequenz
der Welle gleich ihrer Umlauffrequenz wird. Beim Anfahren von Gasturbinen, bei denen die Betriebsfrequenz oberhalb der Eigenfrequenz liegt, muss
deshalb möglichst schnell über die Resonanzstelle hinweg gefahren werden.
Neben der Amplitude ist auch die von der äusseren Kraft zugeführte Energie eine Grösse, die oft den Resonanzprozess charakterisiert. Nach unseren
Definitionen ist die in einer Periode τ = 2π/ω0 zugeführten Arbeit
ւ
A
=
Z
u(t)
u(0)
ւ
F dx =
Z
τ
0
F ւ (t)
du
dt
dt
Wir unterscheiden zwischen zwei Fällen: γ 6= ω0 und γ = ω0 . Im ersten Fall ist
die zugefügte Energie (oder, anders ausgedrückt, die vom System absorbierte
Energie) null:
−
Z
τ
0
f · cosγt
f
γ · sinγt ∝
2
m(ω0 − γ 2 )
Z
0
τ
cosγt · sinγt =
t
= cosγt · sinγt = 0 !
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
22
Nur im Resonanzfall ist das System imstande, Energie zu absorbieren,
nämlich
Z
0
τ
f2
f2 Z τ
t · cos2 ω0 t dt =
ω0 · cosω0 t · t · cosω0 t dt =
2mω0
2m 0
f2 2
f2 τ2 τ2
( − )=
τ
2m 2
4
8m
Diese Möglichkeit, nur bei der Resonanz einem System Energie zuzuführen,
ist die Grundlage für die Absorption von Licht durch Materie, und findet zum
Beispiel in der Spektroskopie eine wichtige Anwendung (die τ 2 -Abhängigkeit
=
der absorbierten Energie wird in der Tat nicht beobachtet: Man beobachtet eher eine τ Abhängigkeit, die dazu führt, dass die absorbierte Energie pro Zeiteinheit konstant ist.
Wir werden sehen, wie die Einführung der Dämpfung zur nötigen Korrektur führt.)
2.7
Gedämpfte Schwingung
Bis jetzt haben wir angenommen, dass die Bewegung der Masse im leeren
Raum stattfindet, oder dass der Einfluss des Mediums auf die Bewegung
vernachlässigbar ist. In Wirklichkeit setzt das Medium der Bewegung des
Körpers einen Widerstand entgegen, der sie zu verlangsamen sucht (Reibung). Die Reibung modifiziert den Ablauf der Bewegung, wie wir im konkreten Fall des harmonischen Oszillators berechnen wollen. Man simuliert
oft Reibung, indem man eine Reibungskraft in die BGL einführt. Eine solche Reibungskraft nimmt für den hier betrachteten Fall der eindimensionalen Schwingung die Form fD = −D · ẋ, D > 0 an. Das Minuszeichen
bedeutet, dass die Kraft der Bewegung entgegenwirkt. Wenn wir diese Kraft
auf der rechten Seite der BG hinzufügen, erhalten wir (zuerst sei F = 0)
k
= ω02 ,
mü = −ku − D u̇. Wir teilen durch m und führen die Bezeichnungen m
D
= 2λ ein. Dabei ist ω0 die Frequenz der freien Schwingungen des Systems
m
ohne Reibung. Die Grösse 2λ heisst Dämpfungskonstante. Auf diese Weise
erhalten wir die Gleichung
ü + 2λu̇ + ω02 u = 0
Nach den allgemeinen Regeln für die Lösung linearer DG mit konstanten
Koeffizienten setzen wir den Ansatz x = er·t und finden die charakteristische
q
Gleichung r 2 + 2λr + ω02 = 0 mit den Lösungen r1,2 = −λ ± λ2 − ω02 . Die
allgemeine Lösung der Gleichung ist
u(t) = c1 er1 t + c2 er2 t
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
23
Hier müssen zwei Fälle unterschieden werden: Für λ < ω0 erhalten wir zwei
komplex konjugierte Werte für r1,2 :
q
r1,2 = −λ ± i |λ2 − ω02 |
Die allgemeine Lösung der DG ist
u(t) = Ae−λt cos(ωD · t + ϕ)
. q
ωD = |λ2 − ω02 |. Die durch diese Formel dargestellte Bewegung ist eine
sog. gedämpfte Schwingung. Man kann sie als harmonische Schwingung mit
exponentiell abnehmender Amplitude ansehen. Die Schwingungsfrequenz ist
kleiner als die Frequenz der freien Schwingung ohne Reibung. Wir nehmen
jetzt an, dass λ > ω0 ist. Dann sind beide Werte von r reell und negativ. Die
allgemeine Lösung lautet hier
√ 2 2
√ 2 2
u(t) = c1 e−(λ− λ −ω0 )t + c2 e−(λ+ λ −ω0 )t
Die Bewegung besteht aus einer asymptotischen (bei t → ∞) Annäherung an
die Gleichgewichtslage ohne Schwingung. Diese Bewegung heisst aperiodisch.
Im Automobilbau ist das die Aufgabe der Stossdämpfer, die durch starke
Bodenunebenheiten entstehenden unangenehmen und auch gefährlichen Federschwingungen der Karrosserie sofern als möglich aperiodisch zu dämpfen.
In beiden Fälle wird eine allfällige Anfangsabweichung aus der Ruhelage mit
der Zeit abnehmen, bis die Masse wieder in die Ruhelage zurück ist. Dämpfung spielt natürlich auch bei erzwungenen Schwingungen eine grosse Rolle.
Sie modifiziert den Verlauf des Resonanzvorganges, indem sie auch entfernt
von der Resonanz zur Arbeitsübertragung zwischen äüssere Kraft und System führt. Dabei bremst sie das Wachstum der Amplitude im Resonanzfall
zu einem endlichen, stationären Wert. Die DG lautet
ü + 2λu̇ + ω02 u =
f
cos γt
m
Die allgemeine Lösung ist dann (ohne Herleitung)
u(t) = A · e−λt cos(ωD t + ϕ) + b · cos(γt + δ)
mit b =
√
m
f
(ω02 −γ 2 )+4λ2 γ 2
und tan δ =
2λγ
.
γ 2 −ω02
Der erste Summand nimmt mit
der Zeit exponentiell ab, sodass nach genügend langer Zeit nur noch der
”erzwungene” Term b · cos(γt + δ) übrig bleibt (aus diesem Grund eignen sich
Experimente zur Visualisierung der speziellen Lösung!!) Die Phase wechselt
24
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
0
0
0
0
Abbildung 2.3: Die Phase δ und die Amplitude b als Funktion von γ für zwei
verschiedene Parameter λ
nicht sprunghaft von 0 zu −π wie beim Fall λ = 0. Der Wechsel findet in
einem engen Frequenzbereich der Breite 2λ in der Umgebung von ω0 statt.
Am besten schätzen wir die Wirkung der dissipativen Kraft, indem wir die
übertragene Arbeit im Fall λ 6= 0 betrachten. Die in einer Periode absorbierte
Energie ist
Aւ
λ6=0 = −f · b · γ
Z
= −f · b · γ
τ
0
Z
cos γt · (sin γt · cos δ + cos γt · sin δ) =
τ
0
t
cos2 γt · sin δ = −f · b · γ cos2 γt sin δ
| {z }
1
τ
2
f
· b · γ · τ | sin δ| > 0 !
2
Die entsprechende absorbierte Leistung ist
⇔ Aւ
λ6=0 =
Aւ . ւ f
= L = γb| sin δ|
τ
2
Dieses Resultat wollen wir in der Nähe der Resonanzfrequenz veranschaulichen (λ ≪ ω0 , γ ≈ ω0 ):
f
γb| sin δ|
2
tan δ
1
·f ·γ · √
=
2
1 + tan2 δ
1
f 2λ
≃
4m (ω0 − γ)2 + λ2
Lւ =
Der letze Ausdruck enthält die Lorentzfunktion, die in der Figur abgebildet ist. Sie ist eine für Resonanzphänomene typische Funktion und kommt
deshalb in der Physik oft vor.
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
25
Abbildung 2.4: Absorbierte Leistung
Im eingeschwungenen Zustand bleibt die Energie eines Systems, das erzwungene Schwingungen ausführt, unverändert. Das System absorbiert allerdings ununterbrochen Energie (aus der Quelle der äusseren Kraft), die infolge
der Reibung dissipiert. Bei der Resonanzfrequenz ist die aufgenommene Leistung maximal, die scharfe Resonanzlinie bekommt eine endliche Breite. In
der Technik führt man oft zur Charakterisierung der Schärfe einer Resonanzlinie den sog. Q-Faktor als Q = Resonanzf requenz/Breite der Resonanzkurve ein. Da Resonanzerscheinungen eine sehr wichtige Rolle in der Natur
spielen und fast in allen Gebieten der Physik vorkommen, wollen wir einige
davon besprechen.
2.8
2.8.1
Resonanzphänomene
Elektrische Resonanzkreise
Ein einfacher elektrischer Resonanzkreis (oder Schwingungskreis) besteht aus
einer Serienschaltung einer Kapazität C, einer Induktivität L und eines
Widerstandes R, hier abgebildet. Die veränderliche Grösse im elektrischen
Schwingkreis ist die transportierte Ladung q in Analogie zu x bei der me-
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
26
chanischen harmonischen Schwingung. Die Schwingungsgleichung für obigen
elektrischen Kreis lautet
1
1
R
· q − · V0 · cos ω0 t = 0
q̈ + · q̇ ·
L
C ·L
L
Die Halbwertsbreite der Resonanzkurve beträgt in diesem Fall R/L. Vergleichen wir die beiden Differenzialgleichungen für u und q, so können wir eine
rein formale Beziehung entsprechender Grössen finden, die in dieser Tabelle
aufgezählt sind.
Charakteristika
Unabhängige Veränderliche
Abhängige Variable
Trägheit
Dämpfung
Resonanzfrequenz (Eigenfreq.)
Schwingungsdauer (Periode)
Q-Faktor
2.8.2
Mech. System
t
x
m
2λ q
k
ω0 = m
q
τ = 2π m
k
ω0
2λ
Elektr. System
t
q
L
R
L
q
1
ω0 = L·C
√
τ = 2π L · C
ω0 ·L
R
Spektroskopien
Man kann die Wechselwirkung zwischen einem System mit atomarer Ausdehnung und elektromagnetischer Strahlung durch eine klassische erzwungene Schwingung simulieren, indem man die von aussen angelegte Störkraft
mit dem elektrischen Feld der Strahlung identifiziert. Systeme mit atomarer
Ausdehnung sind durch diskrete Energiewerte charakterisiert, d.h. dürfen
nur bestimmte Energiewerte annehmen. Die ”Eigenfrequenz” ω0 stellt eine charakteristische Frequenz des Systems dar, und zwar ist sie ein Mass
.
für den Abstand zwischen zwei Energieniveaus, ω0 = (E1 − E0 )/h̄, wobei
h
h̄ = 2π
= 1.054 · 10−34 kg · m2 /s das Plank’sche Wirkungsquantum ist.
Nur bei der Resonanzfrequenz kann das System Energie absorbieren. Diese
Absorption erfolgt durch den Übergang des Systems vom niedrigen Energieniveau E0 zum angeregten Zustand E1 . Durch diese Resonanzerscheinung entsteht die Möglichkeit, die Energieniveaus eines Systems zu bestimmen: das ist
die Grundlage der Spektroskopie, da es ermöglicht, verschiedene Systeme anhand deren Absorpsionsspektren zu erkennen. Mögliche angeregte Zustände
eines Moleküls sind Schwingungen, für welche ω0 mit der klassischen Schwingungsfrequenz übereinstimmt. Schwingungen führen zur Absorption im Infrarotbereich: man sprich von Infrarotspektroskopie. Ein typisches Absorptionsspektrum verursacht durch Schwingungen, ist in der Figur aufgezeichnet.
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
27
Die transmittierte Lichtintensität als Funktion der Wellenlänge des einfal-
lendes Lichts zeigt ein deutliches Transmissionsminimum, entsprechend einer Energieaufnahme der Moleküle, also einer Anregung von Schwingungen.
Solche Minima sind charakteristisch für die betreffende Substanz, und der
Chemiker kann daraus die Natur und Art der zu untersuchenden Probe bestimmen. Absorption im Ultravioletten deutet auf elektronische Anregungen
hin, wie der Übergang zwischen zwei Energieniveaus im Wasserstoffatom. Die
”Natriumflamme” ist ein typisches Beispiel einer elektronischen Anregung.
Das Na-Atom besitzt in seiner elektonischen Struktur zwei benachbarte Niveaus, deren Abstand gelbem Licht entspricht. Auf ein Drahtnetz, das in
der Flamme eines Bunsenbrenners steht, wird Kochsalz gestreut, und die
Flamme leuchtet gelb, entsprechend der Wellenlänge des gelben Na-Lichtes
5890 Å. Durch das Erhitzen werden einige Atome in einen angeregten Zustand versetzt. Die angeregten Atome bleiben jedoch nur sehr kurze Zeit
τ ≈ 10−8 sec in diesem angeregten Zustand und fallen wieder auf ihr Ausgangsniveau zurück. Dabei emittieren sie Licht mit der charakteristischen NaWellenlänge. Beleuchten wir die Flamme mit einer Natrium-Spektrallampe,
die genau diese Wellenlänge emittiert, so beobachten wir an der bestrahlten
Stelle der Flamme auf einem dahinter aufgestellten Schirm schwarze Zonen.
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
28
Durch das Einstrahlen der Resonanzfrequenz ω0 werden die Atome energe-
tisch in den angeregten Zustand versetzt. Ein Teil des einfallenden Lichts wird
für diesen Prozess benutzt, und verschwindet. Das durch spontane Emission reemittierte Licht geht in jeden Raumwinkel und fehlt daher zu einem
hohen Prozentsatz in der Durchstrahlrichtung: ein Schatten entsteht. Aufgrund der endlichen Lebensdauer, besitzen die Niveaus eine gewisse Breite
∆E = h̄/τ : auch benachbarte Frequenzen können am Resonanzprozess teilnehmen. In der Tabelle sind die charakteristischen Absorptionsbereiche, mit
den entsprechenden Anregungen, zusammengefasst.
Spektralgebiet
Ultra-violett (UV)
Infrarot (IR)
Mikrowellen
Art der Anregung
Schwingungen der Valenzelektronen
Molekülvibrationen
Molekülrotationen
Die Absorptionsmaxima im UV einiger typischer organischer Substanzen
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
29
mit Mehrfachbindungen sind im Folgenden aufgezählt.
Verbindung
H2 C = CH2
HC ≡ CH
HC ≡ N
(CH3 )2 C = O
2.8.3
Wellenlänge des Absorptionsmaximums
1625Å
1775Å
1750Å
1870Å
Resonanzen in der Teilchenphysik
Schiesst man z.B. Neutronen auf Iridiumkerne oder π-Mesonen auf Protonen,
so können für sehr kurze Zeiten sog. Resonanzen entstehen, kurzlebige Kombinationsteilchen, die kurz nach ihrer Bildung zerfallen. Das Auftreten einer
Resonanz äussert sich in der Abhängigkeit der Wahrscheinlichkeit σ für eine
bestimmte Reaktion von der Energie: Aus der Breite der Resonanzabsorption, welche gleich h̄/τ ist, liest man die Lebensdauer τ des Kombinationsteilchens ab. Das zeigt, dass Resonanzen auch in der Kern-und Teilchenphysik
von Bedeutung sind: neue Teilchen zeigen sich oft nur als Resonanz in einem
Streuexperiment.
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
2.9
30
Allgemeine Lösung 1-dimensionaler Probleme
In einer Dimension ist die Newtonsche BGL exakt integrierbar, solange
K(x) = − dU
. Wir wollen die Integrierbarkeit beweisen. Aus mẍ = − dU
dx
dx
folgt
ẋ · mẍ = ẋ · (−
dU
)
dx
d[ 21 mẋ2 ]
dU
= −
dt
dt
d[ 21 mẋ2 + U(x)]
= 0
dt
1
.
mẋ2 + U(x) = E
2
Die so gewonnene Integrationskonstante E ist ein Integral der Bewegung, da
sie mit der Zeit unverändert bleibt. Diese Konstante heisst totale Energie der
Bewegung. Sie kann dazu benutzt werden, um die Bewegungen zu klassifizieren. Die resultierende DGL erster Ordnung lässt sich durch Trennung der
Veränderlichen integrieren:
1
mẋ2 + U(x) = E
2
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
dx
=
dt
31
s
2
[E − U(x)]
m
r Z
m
dx
q
+ Konst.
t =
2
E − U(x)
Etwas Allgemeines lernen wir aus dieser Lösung: eine reelle (und somit
physikalische) Lösung existiert nur im Gebiet, wo E > U(x) ist. Diese Gebiete kann man direkt ablesen, wenn man die potentielle Energie graphisch
darstellt. Die Punkte, bei denen E = U(x) ist, sind Umkehrpunkte der Bahn,
Abbildung 2.5: Graphische Darstellung von U(x)
da in ihnen die Geschwindigkeit 0 wird, und sich somit das Vorzeichen ändern
kann. Man unterscheidet zwischen endlichen Bahnen, die in einem endlichen
Raumgebiet verlaufen können, und unendlichen Bahnen, wenn die Masse
ins Unendliche laufen kann. Die eindimensionalen endlichen Bahnen sind
Schwingungen: die Masse bewegt sich zwischen den Umkehrpunkten x1 (E)
und x2 (E) periodisch, d.h. sie kehrt nach einer gewissen Zeit wieder an einen
bestimmten Punkt zurück. Die Periode der Schwingung ist durch den Ausdruck
r Z x (E)
m 2
dx
q
T (E) = 2 ·
2 x1 (E)
E − U(x)
gegeben. Wir diskutieren, als beispiel, den Fall von kleinen Schwingungen.
Dann
U ′′ (x0 )
U(x) = U(x0 ) + (x − x0 )2
2
und aus
′′
U(x0 ) + (xi − x0 )2 U 2(x0 )
= E folgt xi (E) = x0 ±
setzt in den Ausdruck für T (E) ergibt dies
T (E) = 2 ·
r
r
2(E−U (x0 ))
.
U ′′ (x0 )
m Z x2 (E)
dx
q
′′
2 x1 (E)
E − U(x0 ) − (x − x0 )2 U 2(x0 )
Einge-
KAPITEL 2. EINDIMENSIONALE MECHANIK: BEISPIELE
= 2·
s
m
′′
U (x0 )
= 2·
s
U ′′ (x0 )
= 2π
s
m
Z
q
−
2(E−U (x0 ))
U ′′ (x0 )
q
−2(E−U (x0 ))
U ′′ (x0 )
32
dy
q
2(E − U(x0 )/U ′′ − y 2
· [arcsin(1) − arcsin(−1)]
m
U ′′ (x0 )
Wie früher schon bewiesen, ist T von E unabängig. Dies ist aber nur in
der harmonischen Näherung gültig. Für die Schwingung definiert man ei.
ne Schwingungsfrequenz als ω = 2π
. In der harmonischen Näherung ist
T
q
′′
ω = Um . Die Frequenz ist das fundamentale Charakteristikum von Schwingungen; sie hängt nicht von den Anfangsbedingungen der Bewegung ab,
sondern ist vollständig durch die mechanische Eigenschaft des Systems bestimmt. Im Wesentlichen gibt sie Auskunft über die Krümmung (zweite Ableitung!) der potentiellen Energie in der Nähe der Ruhelage. Dieses Resultat
ist von entscheidender Bedeutung für die Spektroskopie von Molekülen und
Festkörpern: durch die spektroskopische Bestimmung der Schwingungsfrequenz lässt sich etwas über die potentielle Energie der Moleküle aussagen!!
Kapitel 3
1d Schwingungen mit mehreren
Freiheitsgraden
Mit unserem mechanischen Modell können wir die Schwingungen einer Masse
erfassen, die entlang einer Koordinate harmonische Oszillationen durchführt.
Die rücktreibende Kraft bietet eine Feder mit der Federkonstante k = U ′′ (x0 )
(x0 : Gleichgewichstlage). Wir wollen jetzt mit dem gleichen Federmodell versuchen, die Bewegung mehrerer, durch Feder gekoppelter Massen zu erfassen.
Wir beginnen mit einem einfachen Beispiel.
3.1
Eigenmode zweier gekoppelter harmonischer Oszillatoren
Wir betrachten zwei identische Massen, die durch eine Feder mit der Federkonstante k gekoppelt sind. Jede Masse ist mit einer weiteren Feder (auch
mit Federkonstante k) an einer festen Wand gebunden. Im Gleichgewicht besetzen die Massen Gitterpunkte mit Gitterkonstante a (in Molekülen ≈ 0.1
nm). Die Abweichungen der i-ten Masse aus der Ruhelage bezeichen wir mit
ui (in Molekülen ≈ 0.01 nm).
mü1 = −k · u1 − k · (u1 − u2 )
mü2 = −k · u2 − k · (u2 − u1 )
Es handelt sich, mathematisch gesehen, um ein lineares gekoppeltes Differentialgleichungssystem. Die Kopplung äussert sich mit der Tatsache, dass
die Bewegung der 1. Masse durch die Lage der 2. Masse beeinflusst wird,
und umgekehrt. Somit sind die beiden Massen nicht unabhängig. Wir suchen
33
KAPITEL 3. 1D SCHWINGUNGEN MIT MEHREREN FREIHEITSGRADEN34
nach der allgemeinen Lösung als die lineare Superposition von Fundamentallösungen, die Eigenmoden genannt werden. Dieses Superpositionsprinzip
stammt aus der Tatsache, dass die DGL linear sind. Der Eigenmodenansatz
lautet:
ui = ai · eiωt
d.h. wir suchen nach Lösungen, in deren beide Massen mit der gleichen,
zu bestimmenden Frequenz ω oszillieren. Für die (komplexe) Amplitude ai
versuchen wir, algebraische Gleichungen zu etablieren. Das geschieht durch
Einsetzen des Eigenmodenansatzes in das DGL-System. Es resultiert ein homogenes Gleichungssystem für die unbekannten Amplituden a1 , a2 . In Matrixschreibweise:
!
−mω 2 + 2k
−k
−k
−mω 2 + 2k
a1
a2
!
=
0
0
!
Eine triviale Lösung ist der Grundzustand u1 = u2 = 0. Endliche Amplituden erhält man, nur wenn die Determinante der Matrix verschwindet. Das
ergibt die Determinantengleichung (oder charakteristische Gleichung) für die
zu bestimmende Eigenfrequenz ω:
(2k − mω 2 )2 − k 2 = 0
Nur eine endliche Anzahl Frequenzen bilden die Lösung der Determinantengleichung: d.h. nur bei ausgewählten Frequenzen können sich Eigenmoden
entwickeln. In diesem Fall finden wir die zwei möglichen Eigenfrequenzen
k
m
3k
=
m
ωα2 =
ωβ2
Setzen wir ωα in das Gleichungssystem, erhalten wir die Lösung a1 = a2 .
Diese Eigenmode (1, 1) besagt, dass beide Massen zu jeder Zeit die gleiche
Auslenkung besitzen, und zwar gleiche Amplitude und gleiches Vorzeichen.
Sie sind genau in Takt. Zu ωβ gehört der Eigenmode (1, −1): in dieser Eigenmode schwingen die Massen mit gleicher Amplitude aber entgegengesetzten
Vorzeichen und sind um eine Phase π ausser Takt. Zusammenfassend: die
gesuchten Eigenmoden sind
iωα t
1
1
!
iωβ t
1
1̄
!
uα (t) = e
uβ (t) = e
KAPITEL 3. 1D SCHWINGUNGEN MIT MEHREREN FREIHEITSGRADEN35
Somit lautet die allgemeine Lösung:
u1 (t)
u2 (t)
!
=
cα eiωα t + cβ eiωβ t
cα eiωα t − cβ eiωβ t
!
Eine moderne Anwendung dieser Anordung findet man in der Atomkraftmikroskopie (AFM). Für die Interpretation der Messungen in AFM benutzt
man oft ein Modell, in welchen Oberflächenatome, die durch ”eine Feder” am
Kristall gebunden sind, die Kraft einer naheliegenden Spitze als eine zusätzliche Feder spüren. Die Spitze selbst ist an einem schwingenden Balken festgebunden. Nur bei bestimmten Frequnzen ist es möglich, Schwingungen des
gekoppelten Systems ”Atom-Spitze” anzuregen. Diese Resonanzfrequenzen
liefern, nach nach unseren Überlegungen, unmittelbare Informationen über
die an der Bindung beteiligten Kräfte. Diese Resonanzen werden sogar für
den Transport der Atome von einer Stelle zur anderen benutzt.
3.2
Eigenmode einer schwingenden Kette
mit N -gekoppelten Oszillatoren
Wir betrachten eine lineare Kette von N Atomen der Masse m entlang der
x-Koordinate. Die Atome sind paarweise mit einer Feder (Federkonstanten
.
k) gekoppelt. Wir bezeichnen als u(n) = xn −n·a die Abweichung der n−ten
Masse aus der Ruhelage n · a, wobei a die Gitterkonstante ist. Die BG für
Abbildung 3.1:
die n − te Masse lesen wir aus der Figur ab:
mü(n) = k[u(n − 1) + u(n + 1)] − 2ku(n)
Da die Auslenkungen u(n ± 1) in der BGL für das n − te Atom auftreten,
bilden alle BGL ein System von N gekoppelten DGL. Die Lösung hängt davon
ab, welche Randbedingungen der Kette auferlegt werden. Man kann z.B. die
KAPITEL 3. 1D SCHWINGUNGEN MIT MEHREREN FREIHEITSGRADEN36
Randatome festhalten oder frei geben. Wenn n eine kleine Zahl ist, hängen
die Lösungen stark von diesen Randbedingungen ab (siehe Übungen). Bei
einer makroskopischen Anzahl N muss der Einfluss der Randbedingungen auf
die Schwingungsfrequenzen klein sein. Physikalisch kann man sich vorstellen,
dass die Kette zu einem Kreis gebogen wird, wobei am N-ten Atom noch
eine Feder angebracht ist, die es mit dem ersten Atom verbindet. Damit hat
man den Rand eliminiert. Mathematisch bedeutet diese Biegung der Kette
zu einem Kreis die Annahme periodischer (in der Fachliteratur auch Bornvon Karman) Randbedingungen: u(n) = u(n + N). Die Lösungen des DG
Systems mit diesen Randbedingungen sind solche, die der Realität näher
kommen sollten, weil sie Oberflächeneffekte auf die Festkörpereigenschaften
eliminieren. Zur Lösung des DG Systems macht man den Eigenmoden-Ansatz
u(n) = an · eiωt
Die Amplitude an können wir durch folgende Überlegungen näher festlegen.
Wie im vorigen Beispiel gezeigt, brechen einige Eigenmode die Translationssymmetrie des Systems, die dem Grundzustand einer in sich geschlossenen
Kette von Gitterpunkten zugrunde liegt. Das bedeutet: ai 6= aj . Wir erwarten trotzdem, dass mindestens | ai |=| aj |, wobei wir | ai |= 1 setzen dürfen,
o.E.d.A. Somit befinden sich die gesuchten Amplituden auf dem Einheitskreis in der komplexen Ebene. Wir parametrisieren die Amplituden nach
dem (plausiblen) Ansatz
an = eiq·n·a
wobei q ein zu bestimmender reeller Parameter ist. Durch Einsetzen des
Eigenmodenansatzes wird n eliminiert und resultiert die charakteristische
Gleichung
−mω 2 = k[e−iqa + eiqa − 2] = 2k[cos(qa) − 1]
deren Lösung die möglichen Eigenfrequenzen q
der schwingenden Kette ergibt,
in Abhängigkeit des Parameters q: ω(q) = 2 k/m · sin(qa/2) Die Randbedingung bestimmt die möglichen Werte des Parameters q: eiq(n+N )a = eiqna ,
d.h. eiqN a = 1 oder qNa = p · 2π, p = 0, 1, 2, ....., N − 1. Die möglichen
Schwingungszustände sind durch dicht nebeneinanderliegende q-Werte klassifiziert, jeder q-Wert trägt eine bestimmte Eigenfrequenz. Die gesuchten N
linear unabhängigen Lösungen können durch die q-Werte im Intervall 0, 2π/a
dargestellt werden. (gelegentlich benutzt man den Intervall [−π/a, π/a], um
die Eigenfrequenzen
darzustellen). Die Kopplung bewirkt, dass sich die Freq
quenz k/m des ungekoppelten Oszillators zu einem Frequenzband verbreitet. Jeder Frequenz kann ein q-Wert zugeordnet werden. Die q-Abhängigkeit
von ω nennt man Dispersionsrelation. Die Lösungen der BGL nennt man
KAPITEL 3. 1D SCHWINGUNGEN MIT MEHREREN FREIHEITSGRADEN37
Abbildung 3.2:
Eigenmode, die zu den Eigenfrequenzen ω(q) gehören. In der Quantenmechanik nennt man diese Eigenmode Phononen. Besteht die Kette aus Atomen
mit unterschiedlichen alternierenden Massen, erwartet man mindestens zweiPhononenbänder, die evtl. durch eine Lücke getrennt sind. Verbindungen wie
NaCl haben zum Beispiel zwei Phononenbänder: Das untere Band nennt man
akustisches Phonon, das obere sind die optischen Phononen. Einen optischen
und akustischen Zweig bekommt man auch, wenn die Kraftkonstanten alternierend sind. Diese Resultate lassen sich auf dreidimensionale Kristalle
erweitern. In drei Dimensionen, wird q zu einem Vektor, der innerhalb eines
Polyeders verteilt ist. Die Phononendispersionsrelationen können richtungsabhängig werden und einen komplizierteren Verlauf zeigen.
3.3
Übergang zum schwingenden Kontinuum: Die Wellengleichung
Wir betrachten Phononen mit q ≈ 0. Für solche Phononen ist die charakteristische Länge λ über welche q · n · a ≈ O(2π) sehr gross (λ ∝ 2π/q).
Das bedeutet: die Auslenkungen benachbarter Atome sind nur infinitesimal
unterschiedlich, a kann als infinitesimal klein betrachtet werden und n · a
können wir als kontinuierliche Variable betrachten. Die BGL für die skalare
Funktion u(x, t) kann man folgendermassen aufstellen:
m
∂2u
= k[u(n − 1, t) + u(n + 1, t)] − 2ku(n, t)
∂t2
a2
≈ k[u(n, t) − au′ (n) + u′′ (n) + u(n, t)
2
2
a
+ au′ (n) + u′′ (n)] − 2ku(n, t)
2
2
∂
u
= ka2 2
∂x
KAPITEL 3. 1D SCHWINGUNGEN MIT MEHREREN FREIHEITSGRADEN38
Abbildung 3.3:
∂2u
ka2 ∂ 2 u
=
∂t2
m ∂x2
Da wir mit einer Funktion mehrerer Variablen zu tun haben, müssen wir den
Begriff der partiellen Ableitung einführen:
∂u .
u(x + ∆x, t) − u(x, t)
= lim
∂x ∆x→0
∆x
(und ähnlich für t). Somit werden bei der partiellen Ableitung nach einer
Variablen die anderen Variablen als Konstanten betrachtet. Mit dieser Definition bekommt die BG für u(x, t) eine eindeutige Bedeutung. Die Material2
konstante ka
wird als c2 bezeichnet. Ihre Bedeutung wird bald klar. Diese
m
Gleichung ist die eindimensionale Wellengleichung: sie ist die Bewegungsgleichung für die Auslenkung u an der Stelle x zur Zeit t. Es ist eine partielle
lineare DGL 2-ter Ordnung: sie enthält sowohl die 2-te Ableitung nach der
Zeit als auch die zweite Ableitung nach x.
Theorem (D’ Alembert): die allgemeine Lösung der 1-dim. Wellengleichung ist
u(x, t) = f (x − ct) + g(x + ct)
KAPITEL 3. 1D SCHWINGUNGEN MIT MEHREREN FREIHEITSGRADEN39
Um diese Lösung darzustellen, stelle man sich eine lokale Störung f (x, t = 0)
vor, die zum Beispiel ein Maximum bei x0 besitzt. Eine solche Störung kann
zum Beispiel eine Verschiebung der Teilchen eines Mediums aus ihrer Ruhelage (Phononen, Seilwellen, Wasseroberflächenwellen) oder einer Dichteschwankung bei elastischen Wellen, Schallwellen und Erdbebenwellen bedeuten. Es
kann aber ein elekromagnetisches Feld (Licht) bedeuten, das sich durch ein
plötzliches Ein- und Ausschalten eines Stromes gebildet hat. Wenn diese
Abbildung 3.4:
Störung nach der Wellengleichung evolviert, ist die funktionelle Abhängigkeit zur Zeit t f (x − ct), siehe Figur, d.h. die Störung sieht genau gleich aus
wie zur Zeit t = 0 aber ist am Ort xt = ct + x0 zentriert: die Wellengleichung hat die Störung fortgepflanzt, und zwar mit Beibehaltung der Form.
Die Materialkonstante c ist die Fortpflanzungsgeschwindigkeit. Die Lösung
f (x + ct) beschreibt eine Welle, die sich nach links entlang der x-Achse fortpflanzt. Die Materialkonstanten,
die c bestimmen, hängen von der Wellenart
q
(ρ
=m
die Masse pro Längeneinheit). k · a ist
ab. Bei Phononen ist c = ka
ρ
a
ein Mass für die mittlere rücktreibende Kraft, die von einer Feder ausgeübt
wird. Bei der schwingenden Seite (Seilwellen) erfolgt die Auslenkung u(x, t)
senkrecht zur Koordinaten x und die rücktreibende Kraft ist die Zugkraft,
mit welcher das Seil gespannt wird. Daraus ergibt sich, dass die Geschwindigkeit von Seilwellen proportional
q zur Wurzel der Zugkraft ist. Bei Schallwellen
und Erdbebenwellen ist c = E/ρ, E: Elastizitätsmodul. Auch Licht – d.h.
elektromagnetische Felder – pflanzen sich nach der Wellengleichung fort, und
zwar mit Lichtgeschwindigkeit.
Wir beweisen die D’ Alembertsche Lösung durch explizites Einsetzen in
KAPITEL 3. 1D SCHWINGUNGEN MIT MEHREREN FREIHEITSGRADEN40
die Wellengleichung. Als Beispiel betrachten wir die Lösung mit Argument
.
∂
≡ ∂α ).
x − c · t = ξ ( ∂α
∂t ∂t f (x − c · t) = ∂t ∂ξ f (ξ) · (−c)
= ∂ξ ∂ξ f (ξ) · (c) · (−c)
= c2 · ∂ξ ∂ξ f (ξ)
Anderseits gilt
c2 ∂x ∂x f (x − c · t) = c2 ∂ξ ∂ξ f (ξ)
Somit ist die linke Seite der Gleichung identisch mit der rechten und f (x−c·t)
erfüllt die Wellengleichung. Entscheidend für diesen Beweis ist das Argument
der Funktion: die Variablen x und t dürfen nicht in beliebige Zusammensetung vorkommen
3.3.1
Die harmonische Welle
Die harmonische Welle f (x, t) = A · cos(q · x − ωt) erfüllt die WG, wenn
ω = c · q. Diese ist die Dispersionsrelation, die wir für langwellige Phononen
aus der exakten Lösung erwartet haben. Eine instantane Aufnahme einer
harmonischen Welle erlaubt, die verschiedenen Parameter zu veranschauli.
chen: λ = 2π/q ist der Abstand zweier Wellentäler (oder analoge Punkte der
Abbildung 3.5: Harmonische Welle zu einer festen Zeit (links) und an einem
bestimmten Ort (rechts)
Welle) und heisst Wellenlänge. q ist die Wellenzahl und gibt gerade die Zahl
der Wellentäler pro Längeneinheit an. Man betrachte jetzt den zeitlichen
Ablauf an einem festen Ort, nach der Zeit T wiederholt sich in x dieselbe
Phase der Welle, z.B. ein Wellental: T ist die Periode der Welle. ω = 2π/T
ist dann die Frequenz, mit welcher sich dieselbe Phase pro Zeiteinheit
wiederholt. Es gilt: λ = cT .
KAPITEL 3. 1D SCHWINGUNGEN MIT MEHREREN FREIHEITSGRADEN41
3.3.2
Die stehende Welle
Eine von links einfallende harmonische Seilwelle trifft auf eine feste Halterung (aber es kann sich auch um eine ebene Lichtwelle handeln, die an einem
Spiegel reflektiert wird) bei x = 0. Die Gesamtwelle setzt sich aus der einfallenden und der reflektierten Welle zusammen, wobei die Randbedingung
u(x = 0, t) = 0 ∀t erfüllt werden muss. Die gesuchte Lösung ist
u(x, t) = A[cos(ωt − qx) − cos(ωt + qx)]
= 2A sin qx sin ωt
Wie die Figur zeigt, ist das keine normale laufende Welle mehr: Es gibt
nämlich Schwingungsknoten, an denen die Welle immer verschwindet, und
es gibt Schwingungszeiten an denen die Auslenkung überall verschwindet.
Da die Schwingungsknoten eine feste Lage im Raum haben, spricht man von
einer stehenden Welle. Die Schwingungsknoten sind durch die Gleichung
sin qxn = 0 bestimmt, d.h. |xn | = nλ/2, n = 0, 1, 2, 3....
Abbildung 3.6: Stehende Welle (links) und Resonator (rechts)
3.3.3
Eigenfrequenzen eines schwingenden Seils
Hält man das Seil auch noch im Abstand L fest, so tritt die zusätzliche
Randbedingung sin qL = 0 auf, die nur für bestimmte q- Zahlen (d.h. für bestimmte Wellenlängen) erfüllbar ist: λn = 2L/n, n = 0, 1, 2, ... Dies bedeutet,
dass die stehende Welle im Gebiet L nur bestimmte Frequenzen ωn = nπc
L
annehmen darf: die Eigenfrequenzen eines Seils. Stehende Wellen liegen fast
allen Musikinstrumenten zugrunde: es ist damit möglich, bestimmte Noten zu
selektieren. Wenn wir an Licht denken, das zwischen zwei Spiegeln reflektiert
wird, so können wir uns genauso vorstellen, dass nur bestimmte Frequenzen
und Wellenlängen zwischen den zwei Spiegeln existieren können. In diesem
KAPITEL 3. 1D SCHWINGUNGEN MIT MEHREREN FREIHEITSGRADEN42
Fall spricht man von einem optischen Resonator. Ein solcher optischer Resonator ist eine fundamentale Komponente für die Erzeugung von Laserlicht,
das sehr genau monochromatisch ist.
Kapitel 4
Mechanik im euklidischen
Raum
Die Formulierung der Newtonschen BGL im dreidimensionalen Raum erfordert die Einführung des Vektorbegriffs und die Begriffe der Skalar- und
Vektorfelder.
4.1
Vektoralgebra
Verschiedene Grössen in der Physik, wie zum Beispiel die Grundgrössen Länge, Masse
und Zeit, können im Rahmen der Newtonschen Mechanik durch eine einzige reelle Zahl
spezifiziert werden. Diese Zahl kann dabei von dem Einheitensystem abhängen, in dem wir
die Messung vornehmen. Solche Grössen bezeichnen wir als Skalare. Ein Skalar wird durch
einen Buchstaben angegeben, z.B. für die Zeit t und für die Masse m. Andere Grössen in
der Physik, wie die Ortsangabe oder die Geschwindigkeit bedürfen zu ihrer vollständigen
Spezifikation der Angabe eines Betrages und einer Richtung. Solche Grössen nennen wir
Vektoren und kennzeichnen sie durch einen Pfeil über den Buchstaben, um die Bedeutung
der Richtungsangabe hervorzuheben. Den Betrag oder die Länge eines Vektors bezeichnen
wir mit ~a mit |~a| oder a.
Rechnenregel
Die Rechnenregel der Vektoralgebra sind hier zusammengefasst:
• −~a bezeichnet einen Vektor, der die gleiche Länge wie der Vektor ~a aufweist, aber
in die entgegengesetzte Richtung zeigt
• Vektoraddition und Kommutativität. Der Summenvektor ~a + ~b beginnt am Fusspunkt von ~a und reicht bis zur Spitze von ~b (~a + ~b entspricht der Diagonalen des
von ~a und ~b aufgespannten Parallelogramms) : ~a + ~b = ~b + ~a
• Assoziativität: (~a + ~b) + ~c = ~a + (~b + ~c).
• ~a −~b = ~a +(−~b) (~a −~a = ~0 der Nullvektor, mit Betrag 0 und richtungslos: ~a +~0 = ~a).
• p~a (p = reelleZahl) hat die gleiche Richtung wie ~a und |p~a| = |p| · |~a|
43
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
44
• (p + q)~a = p~a + q~a, p(~a + ~b) = p~a + p~b, q(p~a) = p(q~a) = qp~a
• Ein Einheitsvektor ist ein Vektor mit der Länge 1. Aus jedem Vektor ~a lässt sich
durch Multiplikation mit dem Kehrwert seines Betrages ein Einheitsvektor ~ea in
Richtung von ~a konstruieren. ~ea = a1 ~a. Einheitsvektoren werden in der Regel mit
den Buchstaben ~e oder ~n bezeichnet.
• Die Menge der Vektoren mit den o.g. Rechnenregel bildet ein Vektorraum.
• Der Skalarprodukt zweier Vektoren ~a und ~b bezeichnet man den folgenden Skalar:
~a · ~b = ab cos ϑ wobei ϑ den Winkel zwischen den Vektoren ~a und ~b bezeichnet.
• Zwei Vektoren ~a und ~b sind orthogonal (~a ⊥ ~b) zueinander, falls ~a · ~b = 0.
√
• Wegen cos(0) = 1 gilt ~a · ~a = a2 ≥ 0 oder a = ~a · ~a
• Für den Einheitsvektor haben wir ~e · ~e = 1
• Ein Vektorraum, in dem ein Skalarprodukt definiert ist, heisst Vektorraum mit
Skalarprodukt.
• Zwei Vektoren ~a und ~b mit der selben Richtung ~e sind linear abhängig (kolinear):
es existieren zwei zahlen alpha und β so dass α~a + β~b = 0
• Zwei Vektoren ~a und ~b heissen linear unabhängig, falls die Gleichung α~a + β~b = 0
nur durch α = β = 0 erfüllt werden kann.
• Ferner gilt die Definition: Die Dimension eines Vektorraumes ist gleich der maximalen Anzahl linear unabhängiger Vektoren
• In einem d-dimensionalen Vektorraum bildet jede Menge von d linear unabhängigen Vektoren eine Basis, d.h. jeder beliebige Vektor dieses Raumes lässt sich als
Linearkombination dieser d Vektoren beschreiben.
• Einheitsvektoren ~ei , i = 1, 2, ..., d., die paarweise orthogonal zueinander sind, bilden
ein Orthonormalsystem: ~ei · ~ej = δij mit dem Kronecker-Symbol
1 für i = j
δij =
0 für i 6= j .
• Für einen beliebigen Vektor ~a gilt ~a =
d
P
aj ~ej Die aj sind die Komponenten des
j=1
Vektors ~a bezüglich der Basis ~e1 , ..., ~ed . Beispielsweise bilden die kartesischen Basisvektoren ~ex , ~ey und ~ez ein vollständiges Orthonormalsystem des Euklidischen
Raumes E3
• Für den dreidimensionalen euklidischen Raum können
 wirsomit explizit schreiben
x
~r = x~ex + y~ey + z~ez oder (als Spaltenvektor) ~r =  y  und Zeilenvektor ~r =
z
(x, y, z)
• Das Skalarprodukt lässt sich mit dem vollständigen Orthonormalsystem leicht auswerten. Es ist
X
ai b i
~a · ~b =
i
Somit ist der Betrag eines Vektors
pP
i
a2i .
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
45
• Einem Produkt von zwei Vektoren können wir auch einen Vektor zuordnen. Das
Vektorprodukt von zwei Vektoren ~a und ~b führt zu einem Vektor ~c = ~a × ~b
• | ~c |=| ~a || ~b | · sin ϑ (ϑ ist der von ~a und ~b eingeschlossene Winkel). Der Betrag von
~c, also c, entspricht dem Flächeninhalt des von ~a und ~b aufgespannten Parallelogramms.
• ~c steht senkrecht auf der von ~a und ~b aufgespannten Ebene. ~a, vecb und ~c bilden
ein Rechtssystem.
• antikommutativ: ~a × ~b = −~b × ~a
• ~a × ~b = 0 bedeutet, dass die Vektoren parallel sind (oder ein Vekrot der Nullvektor
ist).
• distributiv: (~a + ~b) × ~c = ~a × ~c + ~b × ~c
• nicht assoziativ ~a × (~b × ~c) 6= (~a × ~b) × ~c
• bilinear (α~a) × ~b = ~a × (α~b) = α(~a × ~b)
•
~e1
~e2
~e3
×
×
×
~e2 = ~e3 ,
~e3 = ~e1 ,
~e1 = ~e2 ,
aber zum Beispiel ~e2 × ~e1 = −~e3 und ~e1 × ~e1 = 0. Somit gilt:
~c = ~a × ~b =
3
X
i,j=1
ai bj (~ei × ~ej ) =
3
X
ck ~ek
k=1
mit
c 1 = a 2 b 3 − a 3 b 2 , c2 = a 3 b 1 − a 1 b 3 , c3 = a 1 b 2 − a 2 b 1 .
• Das Kreuzprodukt lässt sich auch
auswerten.
~e1 ~e2 ~e3
~
~a × b = a1 a2 a3
b1 b2 b3
leicht mit Hilfe der Determinantenschreibweise
= (a2 b3 − a3 b2 )~e1 − (a1 b3 − a3 b1 )~e2 + (a1 b2 − a2 b1 )~e3 .
• Der gemischer Produkt ~a · (~b × ~c) ist ein Skalar (Symbol (~a, ~b, ~c)) stellt das
Volumen von dem durch ~a, ~b und ~c aufgespannetn Parallelogramm. Das zyklische
Permutieren der Vektoren ändert den Wert des GP nicht, Vrtausche zweier Vektoren
bewirkt Multiplikation mit −1.
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
46
Der Begriff des Feldes stellt ein fundamentales Konzept in der Physik dar. Man unterscheidet zwischen Skalarfeldern und Vektorfeldern, welche auf E3 definiert sind. Ein Skalarfeld Φ(~r) = Φ(x, y, z) ist eine skalarwertige Funktion
dreier unabhängiger Variablen.
p
Als Beispiel betrachten wir die Funktion Φ(~r) = α/( x2 + y 2 + z 2 ). Graphisch stellt man
solche Felder durch 2-dimensionale Schnitte dar, in denen die Flächen Φ(~r) = Konst
(Äquipotentialfläche) als Höhenlinien erscheinen. Der Abstand der Linien entspricht dabei gleichen Wertunterschieden der Konstanten. Ein Vektorfeld ordnet jedem Punkt im
~ = K(~
~ r ) zu. Als Beispiel betrachten wir das GraviRaum eine vektorwertige Funktion K
~ r ) = −M γ · 2 2~r 2 3/2 .
tationsfeld eines Massenpunktes (zum Beispiel die Sonne): K(~
(x +y +z )
Graphisch lassen sich Vektorfelder mittels Feldlinien darstellen, wobei das Feld tangential
zur Feldlinie verläuft. Die Dichte der Feldlinien ist dann ein Mass für die Stärke des Feldes.
Abbildung 4.1: Graphische Darstellung von Feldern
Für Skalarfelder kann man den Begriff der partiellen Ableitung einführen:
Φ(x + ∆x, y, z) − Φ(x, y, z)
∂Φ .
= lim
∆x→0
∂x
∆x
(und ähnlich für y, z). Damit lässt sich die räumliche Änderung der Skalarfelder beschreiben. Wir betrachten zwei Punkte ~r1 und ~r2 , die durch eine kleine Strecke d~r voneinander
getrennt sind.
Die Änderung dΦ = Φ(~r2 ) − Φ(~r1 ) ist gegeben durch die folgende Summe:
dΦ
∂Φ
∂Φ
∂Φ
dx +
dy +
dz
∂x
∂y
∂z
∂Φ ∂Φ ∂Φ
= (
,
,
) · (dx, dy, dz)
∂x ∂y ∂z
. ~
= ∇Φ
· d~r
=
~ der Gradient von Φ und dΦ das totale Differenzial des Feldes Φ sind. Der
wobei ∇Φ
Gradient lässt sich deuten, indem man d~r in die Richtung wählt, so dass dΦ = 0 in
~ · dr~0 = 0 folgt, dass ∇Φ
~ senkrecht auf dr~0
dieser Richtung ist. Aus der Gleichung ∇Φ
~ senkrecht auf den
steht. Andererseits definiert dΦ = 0 Flächen Φ = Konst., so dass ∇Φ
Äquipotenzialflächen steht. Sein Betrag ist ein Mass für die Stärke der Änderung von Φ,
wenn man senkrecht zu den Äquipotenzialflächen fortschreitet.
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
47
Abbildung 4.2: Konstruktion zur Berechnung von dΦ (links) und graphische
Deutung des Gradienten (rechts)
4.2
Bewegung eines Massenpunktes im Zentralfeld
Die Verallgemeinerung der BGL im dreidimensionalen Raum ist, aufgrund
der mathematischen Begriffe, die wir bereits eingeführt haben, selbstverständlich. Setzt man kartesische
Koordinaten
voraus, dann ist ~r(t) =
x(t)~ex + y(t)~ey + z(t)~ez ≡ x(t), y(t)z(t) eine vektorwertige Funktion
der Zeit t. Für den Geschwindigkeitsvektor gilt die Vektorableitung
. d~r
˙ =
= ẋ(t)~ex + ẏ(t)~ey + ż(t)~ez
~r(t)
dt
.
Die Beschleunigung ist ~¨r(t) =
Newtonsche Axiom lautet:
d2 ~
r
dt2
= ẍ(t)~ex + ÿ(t)~ey + z̈(t)~ez und das 2.
~ r (t), ~r˙ (t), t)
m~¨r (t) = m · K(~
An der rechten Seite ist ein Vektorfeld, das die eigentliche Dynamik des Massenpunktes bestimmt und sich oft als der negative Gradient eines potentiellen
~ r) = −∇U(~
~ r ).
skalaren Energiefeldes schreiben lässt: K(~
Wir betrachten jetzt als beispiel einen Massenpunkt in einem Zentralfeld.
Ein Zentralkraftfeld wird√durch eines Potential definiert, welche nur vom
.
r =| ~r | abhängt: U = U( x2 + y 2 + z 2 ). Somit ist
q
dU ~r
~
~
K(~r) = −∇U( x2 + y 2 + z 2 ) = −
dr | ~r |
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
48
U(r) ist eine kugelsymmetrische Funktion, welche invariant gegenüber Rotationen um den Ursprung des Koordinatensystems ist. Entsprechend zeigt
~ r) entlang des Vektors ~r. Beispiel von Zentralfeldern ist die von der Sonne
K(~
auf die Planeten ausgeübte Gravitationsfeld. Aber auch das Coulomb-Feld
eines Protons auf dem herumkreisenden Elektron ist ein Zentralfeld.
Die Tatsache, dass das Feld entlang ~r ist, liefert eine wichtige Vereinfachung des drei-dimensionalen Problems eines Teilchens im äusseren Kraftfeld.
Wir bilden die Grösse
m · ~r × ~r˙
Diese Grösse hat auf den ersten Blick keine unmittelbare Bedeutung, aber besitzt die wichtige Eigenschaft, dass sie eine Konstante (oder Integral) der
Bewegung ist. Mit anderen Worten: dieses Vektorprodukt bleibt konstant,
obwohl seine Bestandteile durchaus zeitabhängig sind. Der Beweis zeigt di~ –:
rekt die Quelle dieser Erhaltungsgrösse –des Drehimpuls L
Beweis:
d~
~ ≡0
L = m~r˙ × ~r˙ + m · ~r × ~¨r = 0 + ~r × K
dt
~ zeigt
da, nach unserer Voraussetzung, die Kraft zentralgerichtet ist. L
während der ganzen Bewegung in eine feste Raumrichtung, die wir als die
~ = L0~ez als Vektorprodukt von ~r und ~r˙ konstruiert
z-Achse wählen. Da L
wurde, steht er senkrecht zu diesen beiden Vektoren. Daraus folgt: die Bahn
eines Teilchens in einem zentralgerichteten Kraftfeld liegt vollständig in
~ senkrecht steht und die wir als die x − y Ebene
einer Ebene, die auf L
annehmen können. Den Vektor ~r dürfen wir als zwei-komponentigen Vektor
annehmen, die dazugehörige BGL sind zwei-dimensional.
Es ist zweckmässig, die Polarkoordinaten ρ und ϕ und die orthogonalen Einheitsvektoren ~eρ und ~eϕ einzuführen:
x =
x(ρ, ϕ) = ρ cos ϕ
y
y(ρ, ϕ) = ρ sin ϕ
=
Setzen wir ρ = Konst., dann wird durch Variieren von ϕ eine Kurve (keine Gerade!!!)
beschrieben, die ϕ-Koordinatenlinie. Setzen wir ϕ = Konst., dann erhalten wir eine durch
ρ parametrisierte Koordinatenlinie. (Die gleiche Operation zur Erzeugung von Koordinatenlinien in kartesischen Koordinaten führt zu Geraden, die parallel zur x-bzw. y-Achse
laufen. Deswegen bezeichnet man Polarkoordinaten als ein Beispiel ”krummliniger” Koordinaten). Die BGL für die kartesische Kooridnianten x, y, lauten:
m · ẍ = m · K(x2 + y 2 )
(x2
x
+ y 2)1/2
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
m · ÿ = m · K(x2 + y 2 )
49
y
(x2 + y 2)1/2
Wir transformieren die rechte und linke Seiten der BGL in Polarkoordinaten
x
= cos ϕ
(x2 + y 2 )1/2
y
= sin ϕ
(x2 + y 2 )1/2
ẍ = ¨(ρ · cos ϕ) = ρ̈ cos ϕ − 2ρ̇ϕ̇ sin ϕ − ρϕ̈ sin ϕ − ρϕ̇2 cos ϕ
ÿ = ¨(ρ · sin ϕ) = ρ̈ sin ϕ + 2ρ̇ϕ̇ cos ϕ + ρϕ̈ cos ϕ − ρϕ̇2 sin ϕ
Wir multiplizieren beide DGL mit cos ϕ und addieren sie, beziehungsweise
multiplizieren mit sin ϕ und subtrahieren sie. Daraus folgt
mρ̈ = ·mKρ (ρ) + mρϕ̇2
mρϕ̈ = −2mρ̇ϕ̇
Die Transformation zur Polarkoordinaten hat eine zusätzliche radialgerichtete Kraft eingeführt, die durch die Verwendung von nicht-kartesischen Basisvektoren entstanden ist. Diese zusätzliche radial gerichtete Kraft heisst
Zentrifugalkraft. Sie beeinflusst die radiale Bewegung. Die BGL für ϕ̈ zeigt
die Existenz einer weiteren effektiven Kraft, welche durch die Transformation zur Polarkoordinaten entstanden ist, und welche für die Änderung der
Drehgeschwindigkeit ϕ̇ verantwortlich ist: die Coriolis-Kraft. Die BGL für ϕ
ist äquivalent zu
d
(mρ2 ϕ̇) = 0
dt
2
~ = ρ~eρ × m~e˙ρ =
d.h. mρ ϕ̇ ist ein Integral der Bewegung. Der Vergleich mit L
2
ρ ϕ̇~ez zeigt, dass die erhaltene Grösse der Betrag des Drehimpulses ist. Diese
Lösung für die zweite BGL hat eine einfache geometrische Deutung. Der Ausdruck 1/2ρ2 dϕ stellt die Fläche des Sektors dar, der von zwei unendlich dicht
benachbarten Radiusvektoren und dem dazwischenliegenden Bahnelement
gebildet wird. Wir bezeichnen diese Fläche mit df und schreiben den Drehimpuls der Masse als 2mf˙. Die Ableitung von f – die Flächengeschwindigkeit–
ist eine Konstante: In gleichen Zeitintervallen überstreicht der Ortsvektor
die gleiche Fläche (Flächensatz, 2. Satz von Kepler). Aus dieser Gleichung
können wir darüberhinaus ϕ2 berechnen: somit ist es möglich, diese Variable
in der Radialgleichung mit einem Parameter L zu ersetzen (”zu eliminieren”).
Somit lautet die Radialgleichung
mρ̈ =
L2
+ m · Kρ (ρ)
mρ3
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
50
~ konnten wir das Problem der Bewegung
Mit der Hilfe der Erhaltungsgrösse L
in einem zentralsymmetrischen Feld zu einer eindimensionalen Gleichung
für die einzige Variable ρ reduzieren! (1-dimensionale Probleme sind exakt
lösbar!!).
Wir wollen jetzt soweit wie möglich die radiale BGL integrieren. Wegen
L2
d[L2 /2mρ2 + U(ρ)] . dUef f
′
mρ̈ =
− U (ρ) = −
=−
mρ3
dρ
dρ
entwickelt sich die radiale Bewegung als würde sich die Masse m in einem
effektiven radialen Kraftfeld befinden. Dieses Kraftfeld besteht aus der Zentrifugalkraft und der Gravitationskraft und lässt sich schreiben als die radiale
Ableitung einer effektiven potentiellen Energie, die sich aus der Summe der
Zentrifugal-Energie und der potentiellen Energie der Gravitation zusammensetzt. Daraus folgt
Abbildung 4.3: Uef f als Funktion von ρ
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
51
1 2
.
mρ̇ + Uef f (ρ) = E
2
ein weiteres Integral der Bewegung, die totale Energie und die DGL
s
ρ̇ = ±
2
(E − Uef f (ρ))
m
Diese DGL kann sofort integriert werden, und zwar nach der Methode, die
wir für eindimensionale Probleme eingeführt haben:
t(ρ) = t(ρ0 ) ±
Z
dρ′
ρ
ρ0
q
2
(E
m
− Uef f (ρ))
Falls die effektive potentielle Energien Uef f (ρ) ein lokales Minimum besitzt
(siehe Abbildung), eröffnet sich die Möglichkeit von gebundenen Bahnen.
Diese sind dadurch charakterisiert, dass die Teilchenbahn innerhalb eines endlichen Kreisrings verläuft. Die Diskussion der Bahnen basiert auf die Lösungen der Gleichung E − Uef f (ρ) = 0. An diesen kritischen Radien ist die radiale Geschwindigkeit genau 0. Das bedeutet nicht, dass die Masse m anhält,
da die Drehgeschwindigkeit, gegeben durch L/(mρ2 ), endlich bleibt. Diese
Punkte sind Wendepunkte der Bahn, wo ρ aufhört zu wachsen und beginnt
kleiner zu werden. Man kann, je nach Wert von E, mindestens zwei Klassen
von Bahnen unterscheiden. Wenn E > Uef f (∞) ist, dann existiert nur eine
Lösung der Gleichung. ρmin ist dann ein minimaler Radius, den die Bahn
annehmen kann. Es existiert kein maximaler Radius – die Masse kommt aus
weiter Entfernung, kehrt bei ρmin um und verschwindet wieder ins Nichts:
die Bewegung des Teilchens ist infinit. Diesen Bahnen folgen zum Beispiel
die Kometen. Ist E > Uef f (∞) dann existiert ein minimaler (ρmin ) und ein
maximaler (ρmax ) Radius: Die Bahn ist finit und verläuft vollständig in einem
ringförmigen Gebiet. Das bedeutet aber nicht, dass die Bahn geschlossen ist
(geschlossen bedeutet, dass die Bahn nach bestimmten Zeiten immer wieder
an denselben Ort zurückkehrt). In der Tat werden geschlossene Bahnen dann
und nur dann beobachtet, wenn U(ρ) = − αρ (Kepler Problem!) oder ∝ ρ2 ist.
Bei beliebigen ρ-Abhängigkeiten sind geschlossene Bahnen äusserst selten;
stattdessen hat man sog. Rosettenbahnen. Die Zentrifugalbarriere (L 6= 0)
sorgt im Allgemeinen dafür, dass die Masse niemals zum Mittelpunkt des
Feldes gelangt, auch dann nicht, wenn das Feld anziehend ist.
4.3
Kepler-Problem
Wir kommen jetzt zur Begründung der Keplerschen Planetengesetze. Wir
betrachten die Sonne als Zentrum eines zentralgerichteten Gravitationsfeldes.
52
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
Abbildung 4.4: Rosettenbahn
−γm·M .
Eine Masse in diesem Gravitationsfeld hat die potentielle Energie
=
ρ
α
− ρ (M : Masse der Sonne, γ : Gravitationskonstante). Um etwas über die
Geometrie der Bahnen zu sagen, lösen wir die DGL
mit Lösung
ϕ̇
1
dϕ
= = ±L q
dρ
ρ̇
ρ2 2m(E − (− αρ +
ϕ(ρ) = ϕ(ρ0 ) ± L
Z
dρ′
ρ
ρ0
L2
))
2mρ2
q
ρ2 2m(E − (− αρ +
L2
))
2mρ2
.
Diese Gleichung enthält ein elementares Integral, mit Stammfunktion (u = ρ1 )
−
1
arctan
L
u − αm
L2
q
2Em
+ 2αm
u
L2
L2
− u2
= −
√
u−αm/L2
1
2Em/L2 +α2 m2 /L4
arctan
2
L
1 − [ √ u−αm/L
]2
2
2 2
4
2Em/L +α m /L
1
u − αm/L2
q
= − arccos
L
2Em/L2 + α2 m2 /L4
Wir setzen allfällige Konstanten zu Null und gehen von u nach ρ zurück, so
erhalten wir die Bahngleichung
ρ=
L2 /(αm)
1 + cos ϕ ·
q
2EL2 /(α2 m) + 1
Geometrisch gesehen ist diese Gleichung die Polarkoordinatendarstellung von
Kegelschnitten. Es ergibt sich die folgende Klassifizierung der Bahnen:
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
• für E =
•
−mα2
2L2
−mα2
2L2
53
= Uef f,min sind die Bahnen Kreise mit Radius L2 /(αm)
< E < 0 sind die Bahnen Ellipsen
• für E = 0 sind die Bahnen Parabeln
• für E > 0 sind die Bahnen Hyperbeln
Abbildung 4.5: Mögliche Bahnen im Gravitationsfeld
Somit ist das erste Keplersche Gesetz bewiesen: ” Die Planeten bewegen sich
auf Ellipsen, in deren einem Brennpunkt die Sonne steht”. Die weitere Untersuchung der obigen Resultaten zeigt, dass die grosse
q Halbachse a und die
a
kleine Halbachse b der Ellipse −α
respektiv
b
=
L
betragen. Für die
2E
mα
L
Fläche F der Ellipse gilt F = πab. Andererseits integrieren von dF
= 2m
dt
L
ergibt F = 2m
T , mit T die volle Umlaufzeit. Vergleich der beiden Ausdrücke
für F ergibt
2π
a3/2
T =q
γ · M
Für zwei verschiedene Ellipsenbahnen im gleichen Gravitationsfeld, die auch
zu zwei verschiedenen Massen gehören dürfen, erhalten wir
(
a1
T1 2
) = ( )3
T2
a2
In Worten: Drittes Keplersches Gesetz: Die Quadrate der Umlaufzeiten verhalten sich wie die dritten Potenzen der grossen Halbachsen.
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
4.4
54
Rutherfordsche Streuformel
Wir wollen uns jetzt mit den ungebundenen Bahnen in einer potentiellen
beschäftigen. Diese sind nicht nur für die HimEnergie der Form U(r) = −α
|~
r|
melsmechanik von Bedeutung, sondern auch für die Streuung von geladenen
Teilchen – zum Beispiel positive geladene Helium-Kerne, auch α-Teilchen genannt, an Atomkernen (die Elektronenhülle spielt dabei wegen der geringen
Elektronenmasse nur eine geringe Rolle). Diese Streuung wurde von Rutherford benutzt, um die Punktteilchen-Natur der Kerne zu beweisen. Wechselwirken zwei geladene Teilchen mit Ladung q1 und q2 , so ist die Konstante
1 q2
α = −q
, nach dem bekannten Coulomb-Gesetz. Schiesst man einen Strahl
4πǫ0
gleich schneller, parallel laufender Alphateilchen auf ein Target (bestehend
aus Atomen), so werden diese von den Kernen der Atome des Targets abgelenkt, siehe Abbildung. Wir wollen diese Ablenkung quantitativ untersuchen.
Für das hier betrachtete Potential verschwindet die Kraft im Unendlichen,
daher gehen die ungebundenen Bahnen im grossen Abstand vom Streuzentrum asymptotisch in Geraden über. Läuft ein Massenpunkt von r = −∞ auf
das Streu-Zentrum zu, so ändert sich sein Polarwinkel ϕ bis zum Erreichen
des minimalen Abstands rmin um (siehe Abbildung)
Z ∞
Ldr
q
∆ϕ =
rmin r 2 2m(E − V (r) − L2 )
2mr 2
Da der Lösungszweig r(ϕ) für r → ∞ aus dem vorher durchlaufenen durch
Spiegelung hervorgeht, erfährt der Polarwinkel nochmals dieselbe Verschiebung △ϕ. Beim Streuproblem erweist sich als zweckmässig, den Vorgang
mit den Parametern v∞ und s zu beschreiben, statt E und L. v∞ ist die
Geschwindigkeit im Unendlichen, s ist der senkrechte Abstand der Asymptoten vom Kraftzentrum - der Stossparameter –. Diese Umparametrisierung
erfolgt dank den Gleichungen
m 2
v
E =
2 ∞
L = limr→−∞ | ~r × m~r˙ |= limr→−∞ mr ṙ sin ϕ = mv∞ s
Somit ist
∆ϕ =
Z
sdr
∞
rmin
r
r2 1 −
s2
r2
−
2U (r)
2
mv∞
Darüberhinaus sind wir nicht an ∆ϕ sondern an den Streuwinkel χ interessiert, mit χ = π − 2△ϕ (siehe Abbildung):
Z ∞
χ
sdr
π
r
= −
2
2
2
rmin 2
r 1 − s − 2U (r)
r2
2
mv∞
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
55
Abbildung 4.6: Streuung in einem abstossenden (oben) und anziehenden (unten) Potential
rmin ist durch die Gleichung E − Uef f (r) = 0 definiert. Parametrisiert mit s
und v∞ ergibt diese Gleichung
rmin
v
u
u α2
α
= − 2 + t 2 4 + s2
mv∞
m v∞
Die Stammfunktion des zu berechnenden definiten Integrals ist
2
−s2 mv∞
+ αr
g(r) = arctan q
4 + 2αs2 mv 2 r − s2 m2 v 4
r 2 s2 m2 v∞
∞
∞
Da g(rmin ) = −π/2 (unabhängig vom Vorzeichen von α) und g(∞) =
arctan v2 αms erhalten wir schliesslich
∞
tan(χ/2) =
−α
2
s · m · v∞
Je nach Vorzeichen von α ist der Streuwinkel negativ (attraktive Potentiale
α > 0) oder positiv (repulsive Potentiale α < 0).
Um den Kontakt zu den experimentellen Bedingungen bei der Streuung
von Teilchen herzustellen, muss man berücksichtigen, dass die einfallenden
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
56
Teilchen in einem Strahl gebündelt sind. In der Regel ist der Strahl ”homogen”, d.h. vor der Streuung besitzen alle Teilchen nach Betrag und Richtung
dieselbe Geschwindigkeit und durch jedes senkrecht zur Teilchenzahl verlaufende Flächenelement △F laufen in der Zeit △t dieselbe Anzahl △N von
△N
Teilchen hindurch. Die Grössen I = △F
definiert den Fluss des Teilchen△T
strahls. In einem homogenen Strahl ist I vom Stossparameter s unhabängig,
d.h. in einem Streu-Experiment muss man damit rechnen, dass ein kontinuierlicher Bereich von Stossparametern gleichmässig im Teilchenstrahl vorkommt. Deswegen macht es keinen Sinn mehr von einem Stossparameter zu
sprechen, sondern man muss ein kleins Intervall [s, s+ds] definieren, innerhalb
welchem wir den Streuprozess analysieren. Als Wirkungsquerschnitt dσ für
Abbildung 4.7: Zur Definition des Stossparameters und des Wirkunsgquerschnitt
die Streuung in den Winkelbereich dχ um χ bezeichnen wir den Flächeninhalt
derjenige Ringfläche (siehe Abbildung) durch die alle in das Winkelintervall
[χ, χ + dχ] abgelenkten Teilchen hindurchtreten:
dσ = 2πs(χ, m, v∞ ) | ds |= 2πs(χ, m, v∞ ) |
∂s
dχ
∂χ
∂s
Je nachdem ob das Potential attraktiv oder repulsiv ist ∂χ
positiv oder negativ, aber wir definieren dσ als eine positive Fläche, und nehmen deswegen den
Absolut-Wert. Für die Streuung auf Raumwinkel dΩ = 2πsinχdχ bezogen,
der sich zwischen den in der Abbildung gezeichneten Kegeln mit Öffnung χ
KAPITEL 4. MECHANIK IM EUKLIDISCHEN RAUM
57
und χ + dχ erstreckt, erhalten wir den Zusammenhang
s(χ, m, v∞ ) | ∂s/∂χ |
dσ
=
dΩ
sin χ
dσ/dΩR wird differentieller Wirkungsquerschnitt bezeichnet. Das Integral
σtot = (dσ/dΩ′)dΩ′ heisst totalen Wirkungsquerschnitt. Zwischen einfallen∆NΩ
den Fluss I und Streu-Intensität IΩ = △Ω△t
(△NΩ ist die Anzahl Teilchen,
die während der Zeit △t durch den Raumwinkel ∆Ω gestreut werden), existiert eine wichtige Beziehung. Sollte bei der Streuung kein Teilchen verloren
gehen, dann gilt die Gleichung
I∆σ∆t = ∆N = ∆NΩ = IΩ ∆Ω∆t
Daraus folgt der Zusammenhang
IΩ
dσ
=
dΩ
I
Durch Messung von IΩ /I als Funktion des Winkels χ kann man überprüfen,
ob das angenommen Potential gerechtfertigt war. Die bei der Streuung an eisin χ
nem Potential der Form −α
erwartete dσ lässt sich aus s(χ) = mvα2 · 1−cos
herr
χ
∞
leiten und ergibt die berühmte Rutherfordsche Streuformel, die auch quantenmechanisch gilt:
α 2
1
dσ
=
4
2
dΩ
2mv∞ sin (χ/2)
Rutherford hat durch den Vergleich zwischen der gestreuten Intensität und
diesem Wirkungsquerschnitt vorgeschlagen, dass das Innere des Atoms im
Wesentlichen leer ist und dass in dessen Zentrum ein geladener, punktförmiger Kern sitzt, der ein Coulomb-Feld erzeugt.
Kapitel 5
Elektrostatik
Bis jetzt haben wir jedem physikalischen Objekt eine Masse zugeordnet: das
war das einzige physikalische Merkmal. Physikalische Objekte können aber
auch geladen sein. Die Ladung ist der zentrale Begriff in der Elektrostatik
und Magnetostatik. Es gibt zwei Arten von Ladungen, positive bzw. negative.
Einfache Experimente belegen, dass sich gleichnamige Ladungen abstossen,
während sich verschiedenartige Ladungen anziehen. Ein Beispiel von negativ
geladenen Massenpunkten ist ein Elektron. Positiv geladene Teilchen sind
zum Beispiel die Protonen, die zusammen mit den Elektronen die Bausteine
der ganzen Materie sind. Die Ladung, die ein Elektron oder ein Proton trägt,
beträgt 1.6 · 10−19C (C: Coulomb). Ferner stellt man fest, dass die Kraft zwischen zwei Ladungen q1 und q2 proportional zu ihrem Produkt ist und mit
dem Quadrat des Abstandes der beiden Ladungen abnimmt. Diese zusätzliche Kraft der Natur, die zwischen Ladungen existiert, ist die Coulomb Kraft.
Die Coulomb Kraft ist demnach der Gravitationskraft sehr ähnlich, mit dem
entscheidenden Unterschied, dass sie sowohl anziehend als auch abstossend
sein kann. Für die Coulomb-Kraft der Ladung q ′ auf die Ladung q gilt
~ q′ →q (~r′ , ~r) =
K
1
q ′ · q ~r − r~′
4πε0 |~r − r~′ |2 |~r − r~′ |
Nm2
1
= 9 × 109 2 , [q] = C
4πε0
C
Eine der Eigenschaften der Coulomb Kraft, die wesentlich zur Vielfalt beiträgt, die wir in der Natur beobachten, ist ihr vektorieller Charakter. Aber
genau diese Eigenschaft macht den Zugang zum Elektromagnetismus so kompliziert. In der Tat kann man oft in der Mechanik die Probleme durch Massenpunkte modellieren, die eben in einem Punkt lokalisiert waren. Der vektorielle Charakter der Gravitation äusserte sich als kugelsymmetrisches Kraftfeld,
58
59
KAPITEL 5. ELEKTROSTATIK
dV ′
ρ(r′ )
~r − ~r′
~r′
~r
Abbildung 5.1: Figur zur Coulomb-Gesetz und zum Superpositionsprinzip
das von diesem Massenpunkt produziert wird. Diese Kugelsymmetrie vereinfacht das Verständnis erheblich. Ladungen dagegen lassen sich auf einfache
Weise in beliebige Geometrien makroskopisch aufstellen und die eigentliche
Geometrie spielt bei vielen Anwendungen (siehe z.B. das Elektronenmikroskop oder die Antenne) eine sehr grosse Rolle: eine Ladung q, welche sich
in der Nähe einer makroskopischen Ladungsverteilung aufhält, spürt – nach
dem Superpositionsprinzip – die vektorielle Summe einer grossen Anzahl
Kräfte, die aus den einzelnen Ladungen entstehen: Bei der Anwesenheit von
N Ladungen q1 , ..., qN , wirkt auf die Ladung q die folgende Kraft:
~ ~r =
K
N
X
qi · (~r − ~ri )
q
·
4πε0 i=1 | ~r − ~ri |3
Haben wir eine kontinuierliche Ladungsverteilung vorliegen, die im Volumen
V eingeschlossen ist, so müssen wir von der Summation über die Punktladungen zu einer Integration über die räumliche Verteilung übergehen. Wir
setzen an die Stelle der Punktladung qi das Ladungselement ρ(~r′ )dV ′ , mit
dV ′ = dx′ dy ′dz ′ und ρ(~r′ ) die Ladungsdichte am Ort ~r′ . Somit ergibt sich
~ r) =
K(~
q
·
4πε0
Z
V′
ρ(~r′ )
~r − ~r′
dV ′
| ~r − ~r′ |3
Entsprechend kompliziert wird die Bewegung der Ladung q sein.
Bei diesen Ausfhrungen haben wir stillschweigend angenommen, dass die Anwesenheit von q die Ladungsverteilung ρ(~r′ ) nicht beeinflusst. Dann lässt sich
~ r ) schreiben. E
~ ist das elektrische Feld der Ladunsgverteidie Kraft als q · E(~
lung ρ(~r′ ), und ist durch die formelle Gleichung
.
~ r) =
E(~
1
·
4πε0
Z
V
ρ(~r′ )
~r − ~r′
dV ′
| ~r − ~r′ |3
gegeben. Somit wird jedem Raumpunkt ein (vektorielles) Feld zugeordnet,
das an verschiedenen Punkten im Raum verschiedene Werte und Richtungen
KAPITEL 5. ELEKTROSTATIK
60
annimmt. Wenn wir die Bestandteile der Ladungsverteilung festhalten, so ist
das Feld zeitunabhängig: es handelt sich um ein elektrostatisches Feld. Ist
~ r ) bekannt, lassen sich die Bewegungsgleichungen von q formulieren, in der
E(~
Form der Newton BGL. Hinter der Annahme eines elektrostatischen Kraftfeldes steckt eine Vereinfachung: es wird angenommen, dass q selbst keine
Kraft auf die Bestandteile der Ladungsverteilung ausübt. Diese Kraft führt,
genau betrachtet, möglicherweise zu einer zeitabhängigen Umverteilung der
Ladungen, die berücksichtigt werden sollte, um die genaue Bewegung von q
zu finden. Das Kraftfeld-Konzept der Elektrostatik ist deswegen eine Vereinfachung der Realität, die nur dann gut ist, wenn q eine ’kleine Störung’ ist.
Eine Ladung q, welche die Ladungsverteilung nicht beeinflusst, nennt man
~ ist eine Charakteristik der La”Probeladung”, und das elektrische Feld E
dungsverteilung und ist von q unabhängig.
Zusammenfassend, im Gegensatz zur Mechanik, dürfen wir nicht mehr
die räumliche Ausdehnung der Ladung gegenüber den in unserem Problem relevanten Abständen vernachlässigen. Diese Komplikation erfordert
die Einführung zusätzlicher mathematischer Begriffe aus der Vektoranalysis. Noch eine Bemerkung über das Wort ”klassisch”, das im Titel dieser
Vorlesung vorkommt. In vielen Fällen lässt sich die Bewegung einer Ladung
sehr gut durch die klassische Bewegungsgleichung der Mechanik beschreiben:
die Quantenmechanik – genauer gesagt: die Quantenelektrodynamik – liefert
im Allgemeinen kleine Korrekturen. Die klassische Elektrodynamik ist deswegen immer noch ein aktuelles Gebiet der Physik. Hinzu kommt, dass die
Beschreibung der elektrischen und magnetischen Felder durch die Maxwell
Gleichungen immer noch exakt ist.
Der Gradient
Der Begriff des Feldes stellt ein fundamentales Konzept in der Physik dar. Man unterscheidet zwischen Skalarfeldern und Vektorfeldern. Ein Skalarfeld Φ(~r) = Φ(x, y, z) ist
eine skalarwertige Funktion dreier unabhängiger Variablen, wobei sich die Zahl drei auf
die Dimension unseres Raumes bezieht.
p
Beispiel: Wir betrachten die Funktion Φ(~r) = α/( x2 + y 2 + z 2 ). Graphisch stellt man
solche Felder durch 2-dimensionale Schnitte dar, in denen die Flächen Φ(~r) = Konst
(Äquipotentialfläche) als Höhenlinien erscheinen. Der Abstand der Linien enstpricht dabei gleichen Wertunterschieden der Konstanten.
~ = K(~
~ r ) zu.
Ein Vektorfeld ordnet jedem Punkt im Raum eine vektorwertige Funktion K
Beispiel: Das Gravitationsfeld eines Masssenpunktes ist gegeben durch
~ r ) = −m 2 2~r 2 3/2 .
K(~
(x +y +z )
Graphisch lassen sich Vektorfelder mittels Feldlinien darstellen, wobei das Feld tangential
zur Feldlinie verläuft. Die Dichte der Feldlinien ist dann ein Mass für die Stärke des Feldes.
Für Skalarfelder kann man den Begriff der partiellen Ableitung einführen:
Φ(x + ∆x, y, z) − Φ(x, y, z)
∂Φ .
= lim
∆x→0
∂x
∆x
61
KAPITEL 5. ELEKTROSTATIK
Abbildung 5.2: Konstruktion zur Berechnung von dΦ (links) und graphische
Deutung des Gradienten (rechts)
(und ähnlich für y, z). Damit lässt sich die räumliche Änderung der Skalarfelder beschreiben. Wir betrachten zwei Punkte ~r1 und ~r2 , die durch eine kleine Strecke d~r voneinander
getrennt sind.
Die Änderung dΦ = Φ(~r2 ) − Φ(~r1 ) ist gegeben durch die folgende Summe:
dΦ
∂Φ
∂Φ
∂Φ
dx +
dy +
dz
∂x
∂y
∂z
∂Φ ∂Φ ∂Φ
= (
,
,
) · (dx, dy, dz)
∂x ∂y ∂z
. ~
= ∇Φ
· d~r
=
~ der Gradient von Φ und dΦ das totale Differential des Feldes Φ sind. Der
wobei ∇Φ
Gradient lässt sich deuten, indem man d~r in die Richtung wählt, so dass dΦ = 0 in
~ · dr~0 = 0 folgt, dass ∇Φ
~ senkrecht auf dr~0
dieser Richtung ist. Aus der Gleichung ∇Φ
~ senkrecht auf den
steht. Anderseits definiert dΦ = 0 Flächen Φ = Konst., so dass ∇Φ
Äquipotentialflächen steht. Sein Betrag ist ein Mass für die Stärke der Änderung von Φ,
wenn man senkrecht zu den Äquipotentialflächen fortschreitet.
Die Divergenz
Gegeben sei ein Vektorfeld ~a = ~a(~r ) . Die Operation div ~a erzeugt ein Skalarfeld
div ~a =
3
X
∂ai
~ · ~a
=∇
∂x
i
i=1
Rechnungsbeispiele:
1. Durch Anwendung der Produktregel folgt für ϕ(~r ) und ~a (~r ):
div (ϕ~a) =
3
3
3
X
X
∂
∂ϕ X ∂ai
ai
ϕ
ϕai =
+
∂xi
∂xi i=1 ∂xi
i=1
i=1
~ + ϕ∇
~ · ~a .
= ~a · grad ϕ + ϕ div ~a = ~a · ∇ϕ
2. Für ~a = const. folgt div ~a = 0. Ein konstantes Feld ist quellenfrei.
62
KAPITEL 5. ELEKTROSTATIK
3. Die Divergenz von ~r entspricht der Raumdimension,
div ~r =
3
X
∂xi
i=1
∂xi
=3
.
Ausgehend von
X
3
3
X
∂
∂2ϕ
∂
div grad ϕ =
ϕ =
≡ △ϕ
∂xi ∂xi
∂x2i
i=1
i=1
führen wir den Laplace-Operator ein:
△=
∂2
∂2
∂2
+
+
= div grad .
∂x21
∂x22
∂x23
Um der Divergenz eine physikalische Interpretation zu geben, definieren wir eine weitere Grösse der Vektoranalysis, den Fluss eines Vektorfeldes. Wir betrachten eine Fläche
S im Raum, in welchem das Vektorfeld ~a(~r) definiert ist. Auf der Fläche betrachten wir
~ Der Fluss von ~a durch die Fläche S ist definiert als
das Flächenelement dS.
Z Z
~
~a(~r) · dS
Φ=
S
In einem strömenden Gas mit der Dichte ρ(x, y, z) und mit einem Geschwindigkeitsfeld
~a
~
dS
Abbildung 5.3: Zur Definition des Flusses eines Vektorfeldes
~v (x, y, z) ist ΦS (~a = ρ · ~v ) die gesamte Anzahl Teilchen pro Zeiteinheit, die durch die
gesamte Fläche S hindurchströmt. Wir betrachten jetzt ein kleines Volumenelement dx ·
dy · dz = dV . und berechnen Φ(~a) durch die Wände von dV . Dazu werden wir die Summe
der Flüsse durch alle sechs Seitenflächen bilden. Betrachten wir zum Beispiel die mit ’1’
bezeichnete Fläche in der Figur. Aus dieser Fläche ist der Fluss Φ1 = −ax (1) · dy · dz. Da
wir mit einem infinitesimal kleinen Würfel zu tun haben, nehmen wir den Wert von ax im
Mittelpunkt der Fläche - wir nennen ihn den Punkt (1). In ähnlicher Weise schreiben wir
Φ2 = ax (2) · dy · dz. Nun sind im Allgemeinen ax (1) und ax (2) etwas verschieden. Da dx
klein genug ist, können wir schreiben ax (2) = ax (1) + ∂ax/∂x · dx. Somit beträgt der Fluss
durch die Flächen ’1’ und ’2’ [∂ax /∂x · dx · dy · dz]. Mit der selben Genauigkeit können wir
den Gesamtfluss durch alle 6 Flächen des Quaders berechnen:
Z Z
~ =∇
~ · ~a · dV
~a · dS
S(△V )
63
KAPITEL 5. ELEKTROSTATIK
Abbildung 5.4: Konstruktion zur Deutung der Divergenz eines Vektorfeldes
~a
Damit ist die Divergenz eines Vektorfeldes im Punkt ~r der Fluss – die nach aussen fliessende
Strömung- von ~a pro Volumeneinheit durch die Fläche eines infinitesimale Quaders um
~r. Diese physikalische Deutung lässt sich zu einem berühmten Satz der Vektoranalysis
verallgemeinern (Gauss’sche Satz):
Z Z Z
Z Z
~
~
dV ∇ · ~a =
~a · dS
V
S
Beweis: Man teile das Volumen V in infinitesimal kleine Quader, für welche dieR Beziehung
R
a·
zwischen Divergenz und Fluss gilt und summiere die linke und rechte Seite von
S(△Vi ) ~
~
~
dS = ∇ · ~a(~ri ) · dVi über die kleine Quader mit Index i. Der Beitrag der gemeinsamen
Seitenflächen zu den Flächenintegralen auf der linken Seite der Gleichung hebt sich wegen
der entgegengesetzten Richtungen der entsprechenden Flächennormale aus. Es bleibt das
Oberflächenintegral über die Einhüllende des Gesamtvolumens.
Die Rotation
Gegeben sei ein Vektorfeld ~a = ~a(~r ), dann erzeugt
~e1
~e2
~ × ~a = ∂/∂x1 ∂/∂x2
rot ~a = ∇
a1
a2
~e3
∂/∂x3
a3
ein Vektorfeld. Unter Benutzung des antisymmetrischen Tensors εijk lautet die Komponentenschreibweise
rot ~a =
3
X
i,j,k=1
εijk
∂
aj ~ek
∂xi
Man achte hier auf die Reihenfolge der Indizes.
Rechnungsbeispiele:
.
64
KAPITEL 5. ELEKTROSTATIK
1. Die Rotation des Produktes aus einem Skalar- und Vektorfeld ergibt nach Anwendung der Produktregel:
X
∂
rot (ϕ~a) =
εijk
(ϕaj ) ~ek
∂xi
i,j,k
=
X
εijk
i,j,k
i,j,k
=
X
∂aj
∂ϕ
aj ~ek +
~ek
εijk ϕ
∂xi
∂xi
~ × ~a + ϕ∇
~ × ~a
grad ϕ × ~a + ϕ rot ~a = ∇ϕ
.
2.
rot [f (r)~r ] = (grad f ) × ~r + f rot ~r = 0 .
Der erste Summand verschwindet, da gradf und ~r parallel sind; der zweite Summand verschwindet wegen rot ~r = 0.
3. Gradientenfelder sind wirbelfrei:
rot grad ϕ = 0 .
Das überprüft man komponentenweise. Für die 1. Komponente erhalten wir z.B.
∂
∂
(rot grad ϕ)1 =
(grad ϕ)3 −
(grad ϕ)2
∂x2
∂x3
∂2ϕ
∂2ϕ
=
−
=0 .
∂x2 ∂x3
∂x3 ∂x2
4. Wirbelfelder sind quellenfrei:
div rot ~a = 0
.
Um die Rotation physikalisch zu deuten, berechnen wir das Linienintegral (die Zirkulation von ~a um den geschlossenen Weg Γ)
Z
ΣΓ = ~a(~r)d~l
Γ
um eine kleine quadratische Schleife um ~r. Ohne Beschränkung der Allgemeinheit betrachten wir jetzt eine Schleife Γ in der xy-Ebene. Nach der Figur ist
ΣΓ = ax (1)dx + ay (2)dy − ax (3)dx − ay (4)dy
Mit ax (3) = ax (1) + ∂ax /∂y · dy und ay (4) = ay (2) − ∂ay /∂x · dx finden wir
~ × ~a)z · dx · dy
ΣΓ = (∇
Diese Gleichung lässt sich zu einer beliebig orientierten Schleife verallgemeinern:
~ × ~a) · dS
~
ΣΓ = (∇
n
~
und bestimmt eine eindeutige Beziehung zwischen der Rotation eines Vektorfeldes und
ihrer Zirkulation (die Richtung der Normalen ist so zu wählen: man lege den Zeigefinger
der rechten Hand in Schleifenrichtung, dann zeigt der Daumen entlang der ’richtigen’
Normalen). Die Verallgemeinerung dieser Gleichung auf beliebigen Schleifen Γ heisst Satz
von Stokes:
I
Z
~
~ × ~a) · dS
~
~a · dl = (∇
Γ
S
Zum Beweis: man decke die Fläche S mit infinitesimal kleinen Schleifen.
65
KAPITEL 5. ELEKTROSTATIK
Abbildung 5.5: Zur Deutung der Rotation eines Vektorfeldes
5.1
Die Grundgleichungen der Elektrostatik
Gegeben sei eine vorgegebene kontinuierliche Ladungsverteilung ρ(~r), die in
einem bestimmten Gebiet fest angeordnet sind. Formell ist der aus dem Superpositionsprinzip hergeleitete Ausdruck für das elektrische Feld eine exakte und vollständige Lösung des Problems, das elektrische Feld aus einer
Ladungsverteilung zu berechnen. Es existieren aber äquivalente Formulierungen der Gesetze der Elektrostatik als partielle Differentialgleichungen, und
für einige Probleme ist die Lösung solcher Gleichungen angemessener als die
Berechnung des Integrals.
1. Gesetz der Elektrostatik
Theorem:
Aus
~ r) =
E(~
folgt die Integralform
1
·
4πε0
Z
V
~r − ~r′
dV ′
ρ(~r )
′
3
| ~r − ~r |
Z
~ r ) · dS
~= 1
E(~
ǫ0
S(V )
′
Z
V
ρ(~r)dV =
q
ǫ0
R
~ durch eine beliebige
mit q = V ρ(~r)dV In Worten: der Fluss von E
geschlossene Fläche ist proportional zur Gesamtladung innerhalb
dieser Fläche. Die äquivalente DG (Differentialform) lautet:
~ =
div E
ρ(~r)
ǫ0
66
KAPITEL 5. ELEKTROSTATIK
R
~
~ · dS
~ = R div EdV
Die DG erhalten wir aus der Integralform aus S(V ) E
V
(Satz von Gauss) durch Gleichsetzen der Integranden. Das 1. Gesetz der
Elektrostatik drückt die Tatsache aus, dass die Quellen des elektrischen Feldes die elektrische Ladungen sind. Da man explizit das Gauss Theorem für
die Durchführung des Beweises benutzt, nennt man sie auch Gauss-Gesetz.
Beweis der Integralform:
Für den Beweis brauchen wir folgende wichtige Identitäten: Es gilt
~r − ~r′
1
~r
= −∇
′
3
| ~r − ~r |
| ~r − ~r′ |
Diese Identität lässt sich komponentenweise durch direkte Durchführung der
partiellen Ableitungen beweisen. Das Symbol ∇r bedeutet, dass die partiellen
Ableitungen nach der Variablen ~r durchgeführt werden. Darüberhinaus gilt
△
1
=0
| ~r − ~r′ |
falls ~r 6= ~r′ . Auch diese Gleichung lässt sich durch direkte Durchführung der
partiellen Ableitungen beweisen. Es folgt:
Z
S(V )
Z
Z
~r − ~r′
1
′
′
~
·
dV ρ(~r ) dS
4πε0 V ′
| ~r − ~r′ |3
S
Z
Z
1
1
~∇
~r
·
dV ′ ρ(~r′ ) dS
= −
4πε0 V ′
| ~r − ~r′ |
S
Z
Z
1
1
= −
·
dV ′ ρ(~r′ ) dV △r
4πε0 V ′
| ~r − ~r′ |
V
~ · dS
~ =
E
S ist irgendeine, die Ladungsverteilung umgebenden geschlossene Fläche.
Diese ”fiktive” Fläche wollen wir Gauss-Fläche nennen, da wir für ihre Herleitung den Gausschen Satz benutzt haben. V ist das von S eingeschlossenen
Volumen. Für die Berechnung des Integrals über die Variable ~r ∈ V von
1
△r |~r−~
setzen wir o.B.d.A ~r′ = 0 und schneiden wir eine kugelförmige Kar′ |
vität K um den Nullpunkt, so dass
Z
V
Z
Z
1
1
1
=
+
dV △
dV △
dV △
| ~r |
| ~r |
| ~r |
(V −K)
K
Das Integral über (V − K) ist Null, weil darin der Integrand indentisch Null
ist. Im Ursprung divergiert der Integrand: Das Integral über K berechnen
wir deshalb durch seine Transformation in ein Integral über die kugelfläche
∂K (Gausssche Satz). Es folgt:
Z
V
△
1
dV
| ~r |
=
Z
V
~ ·∇
~ 1 dV
∇
| ~r |
67
KAPITEL 5. ELEKTROSTATIK
Z
~
~ 1 dS
∇
| ~r |
∂K
= −4π
=
Zusammensetzung der Integrale ergibt die behauptete Integralform.
2. Gesetz der Elektrostatik
Um das zweite Gesetz zu formulieren, merken wir dass
Z
1
~r − ~r′
′
~
dV = −∇r
dV ′
ρ(~r′ )
ρ(~r )
′
3
′
′
′
| ~r − ~r |
| ~r − ~r |
V
V
Z
′
~ r ) kann als Gradient eines Potentials Φ(~r) geschrieben werde, mit
ist, d.h. E(~
1
Φ(~r) =
4πε0
Z
V′
ρ(~r′ )
dV ′
′
| ~r − ~r |
Diese Tatsache drückt man in der DG
~ r) = 0
rotE(~
aus, welche besagt, dass ein Gradientenfeld rotationsfrei ist. Die Integralform
~ entlang
folgt aus dem Satz von Stokes und besagt, dass die Zirkulation von E
~
~
eines geschlossenen Weg genau 0 sein muss. Aus E = −∇Φ(~r) folgt, dass das
~ wegunabhängig ist und
Linienintegral über E
Φ(~r) − Φ(~r0 ) = −
Z
~
r
~
r0
~ r ′ ) · d~r′
E(~
beträgt. Man bezeichnet diese Potentialdifferenz als Spannung U(~r,~r0 ). Die
Einheiten von U und von Φ sind das Volt (V ). Die zwei Gesetze der Elektrostatik können als Poissongleichung kombiniert werden. Die Poisson Gleichung
erhält man aus
~ · ∇Φ
~
−∇
=
ρ
ǫ0
△Φ(~r) = −
ρ(~r)
ǫ0
oder bei expliziten Berechnung von ∆Φ aus dem Integralausdruck für Φ .
Die Poisson Gleichung stellt eine partielle Differentialgleichung für die zweite räumliche Ableitung des elektrischen Potentials dar. Wie alle DG, hat
diese DG nur im Zusammenhang mit vorgegebenen Randbedingungen - Φ
68
KAPITEL 5. ELEKTROSTATIK
muss auf einer Fläche bekannt sein - eine Bedeutung. Die Poisson Gleichung
ist Gegenstand beträchtlicher mathematischer und numerischer Studien (sog.
Randwertprobleme der Elektrostatik). Die Poisson DG wird zum Beispiel in der Entwicklung sog. elektronenoptischer Systeme angewandt, die
zum Beispiel für die Fokussierung von Elektronen entwickelt werden (Elektronenmikroskop). Zusammenfassung: Es gibt zwei Gesetze, die das elektrostatische Feld vollständig bestimmen. Sie besitzen Integral und DG
Darstellungen. Aus diesen zwei Gesetzen werden alle Vorhersagen der Elektrostatik hergeleitet. Das Gausssche Gesetz allein kann kein Problem lösen,
weil das andere Gesetz berücksichtigt werden muss. Daher müssen wir noch
etwas anderes hinzufügen, wenn wir das Gausssche Gesetz zur Lösung eines
bestimmten Problems verwenden wollen. Zum Beispiel, müssen wir uns zuerst eine Vorstellung von der Form des elektrischen Feldes machen – wobei
wir von Symmetrieerwägungen ausgehen werden. Oder aber wir müssen irgendwie die spezifische Idee einführen, dass die Feldstärke der Gradient eines
Potentials ist uns somit das elektrische Feld wirbelfrei ist. Eine alternative
Formulierung ist die Poisson Gleichung.
5.2
Das elektrische Feld von einfachen Ladungsverteilungen
a: Feld einer Punktladung q
O.E.dA. sei die Punktladung am Ort (0, 0, 0). Das E-Feld kann nur eine
radiale Komponente haben. Deswegen
Z Z
~ · d~s
E
4πr 2 · Er (r)! =
=
⇐⇒ Er (r) =
q
q
ǫ0
4πǫ0 · r 2
und
φ(r) − φ(∞)(= 0) = −
Z
r
∞
Er (r)dr =
q
4πǫ0 · r
b: Feld einer geladenen Kugel
Eines der schwierigen Probleme, auf die Newton stiess, als er die Gravitation
untersuchte, bestand darin zu beweisen, dass eine feste Kugel von Materie
mit endlichem Radius R das selbe Gravitationsfeld besitzt wie ein Massenpunkt gleicher Masse im Zentrum der Kugel. Newton hat seine Theorie der
69
KAPITEL 5. ELEKTROSTATIK
Gravitation jahrelang nicht veröffentlicht, weil er nicht sicher war, ob dieses
Theorem richtig ist.
Durch die Integralform des Gaussschen Gesetzes lässt sich dieses Theorem
~ radial gesofort beweisen. Da es keine ausgezeichnete Richtung gibt, ist E
richtet. Wir konstruieren eine fiktive Kugelfläche S mit Radius r > R, die
konzentrisch zur festen Kugel verläuft. Die zu berechnende Feldstärke E(r)
kommt als Unbekannte im Gaussschen Gesetz vor:
Z
S
E(r)r 2sinϑdϑdϕ = Q/ε0
wobei Q die Gesamtladung der Kugel ist. Die Lösung dieser Gleichung ist
E(r) = 4πεQ0 r2 , r ≥ R. Das Potential am Ort ~r hängt nur von r ab, d.h. die
Äquipotentialflächen sind konzentrische Kugelflächen. Für r ≥ R kann Φ(r)
aus der Gleichung
Φ(r) − Φ(∞) = −
Z
r
r=∞
dr
Q
4πε0r 2
zu Φ(r) = 4πǫQ0 r bestimmt werden.
Als Übung: Berechne das Feld einer geladenen Kugelschale. Die
homogene Ladungsdichte ρ sei auf einer kugelförmigen Schicht der
Dicke δ beim Radius R verteilt.
c: Feld einer geladenen ebenen Schicht
Wir betrachten eine dünne Platte in der x − y-Ebene, auf welcher die homogene Flächenladungsdichte σ (die totale Ladung Q auf der Fläche A dividiert
~
durch A) aufgebracht wurde. Die Symmetrie des Problems suggeriert, dass E
orthogonal zur Platte steht. Darüberhinaus vermuten wir, dass aufgrund der
~ = E(z)
~
Translationssymmetrie in der x − y Ebene E
ist. Die Feldstärke muss
(ihrem Betrag nach) auf beiden Seiten gleich sein. Wir wählen als Gausssche
Fläche eine rechteckige Schachtel, welche die Schicht schneidet, siehe Figur.
Die beiden Seitenflächen parallel zur Schicht haben den gleichen Flächeninhalt A. Das Feld ist normal zu diesen beiden Flächen und parallel zu den
anderen vier. Der Gesamtfluss ist die Unbekannte | E(z) | ·2A (der Beitrag
von den anderen vier Flächen ist Null). Die Gesamtladung im Innern der
Schachtel ist σ · A. Wegen dem Gauss Gesetz ist deshalb | E(z) |= σ/2ε0 ,
unabhängig von | z |. Die Äquipotentialflächen verlaufen parallel zur x − y
Ebene, und es gilt
Φ(z) − Φ(0) = −
Z
0
|z|
σ
−|z|σ
=
2ǫ0
2ǫ0
70
KAPITEL 5. ELEKTROSTATIK
~
E
A
Abbildung 5.6: Feld einer geladener Ebene
d: Randbedingungen an Grenzflächen
~ an einerbeliebigenGrenzAls Nächstes untersuchen wir das Verhalten von E
fläche S, welche die Flächeladungdichte σ(~y ) trägt. Wir legen zuerst um die
Fläche S ein GaussschesKästchen mit dem Volumen △V . Die Kante senkrecht zu S habe die Länge △x, die wir als sehr klein wählen. Somit kann
der Fluss durch die Seitenkanten des Kästchens vernachlässigt werden. Das
~ a · ~n und E
~ i · ~n (~n senkrecht zu S). Das
Problem hat somit zwei Ukebannte: E
1. Gesetz liefert eine Gleichung zwischen diesen zwei unbekannten:
~a − E
~ i) = σ
~n · (E
ǫ0
Die Normalkomponente des elektrischen Feldes verhält sich an der Grenzfläche unstetig, der Sprung beträgt ǫσ0 . Um das Verhalten der Tangential~ zu untersuchen, ziehen wir eine Stoksche-Kontur Γ um
komponente von E
die Fläche S, dessen Dicke so gering ist, dass das Linienintegral entlang der
Kanten vernachlässigbar ist. ~t ist tangential zu S und definiert die Normale zur Fläche, die vom Kontour Γ definiert ist. Anwendung des Stokeschen
71
KAPITEL 5. ELEKTROSTATIK
Gesetzes liefert die Gleichung
~a − E
~ i)
(~t × ~n) · (E
= 0, ∀~t
⇐⇒
~a − E
~ i) = 0
~n × (E
Diese Gleichung drückt die Stetigkeit der Tangentialkomponente aus: Die
~
Tangentialkomponente des E-Feldes
ändert sich nicht beim Durchgang durch
eine geladene Grenzfläche.
e: Der Plattenkondensator
Unter einem Plattenkondensator versteht man ein System von zwei parallel
zueinander angeordneten Platten mit dem Abstand d und der Fläche F . Die
beiden Platten tragen homogen verteilt die entgegengesetzten Ladungen ±Q,
mit der positiven Platte bei −d/2 und die negative bei d/2. Die Flächenladungsdichte beträgt dann σ = Q/F . Zur Vereinfachung des Problems werden
die Streufelder am Rand vernachlässigt, d.h. es wird angenommen, dass die
Platten parallel zur x − y Ebene unendlich ausgedehnt sind (F >> d). Somit
ist das Feld im Inneren des Kondensators ǫσ0 , ausserhalb des Kondensators
ist das elektrische Feld genau 0, und zwar auch in unmittelbarer Nähe einer der Platten. Die Potentialdifferenz zwischen der positiv und der negativ
geledenen Platte (die Spannung) beträgt
U = Φ(−d/2) − Φ(d/2) = −
Z
−d/2
d/2
dz
σ
Q
σ
=d· =d
ǫ0
ǫ0
F · ǫ0
.
Wir definieren die Kapazität C eines Kondensators durch C = Q
. Diese
U
Grösse bestimmt die Ladung, die bei gegebener Spannung auf dem Kondensator passt. Für die Kapazität des Flächekondensators folgt
C=
F · ǫ0
d
C hängt somit im Allgemeinen von der Geometrie des Objektes ab, auf welchem wir eine Ladung anbringen. Je grösser die Kapazität ist, desto mehr
Ladung braucht man, um eine gegebene Spannung zu erzielen. Anders ausgedrückt: mit einer vorgegebenen Ladung lässt sich eine kleinere Spannung
erreichen je grösser die Kapazität ist. Aus der Definition von C sehen wir, dass
die Einheit der Kapazität C/V olt ist. Diese Einheit nennt man auch Farad.
Wir können mit dieser neuen Einheit, ǫ0 anders ausdrücken: ǫ0 = (36π·109 )−1
Farad/m. Das ist sogar die Einheit, die am häufigsten verwendet wird. Ein
72
KAPITEL 5. ELEKTROSTATIK
Plattenpaar mit einer Fläche von einem Quadratzentimeter und einem Abstand von 1 mm hat eine Kapazität von einem Pikofarad (10−12 ). Objekte
mit Kapazitäten ∼ 10−19 Farad sind Gegenstand der heutigen Forschung, die
mit ”Nanophysik” bezeichnet wird. Diese kleinsten Kapazitäten führen dazu,
dass das Anbringen eines einzelnen Elektrons auf solche Nano-Objekte eine
erhebliche Potentialerhöhung verursacht, so dass das Anbringen eines weiteren Elektrons praktisch blockiert ist: man spricht von ”Coulomb Blockade”.
Bemerkung: Wir haben bis jetzt von Spannung und Kapazität zwischen
zwei Ladungsträgern gesprochen. Allgemein spricht man auch von der Spannung und der Kapazität eines einzelnen Objekts. Man sagt, ein Linsenelement einer Elektronenkanone, eine Metallplatte oder eine Metallkugel seien
auf eine bestimmte Spannung gelegt. Dabei ist Folgendes gemeint. Man hat
die Ladung Q aus einem sehr grossen Objekt entfernt – die ”Erde” – deren
Kapazität so gross ist, dass man praktisch Ladung entfernen kann, ohne ihr
Potential zu verändern. Die Erde wird üblicherweise als ’unendlich’ entfernt
betrachtet und deshalb auf Potential 0 gesetzt. Die entfernte Ladung wird auf
ein massives Objekt gebracht: je nach Kapazität, nimmt dieses Objekt ein
bestimmtes Potential an. Dieses Potential ist die Spannung. Diese Spannung
entspricht der Arbeit, die geleistet werden muss, um eine Einheitsladung von
der Erde bis zum Objekt zu befördern. Wir wollen ein konkretes Beispiel eines
massiven Objekts betrachten, und zwar fragen wir uns, auf welchem Potential
ist eine geladene Kugelschale von Radius R. Das elektrischen Feld ausserhalb
der Kugelschale ist radialgerichtet und beträgt E = Q · (4πε0r 2 )−1 |~~rr| . Denken
wir uns eine - einfachheitshalber - kugelförmige ”Erdschale” unendlich weit
entfernt von unserer geladenen Kugelschale. Die Beförderung einer positive
Einheitsladung von dieser Erde zur Kugeloberfläche erfordert die Arbeit
Φ(R) − Φ(∞) = −
Z
R
∞
E(r)dr =
Q
4πǫ0 R
Die Oberfläche der Kugel ist daher auf einer Spannung 4πεQ0 R . Wie im Beispiel
der Kondensatoren, ist diese Spannung proportional zu der Ladung Q. Die
Kapazität ist 4πε0 R. Wie aus dieser Rechnung ersichtlich ist, skaliert die
Kapazität eines Objektes mit den linearen Dimensionen dieses Objektes, und
nicht mit dessen Fläche.
f: Selbstenergie einer kontinuirlichen Ladungsverteilung
1
U(ρ) =
2
Z
φ(~r) · ρ(~r)dV
73
KAPITEL 5. ELEKTROSTATIK
ist die Arbeit, die für das Erzeugen der (lokalisierten) Ladungsverteilung ρ
benötigt wurde. Dieser Ausdruck lässt sich mit P.I. umformen:
Z
V
ψ(~r)∂j χ(~r) =
Z
∂V
ψ(~r)χ(~r)nj d~s −
Z
V
χ(~r)∂j ψ(~r)
Wir erhalten:
ǫ0 Z
dV φ · △φ
2Z
ǫ0
~ · ∇φ
~
dV ∇φ
=
2 Z
ǫ0
~ 2 (~r)
dV E
=
2
U(ρ) = −
g: Gleichgewicht in einem elektrostatischen Feld: die
Stabilität der Atome
Wir stellen uns eine Punktladung im Feld von anderen Ladungen vor. Die
Bedingungen für ein mechanisches Gleichgewicht sind a) die Ladung ist an
einem Ort P mit Feld 0 und b) wenn das GG stabil sein soll, ist es notwendig,
dass es eine rücktreibende Kraft gibt, wenn wir die Ladung in irgendeine
Richtung von P wegbewegen. Mit anderen Worten: das elektrische Feld muss
an allen benachbarten Punkten nach innen gerichtet sein - auf den Punkt P
zu. Wir werden zeigen, dass dies eine Verletzung des Gauss’schen Gesetzes
ist, wenn in P keine Ladung vorhanden ist (ausser der Probeladung, die nicht
an der Bildung des Feldes beteiligt ist). Stellen wir uns eine Gauss Fläche
wie in der Figur vor. Da wir annehmen, dass das elektrische Feld in der
P
S
Abbildung 5.7: Feldverteilung für Gleichgewichtslage
Umgebung überall auf P gerichtet ist, ist der Fluss durch die Gauss Fläche
bestimmt nicht null. Aber da wir vorausgesetzt haben, dass in P keine Ladung
74
KAPITEL 5. ELEKTROSTATIK
ist, widerspricht eine solche Feldkonfiguration dem Gauss’schen Gesetz. Wir
haben oft gesagt, dass die Stabilität der Atome - und somit die der Materie
- aufgrund der Coulomb Kraft zwischen Elektronen und Protonen zustande
kommt. Diese Überlegungen zeigen uns, dass die Materie auf keinen Fall
das Resultat von Elektrostatik zwischen statischen Punktladungen ist. Die
Stabilität der Atome wird nur durch die quantenmechanische Behandlung
der Bewegung eines Elektrons im Coulomb Feld des Kerns erklärt.
h: Das Feld eines Dipols
Wir betrachten eine Ladung q am Ort d~ und eine Ladung −q im Nullpunkt.
~
Wir wollen das von diesem Ladungspaar verursachte E-Feld
berechnen, und
~
~
zwar im Limes d → 0 aber q · d → ~p. Eine solche Ladunsgverteilung bildet
einen Dipol und der Vektor ~p ist das elektrische Dipolmoment. Für das
elektrischen Potential eines Dipols finden wir:
q
1 −q
(
+
)
4πε0 | ~r | | ~r − d~ |
1 ~p · ~r
=
4πε0 | ~r |3
φ(~r) =
da
1
d~ · ~r
1
∼
)= q
= (1 + 2 )
r
| ~r − d~ |
r 2 + d2 − 2~r · d~ r
1
~ = −∇φ(~
~ r ) berechnen wir
Aus E
−1
~ 1 + 1 ∇(~
~ p · ~r))
(~p · ~r∇
4πε0
| ~r |3 | ~r |3
3[~
p · ~r]~r − p~ | ~r |2 =
| ~r |5
~ =
E
Am Ort des Dipols selbst ist der Ausdruck für das Potential divergent, und
~ aufpassen. Die folgende Überdeshalb müssen wir mit der Berechnung von E
~ korrigiert werden muss. Wir betrachten
legung zeigt, wie der Ausdruck von E
eine Kugel mit Radius R und setzen einen Dipol p~ in den Ursprung der Kugel. O.E.d.A wählen wir p~ = p(0, 0, 1). Benutzen wir den obigen Ausdruck
RRR
~
für die Berechnung von
Kugel EdV für das elektrischen Feld eines Diplos
dann erhalten wir (siehe Übungen)
Z Z Z
Kugel
~
EdV
= (0, 0, 0)
75
KAPITEL 5. ELEKTROSTATIK
Allerdings liefert ein P.I. (siehe übungen)
−
1
4πε0
Z Z Z
~ ~p · ~r dV
∇
r |3
Kugel | ~
= (0, 0, −
p
)
3ε0
Damit die beide Integrale identisch sind, muss der Ausdruck für das elektrische Feld eines Dipols modifiziert werden. Der exakte Ausdruck für das
elektrische Feld ist
~ r) =
E(~
1
1 3[~p · (~r)](~r) − p~ | ~r |2 4π
−
· δ(~r)~p
5
4πε0
| ~r |
4πε0 3
die sog. Delta-Funktion δ(~r) ist eine spezielle Funktion der mathematischen
R
Physik, die exakt 0 für ~r 6= 0 ist, ∞ für ~r = 0 ist, aber mit dV δ(~r) = 1.
Die hinzugefügte Delta-Funktion liefert nur am Ort des Dipols einen Feldbeitrag und errfüllt den Zweck, das geforderte Volumenintegral zu liefern. Die
Delta -Funktion liefert ausserhalb des Dipols keinen Beitrag. Der erste Term
beschreibt das elektrische Feld für ~r 6= 0. Graphisch sieht das elektrische
Dipolfeld etwa wie in der Figur aus.
q
E
r
p
Abbildung 5.8: Feld eines Dipols
5.3
Elektrostatik von Metallen
Ein elektrischer Leiter (ein Metall) ist ein fester Körper, der für die chemische
Bindung viele ’freie’ Elektronen benötigt. Die Elektronen können sich frei
bewegen in einem positiven Hintergrund von Ionen, welche fest am Gitter
gebunden sind. Man benutzt oft ein Jellium Modell, um freie Elektronen
in einem Metall zu beschreiben. Elektronen können sich frei in der Materie
bewegen, aber sie können die Oberfläche nicht verlassen: an der Oberfläche
existiert eine Barriere – die sog. Austrittsarbeit (etwa 4-5 eV) – die es den
76
KAPITEL 5. ELEKTROSTATIK
EPot
4-5 eV
x
Abbildung 5.9: Potentielle Energie eines Elektrons in einem Metall
Elektronen schwer macht, die Oberfläche zu verlassen. Die Komponenten
eines elektronenoptischen Ensembles, wie sie im Elektronenmikroskop oder
Elektronenspektrometer verwendet wird, besteht aus einem Metall. Es ist
deshalb wichtig zu lernen, was passiert wenn man Ladungen auf eine solche
Komponente aufbringt. Setzt man ins Innere eines Metalls eine Extraladung,
entsteht ein elektrisches Feld, welches die freie Elektronen in Bewegung setzt.
Entweder muss der auf diese Weise hervorgerufene Strom beständig von
äusseren Energiequellen in Gang gehalten werden, oder die Bewegung der
Elektronen lässt nach, wenn sich die Quellen entladen, die das anfängliche
Feld erzeugten. Bei ’elektrostatischen’ Situationen betrachten wir keine
stetigen Stromquellen (das tun wir später in der Magnetostatik): daher
bewegen sich die Elektronen nur so lange, bis sie sich so angeordnet haben,
dass sie überall im Innern des Leiters das elektrische Feld null erzeugen
(dies geschieht gewöhnlich in einem Bruchteil einer Sekunde.) Bliebe ein
Feld übrig, so würde dieses Feld noch weitere Elektronen in Bewegung
setzen; die einzige elektrostatische Lösung ist die, dass das Feld im Innern
überall Null ist. Somit ist der Gradient des Potentials Null. Das bedeutet,
dass sich V (x, y, z) von Punkt zu Punkt nicht ändert: Jeder Leiter ist ein
Äquipotentialbereich und seine Oberfläche ist eine Äquipotentialfläche.
Da das elektrische Feld in einer leitenden Substanz überall Null ist, ist
~ Null und nach dem Gauss’schen Gesetz muss die
die Divergenz von E
Ladungsdichte im Innern des Leiters ebenfalls Null sein. Wenn es in einem
Leiter keine Ladungen gibt, wie kann er dann geladen werden? Was meinen
wir damit, wenn wir sagen, ein Leiter sei ”geladen”? Wo sind die Ladungen?
Die Antwort ist, dass sie auf der Oberfläche des Leiters sitzen, wo es
starke Kräfte gibt, die sie zurückhalten - sie sind nicht völlig ”frei”. In der
Festkörperphysik lässt sich zeigen, dass die überschüssige Ladung jedes
Leiters im Mittel in einer oder zwei atomaren Schichten an der Oberfläche
sitzt.
Dieses Bild gilt auch, wenn wir eine bestimmte Anzahl Ladungen an einem
bestimmten Ort der Oberfläche anbringen. Diese lokale Ladung kann nicht
77
KAPITEL 5. ELEKTROSTATIK
so überleben: sofort verteilt sich die Ladung auf die gesamte Oberfläche,
und zwar mit den Bedingungen i) das Feld im Innern des Metalls ist genau
0 und ii) seine Tangentialkomponente ist auch 0. Wenn es dort eine solche
gäbe, würden sich die Elektronen entlang der Oberfläche bewegen; es gibt,
parallel zur Oberfläche, keine Kräfte, die das verhindern.
Mit Hilfe des Gauss’schen Gesetzes berechnet sich die Feldstärke unmittelbar
ausserhalb eines Leiters mit der lokalen Oberflächenladungsdichte σ zu σ/ε0 ,
und das Feld ist senkrecht zur Oberfläche (schliesslich ist die Oberfläche
eines Leiters eine Äquipotentialfläche).
Faraday Käfig
Betrachten wir jetzt unter dem gleichen Gesichtspunkt das Problem eines
hohlen Behälters - ein Leiter mit einem Hohlraum. Es gibt kein Feld in dem
Metall, aber wie steht es mit dem Hohlraum? Wir werden zeigen, dass keine
Felder existieren, wenn der Hohlraum leer ist - unabhängig davon, welche
Form der Leiter oder der Hohlraum hat (Faraday Käfig). Wir betrachten
+
+
+
+
+
+
+
+
+
-
-
++
-?
+
M
+
+
+
?+
+
+
+
+
+
+
+
+
S
+
+
+
+
+
Abbildung 5.10: Faraday Käfig
eine Gauss’sche Fläche wie S, die den Hohlraum umschliesst, aber überall
im Innern der leitenden Materie bleibt. Überall auf S ist das Feld Null; es
gibt daher keinen Fluss durch S und die Gesamtladung im Innern von S
ist Null. Aber im Allgemeinen können wir nur daraus schliessen, dass es auf
der inneren Oberfläche des Leiters gleiche Mengen positiver und negativer
Ladung gibt. Es könnte eine positive Oberflächenladung auf einem Teil und
eine negative auf einem anderen Teil geben, wie es in der Figur angezeigt
ist. Das Gauss’sche Gesetz schliesst das nicht aus. Was natürlich in Wirk-
KAPITEL 5. ELEKTROSTATIK
78
lichkeit geschieht, ist, dass die umgekehrt gleichen Ladungen auf der inneren
Oberfläche sich aufeinander zubewegen und dann vollständig kompensieren.
Wir können zeigen, dass sie sich vollständig kompensieren müssen, wenn wir
~ immer Null ist. Nehdas Gesetz verwenden, nach dem Zirkulation von E
men wir an, dass es Ladungen auf bestimmten Teilen der inneren Oberfläche
gäbe. Wir wissen, dass es dann an anderer Stelle eine gleiche Anzahl entge~ bei den
gengesetzter Ladungen geben muss. Nun müssten alle Linien von E
positiven Ladungen beginnen und an den negativen Ladungen enden (da wir
nur den Fall betrachten, in dem es keine freien Ladungen im Hohlraum gibt).
Stellen wir uns nun eine Schleife M vor, die durch den Hohlraum entlang einer Kraftlinie von einer positiven zu einer negativen Ladung führt und dann
über den Leiter zu ihrem Ausgangspunkt zurückkehrt. Das Integral entlang
einer solchen Kraftlinie von der positiven zur negativen Ladung wäre nicht
~ = 0. Wir erhielten daher
Null. Das Integral durch das Metall ist Null, da E
R
~ ~
~
M Edl 6= 0. Aber das Linienintegral von E um eine geschlossene Schleife
in einem elektrostatischen Feld muss immer Null sein. Daher kann es keine
Felder innerhalb des leeren Hohlraums geben und auch keine Ladungen auf
der inneren Oberfläche: das erklärt das Prinzip der Abschirmung durch einen
Metallkäfig.
Dieses Resultat kann für die Überprüfung des Gauss’schen Gesetzes – und
schlielich von der Genauigkeit der r −2 -Abhängigkeit des Coulomb’schen Gesetzes – benutzt werden. Man hat ein Elektrometer in das Innere einer grossen Kugel gesetzt und beobachtet, ob Ablenkungen auftreten, wenn die Kugel
auf Hochspannung gebracht wird. Man erhielt immer das Resultat null. Wenn
man die Geometrie des Apparates und die Empfindlichkeit des Instrumentes
kennt, ist es möglich, das kleinste nachweisbare Feld auszurechnen. Mit dieser Zahl kann man eine obere Grenze für die Abweichung des Exponenten
von zwei angeben. Wenn wir schreiben, dass die Coulomb Kraft ∝ r −(2+ε) ,
dann hat man festgestellt, dass ε < 10−9 ist.
Feld an einer Spitze
Wenn wir einen Leiter aufladen, der keine Kugel ist, sondern eine Spitze hat,
so ist das Feld in der Umgebung der Spitze viel stärker als in den anderen
Bereichen. Eine relativ kleine Ladungsmenge an der Spitze kann eine grosse
Flächendichte verursachen. Eine grosse Ladungsdichte bedeutet ein starkes
Feld in der unmittelbaren äusseren Umgebung. Quantitativ: wir legen zwischen Spite und Schirm (Feldemission-Mikroskop) eine Spannung U. Diese
Spannung bewirkt ein nahezu radialen elektrischen Feld E(r), dessen Betrag
79
KAPITEL 5. ELEKTROSTATIK
wir mit Hilfe des Gauss-Gesetz (Integralform) zu
E(r0 ) =
U
r0
bestimmen, wobei r0 den Krtümmungsradius der Spitze ist. Bei einem Wert
r0 = 1nm und U = 4V erreichen wir in der Nähe der Spitze eine sehr grosV
se Feldstärke von etwa 4 · 107 cm
. Nachteile: Wenn das elektrische Feld zu
stark ist, wird an einem Luftmolekül ein Elektron weggerissen und durch das
Feld beschleunigt. Wenn das Feld sehr stark ist, kann die Ladung, ehe sie
auf ein anderes Atom trifft, genügend beschleunigt werden, um ein Elektron
aus diesem Atom herauszuschlagen. Daraus resultiert, dass mehr und mehr
freie Ladungen erzeugt werden. Ihre Bewegung führt zu einer Entladung oder
einem Funken. Wenn man einen Körper auf hohes Potential laden will und
nicht möchte, dass er sich in Form von Funken in die Luft entlädt, so muss
die Oberfläche absolut glatt sein, damit es keine Stelle gibt, an der das Feld
abnormal stark ist. Die starken Felder an Spitzen haben aber auch interessant positive Entwicklungen erlaubt. Das Feldemissionenmikroskop von E.
Müller ist eine davon. Das Feldemissionsmikroskop ist folgendermassen gebaut: eine sehr feine Nadel, deren Spitze einen Durchmesser von ungefähr
1000 Angström hat (oder weniger!!) wird in die Mitte einer Glaskugel gebracht, deren Inneres luftleer gepumpt wird. Die innere Oberfläche der Kugel
wird mit einer dünnen leitenden Schicht eines fluoreszierenden Materials versehen und man legt eine Spannung zwischen der fluoreszierenden Schicht und
der Nadel an. Betrachten wir zunächst, was passiert wenn die Nadel relativ
zur fluoreszierenden Schicht negativ geladen ist. Die Feldlinien sind an der
scharfen Spitze sehr stark konzentriert. Die elektrische Feldstärke kann bis zu
40 Millionen Volt pro Zentimeter betragen. In so intensiven Feldern werden
Elektronen aus der Oberfläche der Nadel abgezogen und entlang der Potentialdifferenz zwischen der Nadel und der fluoreszierenden Schicht beschleunigt.
Wenn sie dort ankommen, bewirken sie, dass Licht emittiert wird, genau wie
in einer Fernsehbildröhre. Die Elektronen, die an einem vorgegebenen Punkt
auf der fluoreszierenden Fläche ankommen, sind in ausgezeichneter Näherung
diejenigen, die das andere Ende der radialen Feldlinie verlassen, denn die
Elektronen bewegen sich entlang der Feldlinie, die von der Spitze zur Oberfläche verläuft. Daher sehen wir auf der Oberfläche eine Art Abbildung der
Nadelspitze. Genauer gesagt sehen wir ein Bild des Emissionsvermögens der
Nadeloberfläche - es stellt die Leichtigkeit dar, mit der Elektronen die Oberfläche einer Metallspitze verlassen können. Wenn das Auflösungsvermögen
hoch genug wäre, könnte man hoffen, die Orte der einzelnen Atome auf der
Nadelspitze zu sehen. Bei Elektronen ist dieses Auflösungsvermögen nicht erreichbar. Erstens gibt es eine quantenmechanische Beugung der Elektrowel-
KAPITEL 5. ELEKTROSTATIK
80
le, die das Bild verwischt. Zweitens haben sie aufgrund ihrer Bewegung im
Innern des Metalls eine kleine seitwärts gerichtete Anfangsgeschwindigkeit,
wenn sie die Nadel verlassen. Diese zufällige Seitwärtskomponente trägt dazu
bei, dass das Bild verwischt wird. Das Zusammenwirken dieser beiden Effekte begrenzt das Auflösungsvermögen auf ungefähr 2.5 nm. Wenn wir jedoch
die Polarität umkehren und eine kleine Menge Heliumgas in die Glaskugel
bringen, so ist ein sehr viel grösseres Auflösungsvermögen möglich. Wenn
ein Heliumatom mit der Spitze der Nadel zusammenstösst, so entreisst das
dort herrschende intensive Feld dem Heliumatom ein Elektron, so dass das
Heliumatom positiv geladen übrigbleibt. Das Heliumion wird dann auswärts
entlang einer Feldlinie beschleunigt, die zu der fluoreszierenden Schicht führt.
Da das Heliumion viel schwerer als das Elektron ist, ist der Effekt der thermischen Geschwindigkeiten kleiner als im Fall des Elektrons. Anstelle eines
verwischten Bildes erhält man eine sehr viel deutlichere Abbildung des Punktes. Mit dem Feldemissionsmikroskop für positive Ionen war es möglich, eine
106 -fache Vergrösserung zu erreichen - und damit einzelne Atome zu sehen.
Die Figur ist ein Beispiel für die Resultate, die mit einem Feldemissionsmikroskop erzielt wurden. as Feldemissionsmikroskop hat es zum ersten Mal
möglich gemacht, dass Menschen Atome sehen konnten. Wenn man bedenkt,
wie einfach dieses Instrument ist, so ist das eine beachtliche Leistung.
Field Ion Microscope at Oak Ridge National laboratory, Tennessee (USA). In this field ion micrograph
of a nickel-molybdenum (Ni4Mo) intermetallic compound (left), each dot is a single atom. In this
computer reconstruction of the sharp end of a needlelike field ion specimen (center), concentric rings
appear because of the intersection of the atomic terraces with the surface of the specimen. Right: This
field evaporation sequence shows the gradual removal of eight of the last nine atoms on the central
atomic terrace of a nickel-zirconium (Ni7Zr2) intermetallic catalyst. One atom is evaporated from the
central terrace between each pair of frames.
KAPITEL 5. ELEKTROSTATIK
5.4
81
Elektrostatik eines Isolators (= Dielektrikum)
In der Natur treten nicht nur Metalle auf, sondern auch Isolatoren. In Metallen sind einige Elektronen (typischerweise 1 Elektron pro Baustein) im
Inneren frei beweglich. Isolatoren (sowohl als Festkörper als auch als Flüssigkeiten) sind Materialien, bei welchen alle Elektronen an Atome gebunden
sind. Damit ist gemeint, es gibt eine Energiebarriere, die überwunden werden muss, um Elektronen in Bewegung zu setzen. Diese Energiebarriere ist
eine Konsequenz der chemischen Bindung. Bringt man eine Ladung auf einen
Isolator, so bleibt diese Ladung an Ort und Stelle lokalisiert.
Wir wollen jetzt untersuchen, was in einem Isolator passiert, wenn man ein
elektrisches Feld einschaltet. Um das Problem zu vereinfachen, betrachten
wir ein Elektron, das gebunden um ein Proton ’herumkreist’. Wir vermuten
Folgendes: wenn sich ein Atom in einem elektrischen Feld befindet, dann zerrt
das Feld die Elektronen in eine Richtung und den Kern in die andere. Obwohl die Atome hinsichtlich der elektrischen Kräfte, die uns experimentell in
der Regel zur Verfügung stehen, sehr steif sind, findet eine kleine Gesamtverschiebung der Ladungsschwerpunkte statt. Diese kleine Verschiebung wollen
wir jetzt abschätzen. Dafür brauchen wir eine konkrete Beschreibung eines
gebundenen Elektrons. Wir wissen, dass die korrekte Beschreibung nur durch
die Quantenmechanik möglich ist. In einfachen Fälle lässt sich aber ein gebundenes Elektron durch ein Modell beschreiben, das wir kennen. Wir verteilen
das Elektron als ’Wolke’ um das Proton. Der Schwerpunkt dieser Wolke liegt
am Ort des Protons, um die Ladungsneutralität des Atoms zu ermöglichen.
Da es sich um ein gebundenes Elektron handelt, wird jede Verschiebung der
Elektronenwolke von einer rücktreibenden Kraft erschwert. Wir setzen diese Kraft proportional zur Verschiebung x. Dann können wir ein gebundenes
Elektron mit der uns wohl bekannten Gleichung mẍ + mω 2 x = 0 beschreiben. Durch Gleichsetzung von h̄ · ω mit der Bindungsenergie des Elektrons
erhält die Proportionalitätskonstante ω eine genaue physikalische Bedeutung.
Der genaue Wert der Bindungsenergie lässt sich allerdings nur anhand der
Quantenmechanik berechnen: deshalb ist das, was wir hier brauchen, um ein
Atom zu beschreiben, ein Modell mit einem zu bestimmenden Parameter
ω. Wir tauchen jetzt unser Atom in ein konstantes elektrisches Feld E und
berechnen, wie sich der Elektronenschwerpunkt verschiebt: genau für eine
solche Rechnung ist dieses Modell brauchbar (das lässt sich zeigen, wenn
man unser Resultat mit der quantenmechanischen Berechnung vergleicht!!).
Wir müssen die Gleichung mẍ + mω 2 x = q · E lösen. Die einfachste Lösung
ist selbstverständlich die Konstante δ = qE/mω 2 , welche die Verschiebung
82
KAPITEL 5. ELEKTROSTATIK
des Schwerpunktes unter der Wirkung eines konstanten Feldes angibt (man
denke an eine Masse, die an einer Feder hängt und unter der Wirkung der
Gravitation steht). Die Verschiebung ist proportional zu E und zu q. Als
Resultat dieser Verschiebung bildet sich eine räumliche Ladungsinhomogenität entlang der von E vorgegebenen Richtung im Inneren des Isolators, der
selbst ein elektrisches Feld erzeugt. Diese Ladungsinhomogenität nennt man
elektrischen Dipolmoment
.
2 .
~
~
p~ = q · ~δ = q 2 E/mω
= α · ε0 E
wobei die Materialkonstante α die Polarisierbarkeit des Atoms darstellt. Die
Anwesenheit atomarer Dipolmomente p~i am Ort i wird, in einem KontinuumLimes, durch die Einführung eines Polarisationsdichtevektors P~ (~r) berücksichtigt, mit ~pi = P~ (~r) · dV . Somit schreibt sich das gesamte Potential einer
Ladungsverteilung, welche auch Dipole enthält, als
Φ(~r) =
1
4πǫ0
Z
dV ′
h
P~ (~r′ ) · (~r − ~r′ ) i
ρ(~r′ )
+
| ~r − ~r′ |
| ~r − ~r′ |3
Den zweiten Term können wir durch eine Identität der Vektoranalysis umformen:
~ ′ P~ (~r′ )
∇
1
1
1
~ ′ P~ (~r′ ) + P~ (~r′ ) · ∇
~′
=
∇
| ~r − ~r′ |
| ~r − ~r′ |
| ~r − ~r′ |
Nehmen wir an, dass P~ in einem endlichen Raum lokalisiert ist. Dann können
wir den Gaussschen Satz benutzen, um das Integral über die Divergenz auszuwerten. Sein Beitrag verschwindet. Somit ist das Potential einer Ladunsgverteilung mit P~ (~r) 6= 0
Φ(~r) =
1
4πǫ0
Z
dV ′
h ρ(~
~′
r′) − ∇
· P~ (~r′ ) i
| ~r − ~r′ |
Das ist der Ausdruck für das Potential einer effektiven Ladungsverteilung
~ · P~ ): das 1. Gesetz der Elektrostatik erhält einen zusätzlichen Term
(ρ(~r) − ∇
. ~ ~
ρpol = −∇ · P .
~ ·E
~ = 1 [ρ − ∇
~ · P~ ]
∇
ǫ0
Diese extra effektiven Polarisationsladungen müssen bei der Lösung elektrostatischer Probleme zur Ermittlung elektrischer Felder berücksichtigt werden: u.a. sind sie selbstverstndlich an der Aufstellung der Randbedingungen
beteiligt.
83
KAPITEL 5. ELEKTROSTATIK
Der Plattenkondensator mit Dielektrikum
Wir führen die Suche nach Polarisationsladungen in der einfachen Geometrie eines Plattenkondensators, welcher mit einem homogenen Dielektrikum
P~ (~r) = P~0 = ρ0 ~p gefüllt wird (ρ0 : Dichte des Isolators). Für p~ kann man das
~ einsetzen (E
~ ist dann das elektrische Feld am
induzierte Dipolmoment ǫ0 ·α· E
Ort des Dipols). Später werden wir permanente Dipolmomente untersuchen:
die Resultate dieses Abschnittes sind aber von der Art von p~ unabhängig.
~ · P~ = ∂Pz . Für Pz (z) setzen wir Pz = P0 im InneIn dieser Geometrie ist ∇
∂z
ren der Platte und Pz = 0 ausserhalb, siehe Figur. Somit ist die Divergenz
P
d
P0
z
d
Abbildung 5.11: Pz fällt innerhalb der Dicke δ von P0 auf 0.
von P~ an den Rändern des Dielektrikums konzentriert, und zwar beträgt sie
P0
bei −d/2 und − Pδ0 bei d/2. Die dazugehörige effektive Polarisationslaδ
dung ist demnach in dünnen Schichten am Rand des Isolators konzentriert,
und zwar besteht eine effektive positive Ladungdichte Pδ0 bei d/2 und eine
negative bei −d/2. Wir sind jetzt bereit, durch die Einführung einer geeigneten Gaussschen Schachtel, die elektrischen Felder zu berechnen. Die Sym~ entlang z ist. Wir haben auch eine
metrie des Problems suggeriert, dass E
vollständige Idee, wo und wie viele Ladungen sich befinden. Auf den Kondensatorplatten haben wir die Ladungsdichte ±σf rei , unmittelbar daneben
die Polarisiationsdichten ρpol = ∓ Pδ0 . Anwendung des Gaussschen Gesetzes
auf die Fläche S1 liefert eine Gleichung für E0 : E0 = σf rei /ε0 . Anwendung
auf die Fläche S2 liefert eine Bestimmungsgleichung für E:
E · A = (σ · A − ρpol · A · δ)/ε0
Für den Fall P0 = ρ0 ǫ0 · α · E erhalten wir
E=
E0
1 + ρ0 · α
84
KAPITEL 5. ELEKTROSTATIK
S2
S1
Metall
+++++++++++++++++++++++++
E0
-----------------------------E
Isolator
+++++++++++++++++++++++++
-----------------------------Metall
Abbildung 5.12: Konstruktion der Gausschen Flächen
Die Materialkonstante ρ0 · α heisst elektrische Suszeptibilität χ. Die Konstante κ = 1 + χ heisst Dielektrizitätskonstante. Die Spannung zwischen den Kondensatorplatten ist U = Uf rei /κ. Somit ist die Kapazität
C = Cf rei · κ. Wird ein Plattenkondensator von einem Dielektrikum bei
konstanter Plattenladung ausgefüllt, sinkt die Spannung.
Die Gleichung κ = 1 + ρ0 α setzt eine makroskopische Grösse (die Dielekq2
trizitätskonstante) mit atomaren Eigenschaften (α = ε0 ·m·ω
2 ) in Verbindung.
Damit können wir Messungen der Dielektrizitätskonstante benutzen, um etwas über atomare Eigenschaften der Materie zu erfahren. Unsere Formel ist
natürlich nur eine sehr grobe Näherung, weil wir ein Modell gewählt haben,
das quantenmechanische Komplikationen unberücksichtigt lässt. Beispielsweise haben wir angenommen, dass ein Atom nur eine Resonanzfrequenz
hat, während es in Wirklichkeit viele hat. Um die Polarisierbarkeit der Atome
ordentlich zu berechnen, müssen wir die vollständige Quantentheorie anwenden. Die oben angeführten klassischen Ideen liefern uns aber eine vernünftige
Abschätzung. Sehen wir, ob wir die Grössenordnung der Dielektrizitätskonstanten von einigen Substanzen bestimmen können. Versuchen wir es mit
Wasserstoff. Die Bindungsenergie - d.h. die Energie, die notwendig ist, um
das Wasserstoffatom zu ionisieren - beträgt bekanntlich 13.6 eV. Daher folgt:
ω = 2·1016 Hz. Wenn wir nun diesen Wert für die Berechnung von κ benutzen,
erhalten wir κ = 1.00022 (in einem Gas bei Normaldruck und -Temperatur
(1 Atm, 0 C) befinden sich 2, 69 · 1019 Atome/cm3 ). Der Messwert der Dielektrizitätskonstanten für Wasserstoffgas beträgt 1.00026. Eine weniger allgemeine Version der Maxwell Gleichungen für die Elektrostatik lässt sich aus
der Beobachtung herleiten, dass der Effekt der Polarisationsladungen durch
Division der freien Ladungsdichte durch κ · ε0 statt durch ε0 simuliert werden
85
KAPITEL 5. ELEKTROSTATIK
~ ·E
~ = ρf rei /(κ · ε0 ).
kann (in einigen einfachen Fällen): ∇
Moleküle mit einem permanenten Dipolmoment.
Als Nächstes betrachten wir ein Molekül, das ein permanentes Dipolmoment
aufweist - so wie das Wassermolekül. Die Ladungstrennung ist eine Folge der
- O
H
+
H
H2O
+
Abbildung 5.13: Ladungsverteilung in einem H2 O Molekül
chemischen Bindung und nicht eines angelegten elektrischen Feldes. In einem
Wassermolekül finden wir beispielsweise eine negative Nettoladung auf dem
Sauerstoffatom und eine positive Nettoladung auf jedem der beiden Wasserstoffatome, die nicht symmetrisch, sondern wie in der Figur angeordnet sind.
Obwohl die gesamte Ladung des ganzen Moleküls Null ist, hat diese eine Ladungsverteilung mit einem kleinen Überschuss an negativer Ladung auf der
einen Seite und einem kleinen Überschuss an positiver Ladung auf der anderen. Diese Anordnung bildet einen Dipol: die Ladungstrennung findet statt,
obwohl kein E Feld vorhanden ist. In Abwesenheit eines elektrischen Feldes
zeigen die einzelnen Dipole statistisch in alle Richtungen, so dass das Gesamtmoment pro Einheitsvolumen Null ist. Wird aber ein elektrisches Feld
angelegt, so geschieht zweierlei: Erstens wird aufgrund der Kräfte, die auf
die Elektronen wirken, ein zusätzliches Dipolmoment induziert. Dabei erhalten wir genau dieselbe Art von Elektronenpolarisation, wie wir sie bei einem
nicht-polaren Molekül festgestellt haben. In einer sehr genauen Untersuchung
müsste dieser Effekt natürlich berücksichtigt werden; wir werden ihn aber im
Augenblick vernachlässigen. Zweitens hat das elektrische Feld die Tendenz,
die einzelnen Dipole auszurichten und erzeugt so ein Gesamtmoment pro
Einheitsvolumen. Wären alle Dipole eines Gases ausgerichtet, so gäbe es eine
sehr starke Polarisation, aber das kommt in Gasen nicht vor. Bei gewöhnlichen Temperaturen und elektrischen Feldern verhindern die Zusammenstösse
der Moleküle, verursacht durch ihre Wärmebewegung, dass sie sich stark ausrichten. Es gibt aber eine gewisse Gesamtausrichtung und daher auch eine
gewisse Polarisation. Die auftretende Polarisation kann mit den Methoden
86
KAPITEL 5. ELEKTROSTATIK
der statistischen Mechanik berechnet werden. Um diese Methoden zu verwenden, müssen wir die Energie eines Dipols in einem elektrischen Feld kennen.
Betrachten wir einen Dipol mit dem Moment p~ in einem elektrischen Feld,
siehe Figur. Die Energie der positiven Ladung ist q · Φ(1) und die Energie
E
+q (1)
d
-q (2)
Abbildung 5.14: Energie eines Dipols im elektrischen Feld
der negativen Ladung −q · Φ(2). Die Energie des Dipols ist daher
Epot = q · Φ(1) − q · Φ(2)
~
= q · d~ · ∇Φ
~
= −~p · E
Wir bezeichnen den thermischen Mittelwert von p~ bei einer bestimmten Tem~ Feld entlang z angelegt ist, erwarten wir
peratur mit < p~ >. Da das E< p~ >= (0, 0, p0· < cos ϑ >). Für Wasser ist p0 = 6 · 10−30 C · m. ϑ ist
~ einen
der Winkel zwischen p~ und der z-Richtung. Die W-keit, dass ~p mit E
Winkel ϑ aufspannt, hängt von der Temperatur ab: nach W.Gibbs ist diese
W-keit (kB Boltzmannschekonstante, kB = 1.38 · 10−23 Joule/K)
∝e
−Epot (ϑ)
kB ·T
Somit ist
< pz > = p 0 ·
R
sin ϑdϑdϕ cos ϑep·E·cosϑ/kB T
R
sin ϑdϑdϕep·E·cosϑ/kB T
Für normale Temperaturen und Felder ist der Exponent klein: durch die
Taylor-Entwicklung der Exponentialfunktion erhalten wir schlussendlich
< Pz >=
ρ0 · p20 · E
3 · kB · T
KAPITEL 5. ELEKTROSTATIK
Somit ist die Polarisationsdichte proportional der Feldstärke E: χ =
ρ ·p2
87
ρ0 ·p20
3·ǫ0 ·kB ·T
und κ = 1 + 3·ǫ00·kB0·T . Auch hängt die Polarisation erwartungsgemäss von
der reziproken Temperatur ab, weil bei höheren Temperaturen wegen der
Zusammenstösse weniger Ausrichtung möglich ist. Diese T −1 Abhängigkeit
nennt man das Curie Gesetz.
Eine interessante Anwendung von festen Dielektrika mit einem permanenten Dipolmoment ist die Piezoelektrizität. Dieser Effekt benutzt die Tatsache, dass in gewissen
Materialien (sog. Ferroelektrika) die permanente Dipole vollständig ausgerichtet sind. Eine
mechanische Spannung, der ein Kristall unterworfen ist, ändert dessen elektrischen Polarisation. Umgekehrt verursacht auch ein an den Kristall angelegtes elektrisches Feld in ihm
eine mechanische Verzerrung. Ein schematisches Beispiel eines piezoelektrischen Kristalls
ist in der Figur gegeben. Der nicht beanspruchte Kristall hat eine dreizählige Symme-
Abbildung 5.15: Piezoelektrizität
trieachse. Die Pfeile bedeuten Dipolmomente. Die Summe der drei Dipolmomente eines
jeden Schnittpunktes ist Null. Wird der Kristall einem elektrischen Feld ausgesetzt, so
entsteht in der angegebenen Richtung eine Polarisation. Die Polarisation verursacht eine
mechanische Dehnung: Es gilt typischerweise △l/l = E · η (△l/l = prozentuelle elastische
Dehnung; η ≈ 10−7 − 10−9 cm/V = piezoelektrische Koeffizient). Piezokristalle sind in
der modernen Forschung und Technologie sehr nützlich: sie werden zum Beispiel in Rastertunnelmikroskopen benutzt, um kleine und kontrollierte Bewegungen durchzuführen.