2. Klausur Physik Leistungskurs Klasse 11 14.1.2014

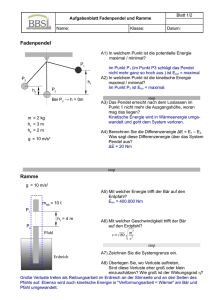
2. Klausur Physik Leistungskurs Klasse 11
14.1.2014
Dauer. 90 min
Teil 1
Hilfsmittel: alles verboten
1.
a) Schreiben Sie den Energieerhaltungssatz für ein abgeschlossenes System auf. (2)
b) Ein Auto wird ohne angezogene Handbremse und ohne eingelegten Gang auf einer leicht
abschüssigen Straße abgestellt. Das Auto fängt von alleine an zu Rollen und kommt auf dem
waagerechten Teil der Straße wieder zum Stehen.
Schreiben Sie für die Zahlen 1 bis 15 die richtigen Begriffe auf. (5)
Vor dem Losrollen hat das Auto nur __1__ Energie. Während es den Berg hinunter fährt,
wandelt es die __2__ Energie in __3__ Energie und in ___4___ um. Die __5__ Energie
entsteht durch __6__ und die __7__ durch Reibungsarbeit.
Am Ende des Hügels ist die ___8__ Energie bezüglich dem geraden Straßenabschnitt gleich
__9__. Das Auto hat auf Grund seiner __10__ nur noch __11___ Energie.
Auf dem waagerechten Straßenteil wandelt das Auto seine __12__ Energie vollständig in
__13__ durch __14__ um. Wenn das Auto wieder steht, ist die komplette potentielle Energie
vor dem Losrollen in Wärmeenergie umgewandelt worden. Diese Energie ist nicht mehr
nutzbar und wird als ___15___ Energie bezeichnet.
2. Gleich schwere Pakete werden vom
Fußboden in ein Regal gehoben, dessen Fächer
untereinander den gleichen Abstand haben.
Welche der Arbeiten sind gleich groß? (siehe
Abbildung) (3)
Hinweis: Es werden Lösungen in der Form
1=2=5
erwartet.
3. Begründen Sie, warum der Quotient aus F und s als Maß für die mechanische Arbeit nicht sinnvoll
wäre. (2)
F: Kraft, um einen Körper zu bewegen
s: Strecke, um den der Körper bewegt wird.
4. Ein Pendel wird um die Höhe h gehoben
und losgelassen. Beim Durchlaufen der
Nulllage stößt der Faden an ein Hindernis,
dass das Pendel verkürzt.
Wie hoch schwingt der Pendelkörper auf
der anderen Seite? (1)
a) höher als h
b) wieder bis h
c) niedriger als h.
Teil 2
Hilfsmittel: Tafelwerk, Taschenrechner
5. Zeigen Sie ausführlich, welcher Wasserstrom in l/min erforderlich ist, wenn bei einem
Gefälle von 4,5 m bei einer Wasserturbine eine Leistung von 70 kW abgenommen werden
soll?
Der Turbinenwirkungsgrad beträgt 80 %. (6)
6. Ein PKW kommt mit 72 km/h durch eine Waldkurve gefahren. Der Fahrer sieht in 30 m
Entfernung einen umgestürzten Baum quer auf der Straße liegen. Er benötigt 0,3s
Reaktionszeit und bremst dann.
a) Welchen Weg legt der Fahrer während der Reaktionszeit zurück? (2)
b) Zeigen Sie ausführlich, wie groß die Bremsbeschleunigung sein muss, um genau am
Baum zum Stehen zu kommen? (4)
c) Zeigen Sie ausführlich, wie groß dafür die notwendige Haftreibungszahl sein muss. (4)
d) Zu allem Übel hat es geregnet, so dass die Reibungszahl auf 0,3 sinkt.
Wie groß ist die Bremsbeschleunigung jetzt?
Geben Sie die Geschwindigkeit an, mit der das Auto auf den Baum prallt. (4)
e)Wie viel Prozent seiner ursprünglichen Bewegungsenergie hat das Auto beim Aufprall? (1)
Lösungen
1. a) In einem abgeschlossenen System ist die Summe aller Energien immer konstant.
Abgeschlossenes System: Über die Systemgrenzen werden weder Stoffe noch Energie
transportiert.
Das ist praktisch nicht möglich, die Thermoskanne (Dewargefäß) realisiert diese Bedingung
für einen kurzen Zeitraum.
b) Vor dem Losrollen hat das Auto nur 1:potenzielle Energie. Während es den Berg hinunter
fährt, wandelt es die 2:potenzielle Energie in 3:kinetische Energie und in 4:Wärmeenergie
um. Die 5:kinetische Energie entsteht durch 6:Beschleunigungsarbeit und die
7:Wärmeenergie durch Reibungsarbeit.
Am Ende des Hügels ist die 8:potenzielle Energie bezüglich dem geraden Straßenabschnitt
gleich 9:Null. Das Auto hat auf Grund seiner 10:Geschwindigkeit nur noch 11:kinetische
Energie.
Auf dem waagerechten Straßenteil wandelt das Auto seine 12:kinetische Energie vollständig
in 13:Wärmeenergie durch 14:Reibungsarbeit um. Wenn das Auto wieder steht, ist die
komplette potentielle Energie vor dem Losrollen in Wärmeenergie umgewandelt worden.
Diese Energie ist nicht mehr nutzbar und wird als 15:entwertete Energie bezeichnet.
Epot -> Ewärme+Ekin->Ewärme
1
potenzielle Energie
2
potenzielle Energie
3
kinetische Energie
4
Wärmeenergie
5
kinetische Energie
6
Beschleunigungsarbeit
7
Wärmeenergie
8
potenzielle Energie
9
Null
10
Geschwindigkeit
11
kinetische Energie
12
kinetische Energie
13
Wärmeenergie
14
Reibungsarbeit
15
entwertete Energie
2.
2-3
4-8
5-6
3. Die Arbeit ist umso größer, je mehr Kraft man aufbringen muss und je größer der Weg ist,
um den man etwas bewegt.
Nimmt man den Quotienten aus Kraft und Weg, würde bei einem kleiner werdenden Weg
das Ergebnis der Berechnung, also die Arbeit immer größer.
Wenn man das Produkt aus beiden Größen nimmt, steigt das Ergebnis der Berechnung im
gleichen Maße, wie die Arbeit größer wird. Doppelter Weg bringt also auch doppelte Arbeit.
4. b) wieder bis h
In der Höhe h hat das Pendel potenzielle Energie. Schwingt es nach unten, wandelt es diese
in kinetische Energie um. Am tiefsten Punkt ist die gesamte potenzielle Energie in kinetische
umgewandelt worden.
Nach diesem Punkt läuft der Vorgang umgekehrt ab, kinetische Energie wird in potenzielle
umgewandelt. Dabei kann die potenzielle Energie des Schwingungskörpers nur den Wert
erreichen, der am Anfang vorhanden war.
Die potenzielle Energie in beiden Umkehrpunkten ist also gleich groß, egal, ob das Pendel
unterwegs am Hindernis verkürzt wird oder nicht.
Die potenzielle Energie ist aber nur von der Masse des Körpers und der Höhe h abhängig.
Da sich die Masse bei diesem Versuch nicht geändert hat, bleibt auch die Höhe gleich.
5.
geg.:
h = 4,5 m
ges.:
m
P = 70 kW
η = 0,8
t = 60 s
Lösung: Das Wasser besitzt in 4,5 m Höhe eine bestimmte potentielle Energie,
die beim Herabstürzen in kinetische Energie umgewandelt wird. Diese
Energie wird in der Wasserturbine in elektrische Energie umgewandelt.
Die Leistung des herabstürzenden Wassers muss also so groß sein wie
die elektrische Leistung der Turbine (unter Berücksichtigung des
Wirkungsgrades!)
Pel = Pmech ⋅ η
Pel =
E pot ⋅ η
t
m ⋅ g ⋅h ⋅ η
Pel =
t
P ⋅t
m = el
g⋅h ⋅ η
m=
70 ⋅10 3 W ⋅ 60 s
9,81 sm2 ⋅ 4,5 m ⋅ 0,8
m = 119 ⋅10 3 kg
Antwort: Da ein Kilogramm Wasser einem Volumen von einem Liter entspricht,
müssen pro Minute 119 000 Liter herabstürzen.
6.
geg.:
Lösung:
ges.:
µ
km
m
= 20
h
s
s = 30m
tR = 0,3 s
a) Durch die Reaktionszeit von 0,3 s verkürzt sich der eigentliche Bremsweg.
s
v=
t
s = v ⋅t
v = 72
s = 20 ms ⋅ 0,3 s
s = 6m
Damit verkürzt sich der eigentliche Bremsweg auf 24 m.
Um das Auto nun auf dieser Strecke zum Halten zu bringen, muss eine bestimmte
negative Beschleunigung (Bremsbeschleunigung) erreicht werden. Diese
Beschleunigung wird nach dem Grundgesetz der Mechanik durch eine Kraft, der
Bremskraft, aufgebracht. Die Bremskraft wirkt vom Auto über Reibung auf die
Straße, die nach dem Wechselwirkungsgesetz die gleich große Gegenkraft
aufbringen muss. Ist die Reibungszahl zu klein, kann sie das nicht und das Auto
rutscht. Dadurch wird aber die geforderte Beschleunigung nicht erreicht und das
Auto kommt nicht zum Stillstand. Aber so weit sind wir noch nicht.
Zuerst die Beschleunigung. Es gilt:
v = a ⋅ t und
a
s = ⋅ t2
2
Durch Umstellen und Einsetzen erhält man
v2
a=
2⋅s
( 20 ms )
a=
2
2 ⋅ 24m
m
a = 8,3 2
s
Diese Beschleunigung wird durch die Bremskraft erreicht. Es gilt:
F =m⋅a
Die Bremskraft wiederum wird durch die Reibungskraft zwischen Reifen und Straße
aufgebracht. Für die Reibungskraft gilt:
F = µ ⋅ FN
FN ist die Normalkraft, also die Kraft, mit der ein Körper auf seine Unterlage
(Straße) drückt. Da die Straße keine Steigung hat, ist sie gleich der Gewichtskraft:
F = µ ⋅m⋅ g
Beide Kräfte sind nach dem Wechselwirkungsgesetz gleich groß und können
deshalb gleichgesetzt werden:
m ⋅a = µ ⋅m⋅ g
a = µ⋅g
µ=
µ=
a
g
8,3 sm2
9,81 sm2
µ = 0,85
b) Ist die Reibungszahl vorgegeben, kann man die mögliche Beschleunigung
bestimmen. Daraus lässt sich über den zur Verfügung stehenden Bremsweg die
Aufprallgeschwindigkeit berechnen.
Beschleunigung:
m ⋅ a = µ ⋅m ⋅ g
a = µ⋅g
a = 0,3 ⋅ 9,81
m
s2
m
s2
Da dieses eine Bremsbeschleunigung ist, schreibt man
m
a = − 2,94 2
s
Die negative Beschleunigung reduziert die Geschwindigkeit. Es gilt allgemein:
∆v
a=
∆t
v −v
a= 2 1
t 2 − t1
v2 ist die Endgeschwindigkeit, also die, mit der das Auto auf den Baum fährt. v1 ist
die Anfangsgeschwindigkeit, also die 20 m/s. Die Zeitspanne t2-t1 ist die Zeit vom
Beginn der Bremsung bis zum Auffahren und wird einfach als t geschrieben.
Die Geschwindigkeit v 2 ist die gesuchte Größe, also wir die Gleichung danach
umgestellt.
v −v
a= 2 1
t
a ⋅ t = v 2 − v1
a = 2,94
v 2 = v1 + a ⋅ t
Das heißt, die Aufprallgeschwindigkeit ist die ursprüngliche Geschwindigkeit plus
eines Werts a ⋅ t . Da a aber negativ ist (negative Beschleunigung), wird von der
ursprünglichen Geschwindigkeit etwas abgezogen.
In der Gleichung für die gesuchte Geschwindigkeit v 2 fehlt noch die Zeit für den
Bremsvorgang. Es gilt die Gleichung
a
s = ⋅ t 2 + v1 ⋅ t
2
Der hintere Ausdruck wäre der Weg ohne Bremsen, der vordere Teil bewirkt durch
die negative Beschleunigung eine Verringerung dieses Weges.
Die Gleichung muss nach der Zeit umgestellt werden. Das geübte Auge sieht eine
quadratische Gleichung:
Mit dieser Geschwindigkeit kracht das Auto auf den Baum.
Die kinetische Energie des Autos berechnet sich mit
m
Ekin = ⋅ v 2
2
Da die Masse unverändert bleibt, gilt:
a
s = ⋅ t 2 + v1 ⋅ t
2
a
0 = ⋅ t 2 + v1 ⋅ t − s
2
2 ⋅ v1
2⋅s
0 = t2 +
⋅t −
a
a
2
v
 v  2⋅s
t1 =− 1 ±  1  +
2
a
a
a
2
m
m 

 20 s 
2 ⋅ 24m
s
t1 =−
± 
 +
m
m
2
 − 2,94  − 2,94 m
− 2,94 2
s
s2 
s2

Das sieht schlimmer aus als es ist. Wichtig beim Rechnen ist die konsequente
Berücksichtigung der Vorzeichen.
20
t 1 = 6,81s ± 46,28 s2 − 16,33 s2
2
t 1 = 6,81s ± 5, 47 s
2
t1 = 1,34 s
t 2 = 12,28 s
Die erste Zeit ist die Zeit für den Zusammenstoß. Damit kann nun die
Geschwindigkeit berechnet werden:
v 2 = v1 + a ⋅ t
m
m
+ ( −2,94 2 ⋅1,34 s)
s
s
m
v 2 = 16,1
s
km
v 2 = 57,8
h
Mit dieser Geschwindigkeit kracht das Auto auf den Baum.
Die kinetische Energie des Autos berechnet sich mit
m
Ekin = ⋅ v 2
2
Da die Masse unverändert bleibt, gilt:
Ekin ~ v 2
Das Verhältnis von zwei Energien ist deshalb gleich dem Verhältnis der Quadrate
der Geschwindigkeiten.
v 2 = 20
2
(16,1 ms )
2
( 20 ms )
= 0,66
Das sind noch 66% der ursprünglichen Energie.
Antwort:
Die Reibungszahl zwischen Reifen und Straße muss mindestens 0,85 betragen.
Das entspricht den üblichen Werten bei trockener Straße.
Auf nasser Straße prallt das Auto mit etwa 57,8 km/h auf den Baum und besitzt
noch 66% seiner ursprünglichen Energie.