1. Kontrolle Physik Grundkurs Klasse 11 Arbeit und

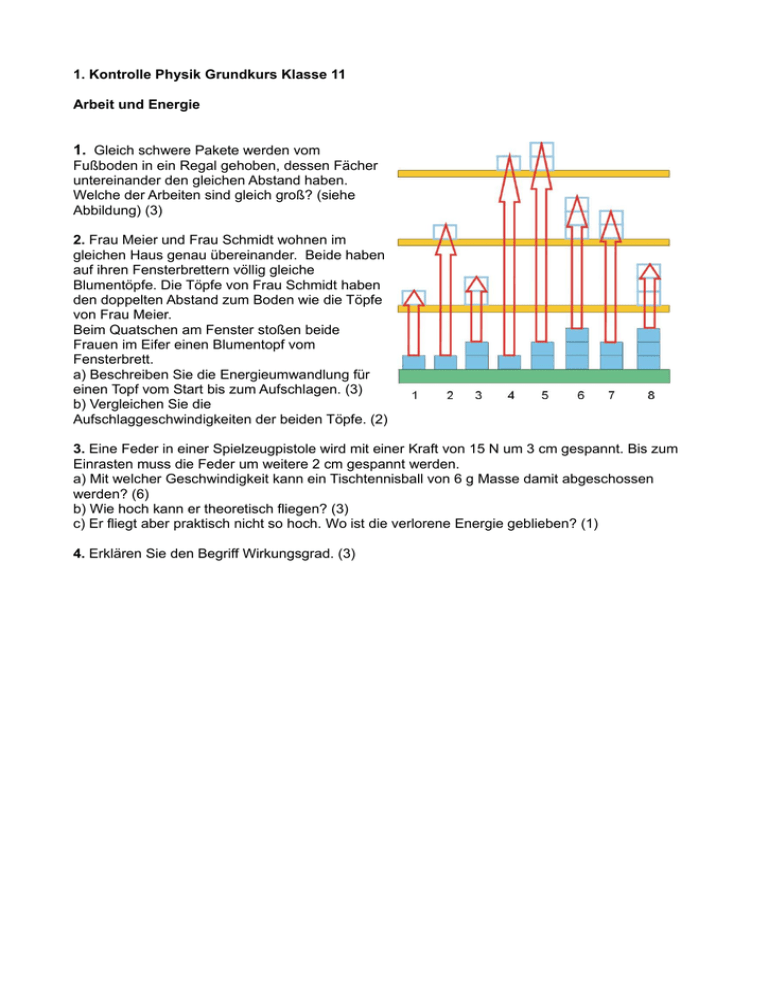
1. Kontrolle Physik Grundkurs Klasse 11
Arbeit und Energie
1. Gleich schwere Pakete werden vom
Fußboden in ein Regal gehoben, dessen Fächer
untereinander den gleichen Abstand haben.
Welche der Arbeiten sind gleich groß? (siehe
Abbildung) (3)
2. Frau Meier und Frau Schmidt wohnen im
gleichen Haus genau übereinander. Beide haben
auf ihren Fensterbrettern völlig gleiche
Blumentöpfe. Die Töpfe von Frau Schmidt haben
den doppelten Abstand zum Boden wie die Töpfe
von Frau Meier.
Beim Quatschen am Fenster stoßen beide
Frauen im Eifer einen Blumentopf vom
Fensterbrett.
a) Beschreiben Sie die Energieumwandlung für
einen Topf vom Start bis zum Aufschlagen. (3)
b) Vergleichen Sie die
Aufschlaggeschwindigkeiten der beiden Töpfe. (2)
3. Eine Feder in einer Spielzeugpistole wird mit einer Kraft von 15 N um 3 cm gespannt. Bis zum
Einrasten muss die Feder um weitere 2 cm gespannt werden.
a) Mit welcher Geschwindigkeit kann ein Tischtennisball von 6 g Masse damit abgeschossen
werden? (6)
b) Wie hoch kann er theoretisch fliegen? (3)
c) Er fliegt aber praktisch nicht so hoch. Wo ist die verlorene Energie geblieben? (1)
4. Erklären Sie den Begriff Wirkungsgrad. (3)
Lösungen
1.
2-3
4-8
5-6
2. a) steht der Topf auf dem Fensterbrett, hat er potenzielle Energie. Beim Fallen wird diese immer
kleiner, da der Abstand zum Boden kleiner wird. Gleichzeitig wird der Topf immer schneller, am ihm
wird also Beschleunigungsarbeit geleistet. Dadurch gewinnt er an kinetischer Energie. Beim
Aufschlagen ist die gesamte potenzielle Energie in kinetische Energie umgewandelt worden.
b) Wenn die Blumentöpfe noch friedlich auf den Fensterbänken stehen, haben beide im Vergleich
zum Boden potenzielle Energie. Da die potenzielle Energie direkt proportional zur Höhe ist, besitzt
der obere Topf die doppelte Menge an Energie.
Beim Fallen wandelt jeder Topf diese Energie vollständig in Bewegungsenergie um. Es gilt also:
E kin = E pot
Die Gleichungen für diese beiden Energie kann man einsetzten und nach der gesuchten
Geschwindigkeit umstellen:
m 2
⋅ v = m ⋅ g⋅ h
2
v = 2 ⋅ g⋅ h
Die Masse kürzt sich raus, da bei Vernachlässigung der Luftreibung die Masse des fallenden
Körpers keine Rolle spielt.
Mit der Gleichung erkennt man den Zusammenhang zwischen Geschwindigkeit und Höhe:
v~ h
Der eine Topf hat die doppelte Höhe des anderen, also z.B. 1 und 2. Damit ist die
Auftreffgeschwindigkeit des oberen Topfe nur
2 = 1,4
mal so groß wie die Geschwindigkeit des unteren Topfes und nicht etwa doppelt so groß.
Über die Überlebenschancen der Töpfe sagt das natürlich gar nichts.
3.
geg.:
F = 15N
ges.:
s1 = 3 ⋅ 10− 2 m
a) v
b) h
s2 = 5 ⋅ 10 − 2 m
m = 6 ⋅ 10− 3 kg
Lösung:
a) Beim Abschießen der Pistole wird die Federspannenergie in Beschleunigungsarbeit
umgewandelt. Wenn der Ball die Mündung verlässt, hat er kinetische Energie.
Es gilt also:
Esp = Ekin
1
1
D ⋅ s22 = m ⋅ v 2
2
2
Die Federkonstante D kann aus den gegebenen Größen bestimmt werden:
D=
F
s1
eingesetzt und umgestellt:
1F 2 1
⋅ s2 = m ⋅ v 2
2 s1
2
F 2
⋅ s2 = m ⋅ v 2
s1
v2 =
F ⋅ s22
s1 ⋅ m
v=
F ⋅ s22
s1 ⋅ m
Damit kann die gesuchte Geschwindigkeit berechnet werden:
v=
(
15N ⋅ 5 ⋅ 10− 2 m
)
2
3 ⋅ 10 − 2 m ⋅ 6 ⋅ 10 − 3 kg
v = 14,4
m
s
b) Diese kinetische Energie wird über Hubarbeit in potenzielle Energie umgewandelt:
Ekin = Epot
1
m⋅ v2 = m⋅ g⋅ h
2
1 2
v = g⋅ h
2
v2
h=
2⋅ g
2
m

 14,4 s 

h= 
m
2 ⋅ 9,81 2
s
h = 10,6m
Antwort:
Der Tischtennisball verlässt die Pistole mit 14,4 m/s und fliegt theoretisch 10,6 m hoch.
Praktisch kommt er nicht in diese Höhe, da durch die Luftreibung kinetische Energie
über Reibungsarbeit in Wärmeenergie umgewandelt wird.
4. Bei jedem Arbeitsprozess wird eine Energieform in eine andere umgewandelt. Es ligt also immer
eine Ausgangsenergie und eine Nutzenergie vor. Bei jeder dieser Energieumwandlungen wird
gleichzeitig noch ein Teil der Ausgangsenergie in Wärmeenergie umgewandelt. Das erfolgt
meistens durch Reibung.
Diese Wärmeenergie ist nicht oder nur schwer nutzbar, also für den eigentlichen Vorgang verloren.
Der Wirkungsgrad gibt das Verhältnis von Nutzenergie und Ausgangsenergie an. er kann nie
größer oder gleich 1 sein.