Mechanik II Herbst 2010

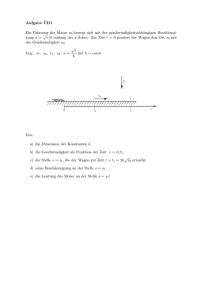
Aufgabe D1
v
Ein Fahrzeug verzögert seine Geschwindigkeit
mit einer geschwindigkeitsabhängigen Beschleunigung, die durch die im nebenstehenden
Diagramm gegebene Parabel beschrieben werden kann.
.
v0
Geg.: v0 , a1 mit a1 < 0 , v2 mit 0 < v2 < v0
0
a1
0
a
Ges.:
Bestimmen Sie
a) die Zeit τ , nach der sich die Geschwindigkeit auf die Hälfte des Anfangswertes v0
reduziert hat,
b) das Weg-Zeit-Gesetz s(t) und die Strecke sτ = s(τ ), die das Fahrzeug in der Zeit τ
zurückgelegt hat,
c) den Sicherheitsabstand, der beim Beginn des Bremsen nötig ist, um durch den
Bremsvorgang gerade nicht auf ein mit konstanter Geschwindigkeit v2 vorausfahrendes Fahrzeug aufzufahren!
∫
Hinweis:
√
2 √
1
dx = −
1 − c1 x + const
c1
1 − c1 x
Aufgabe D2
Eine homogene Scheibe 1 mit Masse m1 und Trägheitsmoment JS1 ist in ihrem Schwerpunkt im Gelenk A drehbar gelagert und bei B mit einem Balken der Masse m2 und dem
Trägheitsmoment JS2 gelenkig verbunden. Zum Zeitpunkt t = 0 wird das System aus der
skizzierten Ruhelage im Schwerefeld der Erde losgelassen.
Annahmen: Alle Gelenke seien reibungsfrei, die Massenverteilung in den Bauteilen
homogen.
Geg.: b , m1 , JS1 , r , m2 , JS2 , ⃗g
m1, JS1
r
A
g
S1
s
B
x
s
m2, JS2
S2
b
Ges.:
Bestimmen Sie für den Zeitpunkt unmittelbar nach dem Loslassen (Zeitpunkt t = 0+ )
a) die Winkelbeschleunigung der Scheibe 1
b) die Winkelbeschleunigung der Scheibe 2
c) die Auflagerkraft bei A,
d) die Schnittreaktionen im Balken 2 im Schnitt S: S als Funktion der Koordinate x !
Aufgabe D3
Eine homogene Scheibe mit Masse m und Trägheitsmoment JS ist über eine Feder
mit der Federsteifigkeit c und ungespannter Länge x0 einem Dämpfer mit der
Dämpfungskonstanten β zwischen zwei feststehenden Wänden W1 und W2 eingebaut. Die Scheibe hat bei B Kontakt mit einer Unterlage, die mit s(t) relativ zu den
Wänden oszilliert.
Annahmen: Alle Gelenke seien reibungsfrei. Federkraft und Dämpferkraft seien ideal,
also der Auslenkung x − x0 bzw. der Geschwindigkeit ẋ proportional. Die Scheibe bewege
sich, ohne auf der Unterlage zu rutschen.
Geg.: r , m, JS , c, x0 , β , ⃗g , s(t) = s0 sin(Ωt) mit s0 , Ω
g
m, JS
r
c
β
W1
W2
S
x
s(t)
B
Ges.:
Bestimmen Sie
a) die Winkelgbeschleunigung der Scheibe als Funktion von ẍ, s̈ und r (Abrollbedingung),
b) die Differentialgleichung der erzwungenen Bewegung der Scheibe,
c) die Kreisfrequenz des freien Scheibe-Feder-Dämpfer-Systems !
Musterlösung Mechanik II SS10
Aufgabe D1
11 Punkte
a) Mit der Definitionsgleichung a =
dt =
dv
folgt nach Trennung der Variablen:
dt
√
dv
a(v)
mit
a(v) = a1
1−
v
v0
(a1 < 0)
Integration liefert:
∫τ
′
v∫0 /2
dt = τ =
v0
t=0
dv
2v0
√
=−
v
a1
a1 1 −
v0
√
v
1−
v0
v0 /2
v0 √
=
2
− a1
v0
b) Das Weg-Zeit-Gesetz erhält man
√ zum Beispiel durch Integration der Defintionsgleichung
2v0
v(t)
ds = v(t) dt. Laut a) gilt t =
. Dies nach v(t) umgestellt und integriert liefert
1−
− a1
v0
(
s(t) − s0 = v0 t 1 −
Damit wird s(τ ) =
1 ( a1 )2 2 )
t
3 2v0
1 v02 √
2.
3 − a1
Alternativ leifert ein Ansatz mit der Beziehung ds =
!
mit s(t0 ) = s0 = 0.
v dv
dieselbe Lösung.
a(v)
c) Minimaler Sicherheitsabstand
(
1 ( a 1 )2 2 )
ts zurück,
3 2v0
in der das vorausfahrende Fahrzeug die Strecke s2 = v2 ts zurücklegt. Sollen sie sich nicht
berühren, unterscheidet sich die Strecken um den Sicherheitsabstand ss und die Fahrzeuge
haben die gleiche Geschwindigkleit v2 . Dies sind zwei Gleichungen für die beiden unbekannten
ts und ss .
Das gebremste Auto legt in der Zeit ts die Strecke s1 (ts ) = v0 ts 1 −
(
s1 (ts ) = s2 (ts ) + ss
→
v 0 ts 1 −
v1 (ts ) = v2
→
v0 −
1 ( a 1 )2 2 )
ts − v2 ts = ss
3 2v0
a21 2
t = v2
4v0 s
(1)
(2)
Aufgabe D2
25 Punkte
a)
Drallsatz für Scheibe 1:
JS1 φ̈1 = −Bx r
m2 a2x = −Bx
Schwerpunktsatz Balken 2:
Freischnitt Scheibe 1
(1)
(2)
Euler: ⃗a2 = ⃗aB + ⃗aS2 ,B
G1 Ax
in x-Richtung: a2x = aBx − aS2 ,Bx
b 2
φ̇7
= 0 folgt:
= 2 2
a2x = −rφ̈1
1
ϕ1, ϕ1
0
mit aBx = −rφ̈1 und aS2 ,Bx
1
Ay
By
Bx
(3)
Freischnitt Balken 2
Aus (1), (2) und (3) folgt: φ̈1 = 0
a2y
By ϕ2, ϕ2
Bx
G2
1
b)
Drallsatz für Balken 2:
JS2 φ̈2 = −By
Schwerpunktsatz Balken 2:
b
2
Kinematik Balken 2
1
aBy
Euler: ⃗a2 = ⃗aB + ⃗aS2 ,B
in y-Richtung: a2y = aBy − aS2 ,By
a2y
aBx
aS2,Bx
0
b
2
7
mit aBy = r φ̇
φ̈2 = 0 folgt:
1 = 0 und aS2 ,By =
2
Aus (4), (5) und (6) folgt:
(6)
aBy
B =0
m2 g b/2
φ̈2 =
JS2 + m2 b2 /4
1
Mb
aBx=0
L
x
JS2
JS2 + m2 b2 /4
Ax = −Bx = 0
= 0 = Ay − G1 + By , By = m2 g
m1 aS1 x = 0 = Ax + Bx ,
a2x
aS2,By
Freischnitt B.-Teilstück
c) Schwerpunktsatz in x- und y-Richtung:
m1 aS1 y
a2x
(4)
m2 a2y = −By − G2 (5)
b
a2y = − φ̈2
2
1
d) Schnittreaktionen:
m2 (b − x)
b−x 2
ã2x =
−L ,
ã2x = (x +
) φ̇2 = 0
b
2
m2 (b − x)
m2 (b − x)
b−x
ã2y = −Q −
g , ã2y = (x +
) φ̈2
b
b
2
b−x
(b − x)3
J2 φ̈2
=
+Mb − Q
,
J2 = JS2
2
b3
ϕ 2 , ϕ2
Q
~
a2y
1
a~2x
G2(b-x)/b
Kontrolle bei x = 0:
√
b
ã2x = ( ) φ̇22 = 0
2
√
b
= −Q − m2 g = −By − m2 g , ã2y = ( ) φ̈2
2
√
b
=
+Mb − Q ,
J2 = JS2
2
m2 ã2x =
m2 ã2y
J2 φ̈2
−L = Bx ,
Kontrolle bei x = b:
0 =
−L
0 =
−Q
0 = +Mb
√
√
√
Aufgabe D3
13 Punkte
a)
Euler: ⃗aS = ⃗aB + ⃗aS,B
ϕ, ϕ
G
in x-Richtung: aSx = ẍ , aBx = s̈ , aS,Bx = rφ̈
⇒
φ̈ =
S
FF
ẍ − s̈
r
x, x
FR
1
1
1
aB,Sx
s
R
N
b)
Drallsatz für Scheibe um den Schwerpunkt: JS φ̈ = +R r
Schwerpunktsatz für Scheibe in x-Richtung: m ẍ = −FF − FR − R
Federkraft: FF = c(x − x0 )
Dämpferkraft: FR = β ẋ
Mit der neuen Koordinate ξ = x − x0 von der statischen Ruhelage aus gemessen folgt
wegen ξ˙ = ẋ , ξ¨ = ẍ:
(m + JS /r2 ) ξ¨ + β ξ˙ + c ξ = JS /r2 s0 Ω2 sin(Ωt)
c) Kreisfrequenz des freien Scheibe-Feder-Dämpfer-Systems:
Homogene D’gl: (m + JS /r2 ) ξ¨ + β ξ˙ + c ξ = 0
Der Lösungsansatz x = C exp(λt) liefert die Charakteristische Gleichung:
λ2 +
β
c
λ+
=0
2
m + JS /r
m + JS /r2
β
Die Eigenwerte lauten λ1,2 = −
±
2(m + JS /r2 )
sich eine Schwingung einstellt, falls
√
√
β2
c
−
, so dass
4(m + JS /r2 )2 m + JS /r2
√
β2
c
−
= iω 2 mit i = −1
2
2
2
4(m + JS /r )
m + JS /r
√
Die Eigenkreisfrequenz des gedämpften Schwingers ist daher: ω =
β2
c
−
m + JS /r2 4(m + JS /r2 )2
1