Energie- und Wärmetechnik Inhaltsverzeichnis 1

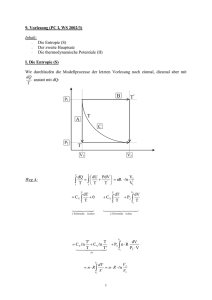
Energie- und Wärmetechnik
Inhaltsverzeichnis
1. Thermodynamische Grundlagen
1.1. Abgeschlossene, geschlossene und offene Systeme
1.2. Volumenänderungsarbeit, Verschiebearbeit, Technische Arbeit
Anwendung: Umkehrosmose
1.3. Zustandsgrößen, Erster und Zweiter Hauptsatz
Anwendung: Solaranlage
1.4. Thermodynamische Grundprozesse, Arbeits- und Wärmediagramm
2. Kraft- und Arbeitsmaschinen mit idealen Gasen
2.1. Eigenschaften idealer Gase
2.2. Bewertung von Kraftmaschinenprozessen
2.3. Technisch wichtige Kraftmaschinenprozesse mit idealen Gasen
2.3.1. Gasturbinenprozesse
2.3.2. Stirling-Prozeß
2.3.3. Otto- und Dieselprozeß
2.4. Bewertung von Arbeitsmaschinenprozessen
2.5. Technisch wichtige Arbeitsmaschinenprozesse mit idealen Gasen
3. Kraft- und Arbeitsmaschinen mit Dämpfen
3.1. Eigenschaften von Dämpfen
3.2. Dampftafeln und Diagramme
3.3. Technisch wichtige Kraftmaschinenprozesse mit Dämpfen
3.3.1. Dampfturbinenprozeß
3.3.2. GUD-Prozeß
3.4. Technisch wichtige Arbeitsmaschinenprozesse mit Dämpfen
3.4.1. Kältemittel
3.4.2. Kältemaschinen und Wärmepumpen
3.4.3. Absorptionskältemaschinen (Beispiel: Zeolith-Systeme)
4. Aktuelle Entwicklungen in der Energiebereitstellung und –umwandlung
4.1. Kraft-Wärme-Kopplung und Blockheizkraftwerke
4.2. MHD-Generator
4.3. Brennstoffzellen
5. Grundlagen der Wärmeübertragung
Literatur zum Thema „Energie- und Wärmetechnik”
1.
Cerbe/Hofmann, Einführung in die Wärmelehre
Hanser-Verlag, München
2.
Stephan/Mayinger, Thermodynamik
Band 1: Einstoffsysteme
Band 2: Mehrstoffsysteme und chemische Reaktionen
Springer-Verlag, Berlin
3.
Bejan, Advanced Engineering Thermodynamics
John Wiley, New York
4.
Herbrik, Energie- und Wärmetechnik
Teubner-Verlag, Stuttgart
5.
Thomas, Thermische Kraftanlagen
Springer-Verlag, Berlin
6.
Kalide, Kraft- und Arbeitsmaschinen
Hanser-Verlag, München
Prozesse der Energieumwandlung
Potentielle Energie
(Lageenergie,
chemische Energie,
Kernenergie)
Wasser-, Wind- und
Gezeitenkraftanlagen
Pumpen
Umkehrosmose
Mechanische
Energie
Verbrennung
Kernreaktionen
Therm. Solaranlagen
Kraftmaschinen
(Motoren und
Turbinen)
Wärme
Arbeitsmaschinen
(Kälteanlagen und
Wärmepumpen)
Generatoren
Absorptionskälteanlagen und
-wärmepumpen
Brennstoffzellen
Photovoltaik
Eektrolyse
Tauchsieder
MHDGenerator
Elektromotoren
Elektrische
Energie
Technische Arbeit am Beispiel eines Kompressors:
Eintrittsstelle 1:
Druck p1 → Druckkraft F1 = p1A1 →
Verschiebearbeit W1 = F1s1 = p 1 A 1
V1
= p 1 V1 > 0
A1
(zugeführt)
Austrittsstelle 2:
Druck p2 → Druckkraft F2 = p2A2 →
Verschiebearbeit W2 = −F2s2 = − p 2 A 2
V2
= − p 2 V2 < 0
A2
(abgeführt)
Flächenaddition:
p 2 V2 +
V1
∫
pdV = p 1 V1 +
V2
p2
∫ Vdp
p1
Technische Arbeit:
p2
Wt,12 = + ∫ Vdp > 0
p1
Volumenänderungsarbeit:
V2
Wv,12 = − ∫ pdV > 0
V1
Es ergibt sich:
Wt,12 = WV,12 + p2 V2 − p1 V1
Bei Kompression ist also Wt,12 die über die Antriebswelle
zuzuführende Arbeit. Sie beinhaltet die Verschiebearbeiten.
Bei Flüssigkeiten ist bei Kompression ∆V ≈ 0, also Wv,12 ≈ 0.
Dann gilt:
Wt,12 ≈ (p 2 − p 1 )V
Osmose und Umkehrosmose
Osmose
gebremste Osmose
ρg∆h = π
ρg∆h' = π - ∆p
Umkehrosmose
ρg∆h" = ∆p - π
* : Semipermeable Membran aus Celluloseacetat oder Polyamid
Die Porengrößen der
Membranen betragen etwa
1 nm.
Sie werden mit Drücken
bis zu 50 bar
beaufschlagt.
Osmotische Drücke verschiedener Meerwässer:
Mittelmeer:
π ≈
Totes Meer:
π ≈ 500 bar
Totes Meer (1:1 verdünnt):
π ≈ 130 bar
50 bar
Grundbegriffe der Thermodynamik
Thermische Zustandsgrößen: Druck p, Volumen V, Temperatur T
Kalorische Zustandsgrößen: Innere Energie U
Enthalpie H:
H = U + pV
2
∫
Entropie S:
S 2 − S1 =
Freie Energie F:
F = U – TS
1
dQ rev
T
Freie Enthalpie G: G = H - TS
Prozeßgrößen:
Wärme Q, Arbeit W
Druck und Temperatur sind „intensive” Größen. Für die „extensiven”
(masseproportionalen) Größen Volumen, Energie, Wärme, Arbeit und
Entropie werden Spezifische Größen definiert:
ν =
V
1
U
H
S
F
G
Q
W
=
; u =
; h =
; s =
; f =
; g =
; q =
; w =
m
ρ
m
m
m
m
m
m
m
Arbeit und Wärme: positiv, wenn dem System zugeführt
negativ, wenn vom System abgeführt
1. Hauptsatz:
für geschlossene Systeme: dQ + dWv = dU oder Q12 + Wv,12 = U2 – U1
für offene Systeme:
2. Hauptsatz:
dQ + dWt = dH oder Q12 + Wt,12 = H2 – H1
dQ rev
dQ irr
>
oder TdS > dQirr
T
T
2
2
dQ rev
dQ irr
oder S 2 − S1 = ∫
> ∫
T
T
1
1
dS =
2. Hauptsatz in 1. Hauptsatz eingesetzt:
TdS + dWv ≥ dU → dWv ≥ dU – TdS
TdS + dWt ≥ dH → dWt ≥ dH – TdS
Das Gleichheitszeichen gilt
bei reversibler Prozeßführung
dU – TdS bzw. dH - TdS ist also
- entweder die kleinste für einen gewünschten Prozeß zu
investierende Volumenänderungsarbeit bzw. Technische Arbeit
- oder sein Betrag ist die größte bei einem Prozeß zu
gewinnende Volumenänderungsarbeit bzw. Technische Arbeit.
Bei isothermen Prozessen wird:
dWv ≥ dF und dWt ≥ dG
Thermodynamische Gleichgewichtsbedingungen:
Wird einem System keine Volumenänderungsarbeit bzw. Technische
Arbeit zugeführt oder entnommen, so ist dF = 0 bzw. dG = 0.
Definition der mittleren spezifischen Wärmekapazität
ϑ2
ϑ2
∫
ϑ
c m ϑ2
1
c dϑ =
ϑ1
ϑ
c m ϑ2
1
→
⋅ (ϑ 2 − ϑ 1)
∫
=
c dϑ
ϑ1
ϑ2 − ϑ1
In den Tabellenwerken sind in der Regel Mittelwerte der spezifischen Wärmekapazitäten zwischen einer festen unteren Temperaturgrenze und einer variablen oberen Temperaturgrenze tabelliert. Die Mittelwerte zwischen beliebigen Temperaturgrenzen
können daraus exakt berechnet werden.
Beispiel für die feste Untergrenze 0°C:
Intergralzerlegung liefert:
ϑ2
∫
c dϑ =
ϑ1
0° C
∫
c dϑ +
ϑ2
∫
c dϑ =
0° C
ϑ1
ϑ2
∫
c dϑ −
0° C
ϑ1
∫
c dϑ
0° C
Daraus folgt:
ϑ2
ϑ
c m ϑ2
1
=
∫
0° C
c dϑ −
ϑ1
∫
c dϑ
0° C
=
ϑ2 − ϑ1
cm
ϑ2
0° C
⋅ ϑ2 − cm
ϑ2 − ϑ1
ϑ1
0° C
⋅ ϑ1
Mit dem Mittelwert kann dann wie mit einer Konstanten gerechnet
werden:
ϑ2
ϑ2
ϑ1
ϑ1
Q12 = m ∫ c dϑ = m c m
(ϑ 2 − ϑ 1)
Strahlungsbilanz der Erde (Niehaus 1975; Kleemann/Meliß 1988).
Im Mittel durchdringen nur 47 % der Sonnenstrahlung als direkte oder
diffuse Strahlung die Erdatmosphäre.
Die Summe beider Anteile heißt Globalstrahlung G G .
kW
Die Solarkonstante G 0 = 1,35 2
ist die Strahlungsleistung pro
m
Flächeneinheit über den gesamten Wellenlängenbereich auf eine Fläche
außerhalb der Atmosphäre bei senkrechtem Einfall.
Für eine unter dem Winkel ϕ geneigte Fläche gilt: G 0,g = G 0 ⋅ cos ϕ
Unter Berücksichtigung der geographischen Breite und bei Mittelung
über
Tag
und
Nacht
ergibt
sich
für
Süddeutschland
als
kWh
kWh
Jahresmittelwert der Globalstrahlung: G G Jahr ≈ 1050 2
≈ 2,9 2
m ⋅ a
m ⋅ d
Jahresgang der
Globalstrahlung
und ihrer Komponenten: Die
diffuse Strahlung
überwiegt in
unseren Breiten
deutlich.
Schema eines
Flachkollektors
G G,g ist die Globalstrahlungsintensität auf die geneigte Fläche
(üblich in W/m2), Q N die Nutzwärmeleistung, τ der Transmis-
sionskoeffizient der Deckscheibe, α der Absorptionskoeffizient
der Absorberwand, ϑU die Umgebungstemperatur und AK ist die
Kollektorfläche.
Es wird in der Regel mit einem "isothermen" Kollektormodell
gerechnet, d.h. die Temperaturdifferenz ∆ϑK zwischen Kollektoreintritt und -austritt liegt zwischen 2 und 4°C.
Die Nutzwärmeleistung, die an einem Solarkollektor abgegriffen
werden kann, beträgt:
Q N = ατG G,g A K − Q V = ατG G,g A K − ξ m A K(ϑ A − ϑ U )
Dabei ist Q V die Verlustwärmeleistung, ξm der mittlere Wärmeübergangskoeffizient, ϑA die Temperatur der Absorberwand, die
geringfügig höher als die Austrittstemperatur des Kollektorfluids ist. η0 = ατ heißt Konversionsfaktor.
Der Kollektorwirkungsgrad ist definiert als:
η =
Q N
ξ (ϑ − ϑ U )
ξ (ϑ − ϑ U )
= ατ − m A
= η0 − m A
G G,g A K
G G,g
G G,g
Meßergebnisse des
Wirkungsgrades an
realen Kollektoren
µ: Schwarznickel
∇: Schwarzlack
Schema einer solaren Warmwasserbereitungsanlage
Der Regler stellt den Massenstrom durch den Kollektor nach der
Temperaturdifferenz zwischen Kollektorausgang und Speicherausgang ein. Zwischen Speicher und Warmwasserwärmetauscher ist
ein Zwischenkreis geschaltet, damit die Zusatzheizung nur ein
kleines Volumen aufzuheizen hat.
Schema einer Thermosiphonanlage.
Durch den Dichteunterschied zwischen Kollektoreingang und Kollektorausgang wird ein konvektiver Massenstrom des Arbeitsfluids
erzeugt.
Solche
Anlagen
sind
bis
zu
einer
Kollektorfläche von 10 m2 geeignet. Sie reagieren allerdings
etwas träge auf Änderungen der solaren Einstrahlung.
Zur Funktion einer Thermosiphonanlage:
Der Volumenstrom durch ein Rohrleitungssystem der Gesamtlänge
L ist nach dem Hagen-Poiseuilleschen Gesetz:
πR 4
V =
∆p
8ηd L
∆p = Hg(ρ0 − ρ1)
mit
R ist dabei der Rohrradius, ηd die dynamische Zähigkeit.
Im typischen Temperaturbereich von 15 bis 60°C ist die
Dichteänderung proportional zu ∆Tk = T1 - T0:
ρ0 − ρ1 = βρ0 ∆TK ;
Also wird
πR 4Hg
V =
βρ0 ∆TK
8ηd L
β ist der Volumenausdehnungskoeffizient des Arbeitsfluids.
Unter Annahme einer nur sehr geringen Dichteänderung ergibt
sich der Massenstrom als:
π R 4Hg
βρ 20 ∆ TK
m ≈ V ρ 0 =
8η d L
(Thermosiphoneffekt)
Andererseits gilt für die Nutzwärmeleistung:
ηG G,g A K
K ∆ TK ;
Q N = ηG G,g A K = mc
Also ist:
m =
c K ∆ TK
(Gl.1)
(Gl.2)
Darin ist η der Kollektorwirkungsgrad und ck die spezifische
Wärmekapazität des Kollektorfluids.
Wegen
des
Thermosiphon-Effekts steigt der Massenstrom
mit zunehmender Temperaturdifferenz. Steigender Massenstrom bewirkt aber im Kollektor
ein
Absinken
der
Temperaturdifferenz. Der Arbeitspunkt ist der Schnittpunkt beider Linien.
Elimination von ∆Tk aus den Gleichungen (1) und (2) ergibt:
m =
R 2ρ 0
2
π HgβηG G,g A K
2η d Lc K
;
Also gilt:
m ∝
G G,g
Der Massenstrom paßt sich also der Globalstrahlung an.
Gesamtbewertung von solaren Warmwasserbereitern:
Die Kostenanalyse eines Systems zur solaren
Warmwasserbereitungmuß folgende Kostenelemente
berücksichtigen:
Einmalig:
• Kollektorkosten
• Wärmespeicherkosten
• Kosten für Armaturen und Rohrleitungen
• Kosten für Struktur und Dichtung
• Reglerkosten
• Installationskosten
Laufend:
• Betriebskosten
• Kosten der Zusatzheizung
• Abschreibung
Die Gesamtkosten steigen stärker als proportional zur
Kollektorfläche vor allem wegen der Wärmespeicherkosten und
der Kosten für Struktur und Dichtung.
Deshalb ergibt eine Gesamtkostenbilanz ein Minimum bei relativ
kleinen
Kollektorflächen.
In
der
Abbildung
werden
Thermosiphonund
Pumpenanlagen
mit
einem
elektrischen
Durchlauferhitzer verglichen. Es ist dabei sowohl für die
Zusatzheizung
als
auch
für
den
Durchlauferhitzer
ein
Strompreis von 0,15 €/kWh zugrunde gelegt.
Typische Anlagendaten:
• Warmwasserbedarf pro Tag 200 l
• erforderliche Leistung 1,2 kW
• Kollektorfläche 5 m2
• Speichervolumen 250 l
• Zapftemperatur 45°C
• Zulauftemperatur 12°C
• Über das Jahr gemittelte solare Deckungsrate ca. 60 %