I.1 Elektromagnetische Strahlung - lehrer.uni

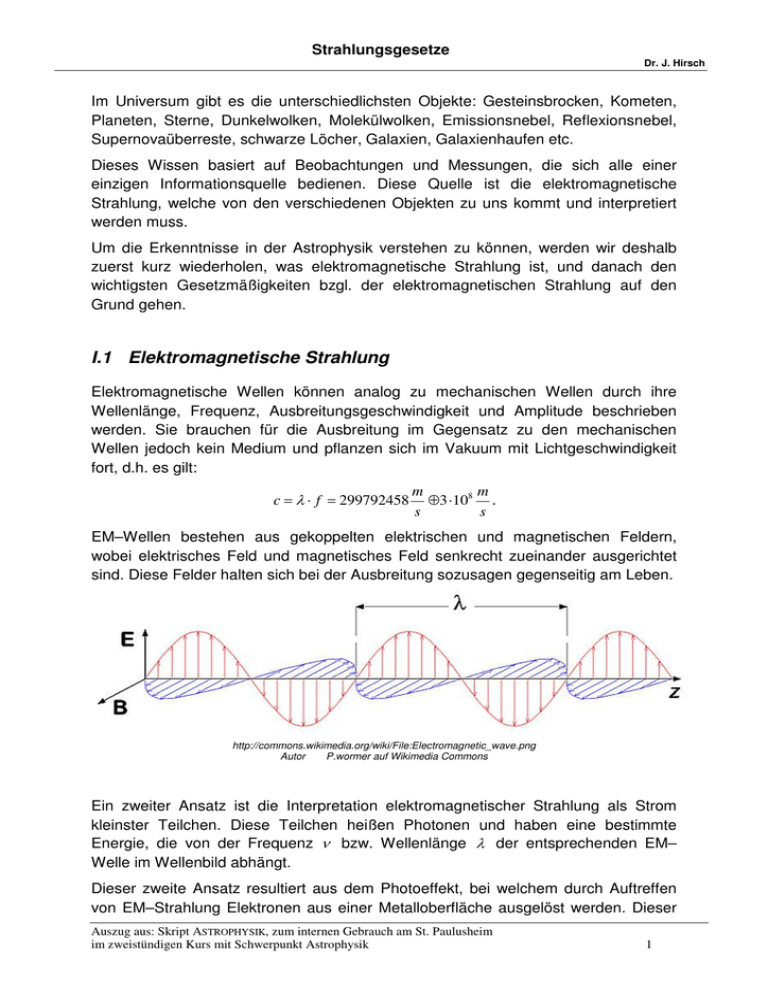
Strahlungsgesetze
Dr. J. Hirsch
Im Universum gibt es die unterschiedlichsten Objekte: Gesteinsbrocken, Kometen,
Planeten, Sterne, Dunkelwolken, Molekülwolken, Emissionsnebel, Reflexionsnebel,
Supernovaüberreste, schwarze Löcher, Galaxien, Galaxienhaufen etc.
Dieses Wissen basiert auf Beobachtungen und Messungen, die sich alle einer
einzigen Informationsquelle bedienen. Diese Quelle ist die elektromagnetische
Strahlung, welche von den verschiedenen Objekten zu uns kommt und interpretiert
werden muss.
Um die Erkenntnisse in der Astrophysik verstehen zu können, werden wir deshalb
zuerst kurz wiederholen, was elektromagnetische Strahlung ist, und danach den
wichtigsten Gesetzmäßigkeiten bzgl. der elektromagnetischen Strahlung auf den
Grund gehen.
I.1 Elektromagnetische Strahlung
Elektromagnetische Wellen können analog zu mechanischen Wellen durch ihre
Wellenlänge, Frequenz, Ausbreitungsgeschwindigkeit und Amplitude beschrieben
werden. Sie brauchen für die Ausbreitung im Gegensatz zu den mechanischen
Wellen jedoch kein Medium und pflanzen sich im Vakuum mit Lichtgeschwindigkeit
fort, d.h. es gilt:
c = λ ⋅ f = 299792458
m
m
≈ 3 ⋅108 .
s
s
EM–Wellen bestehen aus gekoppelten elektrischen und magnetischen Feldern,
wobei elektrisches Feld und magnetisches Feld senkrecht zueinander ausgerichtet
sind. Diese Felder halten sich bei der Ausbreitung sozusagen gegenseitig am Leben.
http://commons.wikimedia.org/wiki/File:Electromagnetic_wave.png
Autor
P.wormer auf Wikimedia Commons
Ein zweiter Ansatz ist die Interpretation elektromagnetischer Strahlung als Strom
kleinster Teilchen. Diese Teilchen heißen Photonen und haben eine bestimmte
Energie, die von der Frequenz ν bzw. Wellenlänge λ der entsprechenden EM–
Welle im Wellenbild abhängt.
Dieser zweite Ansatz resultiert aus dem Photoeffekt, bei welchem durch Auftreffen
von EM–Strahlung Elektronen aus einer Metalloberfläche ausgelöst werden. Dieser
Auszug aus: Skript ASTROPHYSIK, zum internen Gebrauch am St. Paulusheim
im zweistündigen Kurs mit Schwerpunkt Astrophysik
1
Strahlungsgesetze
Dr. J. Hirsch
Effekt kann nicht mit dem Wellenbild erklärt werden, da nicht die Intensität des Lichts
(Amplitude gibt im Prinzip die Energie an) die Energie der ausgelösten Elektronen
bestimmt, sondern einzig die Frequenz des Lichts dafür verantwortlich ist. Für die
Erklärung des Photoeffekts mithilfe des Teilchenmodells (1905) erhielt Albert Einstein
1921 den Nobelpreis für Physik.
Bis heute hat übrigens jedes Instrument, dessen Genauigkeit es zulässt, gezeigt,
dass Licht bzw. EM–Strahlung definitiv aus Photonen besteht. Da sich bestimmte
Phänomene wie die Interferenz oder Beugung allerdings nicht im Teilchenmodell
erfassen lassen, versucht man in der Quantenmechanik oder in der Quantenelektrodynamik (QED), diese beiden Eigenschaften zu vereinen. Dabei wird der
Begriff der Flugbahn eines Photons durch eine Welle (genauer Wellenfunktion)
ersetzt, welche die Ausbreitung der Teilchen im Raum beschreibt. Genauere
Ausführungen würden an dieser Stelle jedoch zu weit gehen.
Zusammenfassend halten wir fest, dass sich bestimmte Phänomene für uns nur in
einem der beiden Bilder der EM–Strahlung erklären lassen (Welle–Teilchen–
Dualismus):
Strahlung als Welle
Strahlung als Teilchen
Die Wellenlänge λ und die Frequenz f
hängen über die Beziehung c = λ ⋅ f
zusammen.
Die Strahlung besteht aus Photonen der
c
Energie E = h ⋅ f = h ⋅ , wobei λ und f
λ
aus dem Wellenbild stammen. Dabei ist
h das Plancksche Wirkungsquantum (
h = 6, 626069 ⋅10−34 Js ).
I.2 Stefan-Boltzmann-Gesetz
Trifft Strahlung auf einen Körper, so wird ein Teil der Strahlung reflektiert oder
gestreut, ein bestimmter Anteil dieser Strahlung jedoch vom Körper absorbiert.
Dadurch erhöhen sich seine innere Energie und damit auch seine Temperatur.
Jeder Körper mit einer Temperatur über den absoluten Nullpunkt ( 0 K = −273,15°C )
strahlt aber auch eine gewisse Energiemenge in Form von Strahlung ab, meist
Wärmestrahlung im Infrarotbereich.
Der Quotient aus absorbierter Strahlungsleistung und emittierter Strahlungsleistung
heißt Absorptionsgrad α und entspricht dem Emissionsgrad ε des Körpers:
α=
absorbierteStrahlungsleistung
=ε
emittierteStrahlungsleistung
Der Absorptionsgrad eines Körpers hängt vom Material des Körpers, der Größe und
Beschaffenheit seiner Oberfläche, ihrer Temperatur und von der Wellenlänge der
Strahlung ab.
Auszug aus: Skript ASTROPHYSIK, zum internen Gebrauch am St. Paulusheim
im zweistündigen Kurs mit Schwerpunkt Astrophysik
2
Strahlungsgesetze
Dr. J. Hirsch
Ein Körper, der über alle Wellenlängen jegliche Strahlung absorbiert, hat den
Absorptionsgrad α = 1 und heißt Schwarzer Körper bzw. Schwarzer Strahler. Ein
solcher Körper existiert in der Natur nicht, sondern ist eine Idealisierung. Dennoch
werden Sterne als Schwarzer Körper simuliert und lassen sich mit den Gesetzen für
Schwarzkörperstrahlung relativ gut beschreiben.
Das Stefan-Boltzmann-Gesetz (benannt nach Josef Stefan und Ludwig Boltzmann)
stellt
für einen Schwarzen
Körper eine
Beziehung zwischen
der
Gesamtstrahlungsleistung P, der Oberfläche A und der Temperatur T her:
P = σ ⋅ A ⋅T 4 .
Man erkennt, dass die Strahlungsleistung eines Schwarzen Körpers proportional zur
vierten Potenz seiner Temperatur ist. Dies bedeutet zum Beispiel, dass bei einer
zehnfach höheren Temperatur die 104 = 10000 –fache Leistung abgestrahlt wird.
Die Proportionalitätskonstante heißt Stefan-Boltzmann-Konstante und ist eine
Naturkonstante:
σ = 5, 670 4·10−8
W
.
m2K 4
I.3 Plancksches Strahlungsgesetz
Hat ein Schwarzer Körper eine
Temperatur T > 0 K , so gibt er Energie
in Form von Strahlung ab. Es ist jedoch
nicht so, dass ein Schwarzer Körper mit
einer bestimmten Temperatur Strahlung
mit einer ganz bestimmten Wellenlänge
emittiert, sondern immer über das
gesamte
Frequenz–
bzw.
Wellenlängenspektrum. Betrachtet man
die Intensität bzw. Strahlungsleistung
gegenüber
der
Wellenlänge
aufgetragen, fällt auf, dass die
Plancksche Funktion bei einer ganz
bestimmten Wellenlänge ein Maximum
hat (s. Abbildung unten). Ein schwarzer
Körper strahlt also bei einer ganz
bestimmten Wellenlänge am stärksten.
http://commons.wikimedia.org/wiki/File:BlackbodySpectrum_lin_150dpi_de.png
Autor
Sch auf Wikimedia Commons
Auszug aus: Skript ASTROPHYSIK, zum internen Gebrauch am St. Paulusheim
im zweistündigen Kurs mit Schwerpunkt Astrophysik
3
Strahlungsgesetze
Dr. J. Hirsch
I.4 Wiensches Verschiebungsgesetz
Die Planck–Funktion lässt sich mathematisch beschreiben durch
PT ( f ) =
2⋅h⋅ f 3
⋅
c2
1
e
h⋅ f
k ⋅T
bzw.
−1
PT ( λ ) =
2⋅h⋅c
λ
3
1
⋅
e
h ⋅c
k ⋅T ⋅λ
.
−1
Berechnet man mit Hilfe der Differentialrechnung die Wellenlänge λmax , bei welcher
der Hochpunkt der Planck–Funktion liegt, so erhält man die Abhängigkeit
λmax ⋅ T = 2,898 ⋅10−3 m ⋅ K .
Die Lage des Strahlungsmaximums wird also ausschließlich von der Temperatur
bestimmt, wobei sich das Maximum zu kleineren Wellenlängen verschiebt, wenn die
Temperatur des Schwarzen Körpers steigt. Dieses Gesetz heißt Wiensches
Verschiebungsgesetz.
Dieses Gesetz ist zur Bestimmung der Oberflächentemperatur von Sternen
ungemein nützlich. Misst man über ein breites Frequenzintervall die Intensität, so
lässt sich die für diesen Stern charakteristische Planck–Funktion zeichnen und
anhand der Lage des Maximums die Temperatur des Sterns berechnen. (Eigentlich
genügen dafür sogar zwei Intensitätsmessungen bei unterschiedlichen Frequenzen.)
Übrigens:
Berechnet man die Fläche unter der Planck–Funktion im Frequenzintervall [0; ∞] , so
erhält man die pro Einheitsfläche abgegebene Strahlung, d.h. das Stefan–
Boltzmann–Gesetz:
∞
∫ P ( f ) df
T
= σ ⋅T 4 .
0
Auszug aus: Skript ASTROPHYSIK, zum internen Gebrauch am St. Paulusheim
im zweistündigen Kurs mit Schwerpunkt Astrophysik
4