Lorentzkraft
Werbung

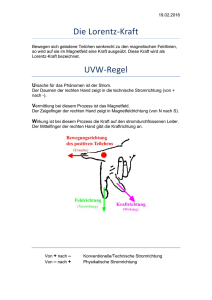
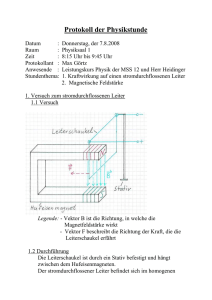
Lorentzkraft 1. Die Doppelleiterschaukel 1 Das nebenstehende Bild zeigt eine doppelte Leiterschaukel. Das sind zwei Leiterschaukeln, die leitend durch zwei Kupferstangen miteinander verbunden sind. Das horizontale Stück jeder der beiden Leiterschaukeln befindet sich jeweils im Feld eines sehr starken Permanentmagneten. Wir betrachten nun die rechte Leiterschaukel. Der Hufeisenmagnet hat unten einen Süd– und oben einen Nordpol. Nun wird die Leiterschaukel nach links bewegt. Daraufhin bewegt sich die linke Leiterschaukel nach rechts. Wie muss demzufolge das Magnetfeld des linken Hufeisenmagneten orientiert sein? Doppelleiterschaukel 2. Die Doppelleiterschaukel 2 Das nebenstehende Bild zeigt eine doppelte Leiterschaukel. Das sind zwei Leiterschaukeln, die leitend durch zwei Kupferstangen miteinander verbunden sind. Das horizontale Stück jeder der beiden Leiterschaukeln befindet sich jeweils im Feld eines Permanentmagneten. Nun wird die rechte Leiterschaukel nach links bewegt. Wieso und wohin bewegt sich der linke Teil der Doppelleiterschaukel, der sich im Magnetfeld befindet? ~l F F~r Magnetfeld b Magnetfeld Am Ort der rechten Leiterschaukel weist das Magnetfeld nach unten. Die Elektronen im Leiter erfahren eine Kraft nach links. Dadurch entsteht ein Strom. Dabei weist die technische Stromrichtung in die Zeichenebene. Am Ort des linken Lösung: Leiters weist dann die technische Stromrichtung aus der Zeichenebene. Die Kraft ist nach Vorraussetzung nach rechts gerichtet. Mit der ,,rechten Hand–Regel” findet man dann, dass das Magnetfeld nach unten gerichtet ist. Doppelleiterschaukel 1 Lösung: Durch die Bewegung der rechten Leiterschaukel nach links wird in dieser ein Strom induziert, wobei die technische Stromrichtung aus der Zeichenebene weist. Weil beide Leiterschaukeln leitend miteinander verbunden sind, fließt auch in der linken Leiterschaukel ein Strom. Dieser ist in der linken Leiterschaukel in die Zeichenebene gerichtet. Ein stromdurchflossener Leiter in einem Magnetfeld erfährt eine Kraft. Mit der ,,rechten–Hand– Regel” findet man, dass die Kraft auf die linke Leiterschaukel nach rechts weist. 3. Ein kugelförmiges Staubkorn mit dem Radius R = 1,0 · 10−5 m und der Dichte ̺ = 0,80 cmg 3 trägt die Ladung q = 1,0 · 10−13 C. (a) Welche maximale Ladung qmax könnte das Staubkorn tragen, wenn die elekV nicht überschreiten trische Feldstärke an seiner Oberfläche E0 = 1,0 · 107 m darf? (b) Das Staubkorn bewegt sich mit der Geschwindigkeit v1 = 10 ms senkrecht zu den Feldlinien des Erdmagnetfeldes (BErd = 4,8 · 10−5 T). Welchen Betrag F1 hat die Lorentzkraft auf das Teilchen? Vergleiche mit seiner Gewichtskraft! ~ (c) Das Staubkorn bewegt sich jetzt mit der Geschwindigkeit ~v im Feld B: 0 m ~v = 3 , s 4 1 ~ = 0 T B 4 Berechne die Lorentzkraft F~ auf das Teilchen. Wie groß ist F = |F~ |? Welchen Betrag a hat die Beschleunigung, die F~ dem Staubkorn verleiht? Wäre F~ die einzige Kraft auf das Teilchen, dann würde es eine Kreisbahn beschreiben. Welchen Radius r hätte diese Bahn? Lösung: (a) E0 = qmax 4πε0 R2 =⇒ qmax = 4πE0 ε0 R2 = 1,1 · 10−13 C (b) F1 = qv1 BE = 4,8 · 10−17 N, m = 4π 3 R ̺ = 3,4 · 10−12 kg 3 mg = 3,3 · 10−11 N = 6,8 · 105 F1 ~e1 ~e1 ~e1 12 12 mT ~ = q 0 3 4 = q 4 4 · 10−13 N (c) F~ = q~v × B = s 1 0 4 −3 −3 p F = 122 + 42 + 32 · 10−13 N = 1,3 · 10−12 N a= F m v2 = 0,39 2 = m s r =⇒ r= v2 = 64 m a 2