Zählen mit Baumdiagrammen und Zählprinzip
Werbung
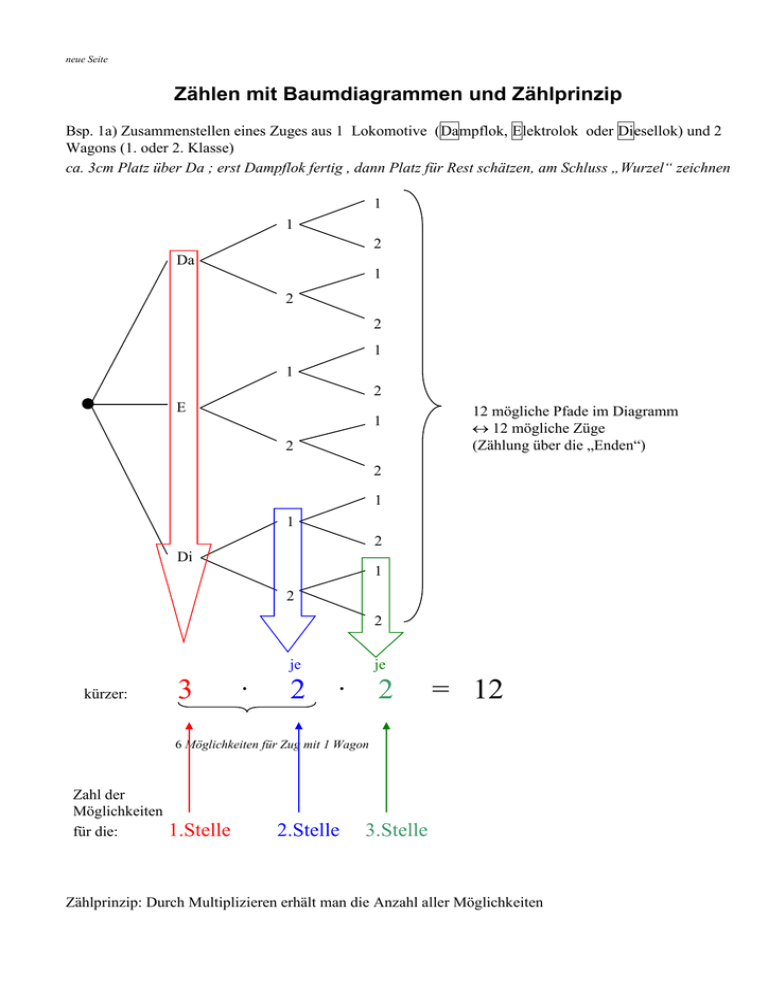
neue Seite Zählen mit Baumdiagrammen und Zählprinzip Bsp. 1a) Zusammenstellen eines Zuges aus 1 Lokomotive (Dampflok, Elektrolok oder Diesellok) und 2 Wagons (1. oder 2. Klasse) ca. 3cm Platz über Da ; erst Dampflok fertig , dann Platz für Rest schätzen, am Schluss „Wurzel“ zeichnen 1 1 2 Da 1 2 2 1 1 2 E 1 2 12 mögliche Pfade im Diagramm 12 mögliche Züge (Zählung über die „Enden“) 2 1 1 2 Di 1 2 2 je kürzer: 3 · 2 je · 2 = 12 6 Möglichkeiten für Zug mit 1 Wagon Zahl der Möglichkeiten für die: 1.Stelle 2.Stelle 3.Stelle Zählprinzip: Durch Multiplizieren erhält man die Anzahl aller Möglichkeiten 66 kW 1b) LS/ S. 126 Nr. 9) 74 kW w 92 kW 66 kW C 74 kW r 92 kW w ...................... Wenn es für jede Stelle jeweils gleich viele Möglichkeiten gibt (unabhängig von den vorherigen Stellen) , dann kann man sich mit dem Zählprinzip das Baumdiagramm sparen! GL r ...................... GLS ..................... je 3 · 2 je · 2 = 18 A.: ...... 0 HA : S.125 / Nr. 6 ) (Baum + Zählprinzip für a) ; b ohne Baum möglich) .1 . . . . 1c) zweistellige natürliche Zahlen : 1 9 . . . . . 2 . . . . . 9 . 0 1 . . . . 9 9 A.: Es gibt 90 zweistellige Zahlen · 10 = 90 1d) Anzahl der geraden vierstelligen Zahlen : 9 · 10 · 10 · 5 = 4500 An der letzten Stelle jeweils nur die Ziffern 0, 2, 4, 6 und 8 möglich! 1e) Anzahl der durch 5 teilbaren 8 stelligen Zahlen : 9 · 106 · 2 = 18 · 106 S. 126 / Nr. 8) Hinweis : Straßenwechsel bei jeder Stadt beliebig möglich (schlecht gezeichnet) evtl. Nr. 3) 2a) Ein 3 Steine hoher Turm soll aus gelben, roten und blauen Steinen gebaut werden (Vorrat „unbegrenzt“) Anzahl aller Möglichkeiten : 3 · 3 · 3 = 33 = 27 Baum nur an die Tafel und dann für Bsp. 3a) abändern ! 2b) 10 Steine hoher Turm / unbegrenzt viele rote und blaue Steine als Vorrat Zahl aller Mögl. : 210 = 1024 2c) Anzahl aller möglichen „bytes“ = = „Maschinenzeichen“-verschlüsselt durch 8-stellige Dualzahlen = 28 = 256 Wenn es für alle Stellen jeweils die gleiche Anzahl von Möglichkeiten gibt, dann ist die Zahl aller Möglichkeiten eine Potenz (Zahl der jeweiligen Möglichkeiten als Basis und Zahl der Stellen als Exponent) Anzahl aller 10-stelligen Zahlen im Zweiersystem = 1·29 = 512 Auch Morsezeichen werden nur mit 2 „Ziffer“-Zeichen verschlüsselt (kurz – lang bzw. Strich-Punkt) HA : S.126 / Nr. 10) HA : S. 126 / Nr. 13a) (b) ist sehr kompliziert : höchstens Knobelaufgabe 3a) 3 Steine hoher Turm aus begrenztem Vorrat : 1 gelber , 1 blauer und 1 roter Stein b r r b g r g b bzw. 6 „Enden“ r g g b b g r Zahl aller Mögl.: 3 · 1.Stein(unten) 2 2.Stein · 1 = 6 3.Stein 3b) wie 3a) , aber noch ein grüner und ein schwarzer Stein: 5 · 4 · 3 = 60 Mögl. 3c) ebenso, aber 5 Steine hoch : 5 · 4 · 3 · 2 · 1 = 120 Mögl. 3d) zehnstellige Zahlen mit lauter verschiedenen Ziffern : 9 · 9 · 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = ( 9 · 9!) = 3 265 920 Mögl. Abkürzung : 9! = 9 Fakultät (vgl. LS : S.99) Taschenrechner /Computer An 1.Stelle keine 0! jetzt noch 8 Ziffern übrig und die 0 ! a) aus den Ziffern 2,3,6,7,8 5·4· 3 = 60 b) mit lauter verschiedenen Ziffern : 9·9·8 = 81 · 8 = 648 Mögl. LZK : 3stellige Zahl Bei einem begrenzten Vorrat , bei dem nichts doppelt vorkommt, ist die Anzahl aller Möglichkeiten durch die „Fakultät“ gegeben, wenn der ganze Vorrat aufgebraucht wird und sonst keine Einschränkungen vorliegen (wie in 3d) HA : S. 125 / Nr. 4) 4a) 3 Steine hoher Turm aus folgendem Vorrat : 1 gelber, 3 blaue und 1 roter Stein b g r g b b r g r b b 1 r 2 b b r g b r g b 3 4 5 6 7 8 9 10 b 11 g 12 b 13 Vorsicht : Das Zählprinzip ist hier nicht anwendbar ( verschieden viele Mögl. für die 2. und 3.Stelle) Baumdiagramm nötig ! Unregelmäßiger Baum Zählen der Möglichkeiten über die Enden der Pfade : A.: Es gibt 13 Möglichkeiten weiteres Bsp.: LS / S.125 Bsp.1) ! HA : LS/ S. 125 / Nr. 5) S. 126 / Nr. 11) als Gegensatz : hier Vorrat praktisch unbegrenzt : a) 23 = 8 b) 33 = 27 LZK : bei 4 bzw. 5 Farben (je 3 Folien )? 43 = 64 Mögl. bzw. 53 = 125 Mögl. LS / S. 125/Nr. 7) als Gruppenarbeit : r r g g r g g r r g g r r r g r g g A.: Es gibt 6 Möglichkeiten g S. 126 / Nr. 12 ) Vorrat : 1 x rot ; 2 x gelb ; 4 x schwarz a) Vorsicht : Bei den Farbkombinationen ist die Reihenfolge unwesentlich, z.B. ist rg und gr dieselbe Kombination ! (Striche gleichfarbig) A.: Es gibt nur 5 verschiedene Kombinationen: rg, rs, gg, gs ,ss r s r g (geht auch „direkt“: auch Baum hier nicht mehr so sinnvoll!) g s Baum nur an Tafel! b) 2 davon sind gleichfarbig r c) Spätestens beim 4. Socken hat sie 2 gleichfarbige, weil es nur 3 Farben gibt s g s zur Wh. und Vertiefung verschiedene Typen gemischt aus LS : S. 199 / Nr. 26 ) 4! = 24 S. 16 / Nr. 17a) 9·10·1 = 90 17b) 9·10·9 = 810 17c) 1·10·10 = 100 17d) 1·10·1 = 10 17f) 8·10·9 = 720 Nr. 13b) 26 = 64 13c) 34 = 81 evtl. mit Baum: Nr. 15c) 6 + 5 + 4 + 3 + 2 + 1 = 3· 7 = 21 (nur Mögl. für 2. Ziffer wichtig) S. 9 / 12b) 4! = 24 mit Baum : / Nr. 12a) 4 evtl. 12c) 10 LZK : Anzahl der „Wörter“ aus den Buchstaben abc bzw. aaaab bzw abcde