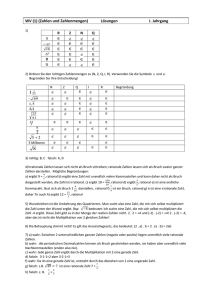
Kettenbruchentwicklung weiterer irrationaler Zahlen

Kettenbrüche
(Mathematik für Architekten, Winter 2004/05)
1. Ein gewöhnlicher Bruch wird zum Kettenbruch
2. Näherungsbrüche und wie sie berechnet werden
3. Eingabelung
4. Kettenbruchentwicklung für irrationale Zahlen
5. Beste Approximation
1. Ein gewöhnlicher Bruch wird zum Kettenbruch
757
169
 4 
 4 
81
169
1
169
81
 4 
1
2 
7
81
2 
1
 4 
2 
1
 4 
4
7
11 
11 
1
7
4
1
 4 
1
2 
1
2 
1
 4 
1
 4 
1
11 
1
81
7
1
2 
1
11 
1  3
4
1
1 1
4
3
1
 4 
1
2 
1
11 
1 
1
1
Man schreibt dafür
1
3
757
169

4, 2, 11, 1, 1, 3
Beachten Sie, wo die Teilnenner 2, 11, 1, 1, 3 im ausgeschriebenen Doppelbruch
vorkommen.
–2–
Kettenbruch-Algorithmus1
757
169

757 
81
 Rest = 4 

169 

169
169
81

169 
7
 Rest = 2 

 81 

81
81
7

81 
4
 Rest = 11 +

 7 

7
7
4

7 
3
 Rest = 1 +

4 

4
4
3

4 
1
 Rest = 1 +

3 

3
3
1

3 
 Rest = 3  0

1 

Der Kettenbruch-Algorithmus ist ein effizientes Verfahren zur Bestimmung der
Teilnenner.
Beachten Sie, wo hier die Teilnenner auftreten.
1
Unter  a  versteht man den ganzen Teil der (reellen) Zahl a. Das ist die grösste ganze Zahl, welche kleiner
oder gleich a ist.
–3–
Näherungsbrüche …
2.
 4,
4
4, 2
4, 2, 11
4, 2, 11, 1
 4
1
,
2
1
 4
,
1
2 
11
1
 4 
,
1
2 
1
1
11 
4, 2, 11, 1, 1
1
 4 
,
1
2 
1
11 
1
4, 2, 11, 1, 1, 3
1
1
1
 4 
,
1
2 
1
11 
1 
1
1
1
3
4, 2, 11, 1, 1, 3
sind die Näherungsbrüche des Kettenbruchs
… und wie sie (als gewöhnliche Brüche) berechnet werden
Nr.
0
1
2
3
4
5
Teilnenner
4
2
11
1
1
3
Zähler
Nenner
–4–
Oder : komfortabler (stets nach demselben Schema)
–2
–1
0
1
1
0
0
1
2
3
4
5
4
2
11
1
1
3
Und hier die abstrakten Formeln:
Der Kettenbruch a0 , a1, a2 , , a n und seine Näherungsbrüche a0 , a1 , a2 , , ak
(0  k  n) können wie folgt durch gewöhnliche Brüche ausgedrückt werden:
Für k  n definiere man ganze Zahlen p k , q k rekursiv durch
(a)
p 0  a 0 , p1  a1 a0  1, p k 1  a k 1 pk  p k 1 (2  k  n)
(b) q 0  1,
q1  a1 ,
q k 1  ak 1 q k  q k 1 (2  k  n)
Für den kten Näherungsbruch gilt dann
p
a0 , a1 , a2 , , a k  k für alle k (0  k  n) .
qk
3. Eingabelung
Die Näherungsbrüche
0
1
2
3
4
5
4
2
11
1
1
3
4
9
103
112
215
757
1
2
23
25
48
169
werden der Grösse nach geordnet:
4
103
215
757
112
9





1
23
48
169
25
2
Der gegebene Bruch wird durch die Näherungsbrüche sukzessive eingegabelt!
–5–
4. Kettenbruch-Entwicklung für irrationale Zahlen
Der Kettenbruch-Algorithmus wird hier auf die Irrationalzahl
3

 3
Rest = 1 
 3  1;
 3  1 
 3  1 

  Rest = 1  
 ;
 2 
 2 
3 1 
 3  1 
3 1

2
 3  1 
 3  1 

  Rest = 1  

 2 
 2 
Die Kettenbruchentwicklung von
3 1
2
1

3 1
3 1 
2
Rest = 2 +
3 angewendet.
2
3 1

3 1
 3  1
3 ist somit
3

usw.
1, 1, 2, 1, 2, 1, 2, 1, 2, 
Sie ist nicht abbrechend und periodisch. Man schreibt dafür:
3 
1, 1,2
Kettenbruchentwicklung weiterer irrationaler Zahlen
Eulersche Zahl
e 
2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 
Kreiszahl
  3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 
Goldener Schnitt
  1, 1, 1, 1, 1, 1, 1, 1, 1, 1,  
–6–
1
Wie bei den rationalen Zahlen können aus der Kettenbruch-Entwicklung ebenfalls
Näherungsbrüche bestimmt werden.
Näherungsbrüche von 3
–2
–1
0
1
1
0
0
1
2
3
4
5
6
7
8
9
1
1
2
1
2
1
2
1
2
1
1
 3
2
5 1
2
Näherungsbrüche von  
–2
–1
0
1
1
0
0
1
2
3
4
5
6
7
8
9
1
1
1
1
1
1
1
1
1
1
1
 
Beachten Sie Zähler und Nenner der Näherungsbrüche von  
Welche allgemeine Formel gilt für den nten Näherungsbruch?
–7–
2
5 1
.
2
Lösungen zur vorhergehenden Seite
Näherungsbrüche von 3
–2
–1
0
1
2
3
4
5
6
7
8
9
1
1
2
1
2
1
2
1
2
1
0
1
1
2
5
7
19
26
71
97
265
362
1
0
1
1
3
4
11
15
41
56
153
209
1 
5
19
71
265



 
3
11
41
153
3  
362
97
26
7



 2
209
56
15
4
5 1
2
Näherungsbrüche von  
–2
–1
0
1
2
3
4
5
6
7
8
9
1
1
1
1
1
1
1
1
1
1
0
1
1
2
3
5
8
13
21
34
55
89
1
0
1
1
2
3
5
8
13
21
34
55
1 
3
8
21
55
89
34
13
5



     



 2
2
5
13
34
55
21
8
3
Für den nten Näherungsbruch
pn
von  
qn
p
f
5 1
gilt n  n 2 .
qn
f n1
2
Dabei bezeichnet f n die nte Fibonacci-Zahl.
–8–
5. Beste Approximation
Für jede irrationale Zahl x gilt
x
(Dabei bezeichnet
pn
1
 2
qn
qn
für alle n.
pn
den n-ten Näherungsbruch der Zahl x.)
qn

Der n-te Näherungsbruch ist also stets eine gute rationale Approximation für x .
Diese Approximation ist sogar die bestmögliche, und zwar im folgenden Sinn:
Ist p q eine von p n q n (für ein n  1) verschiedene rationale Approximation der Zahl x
mit der Eigenschaft, dass qn  q  0 , so ist p n q n die bessere Approximation als p q :
x
pn
qn

x
p
q
(Beste Approximation erster Art)
Diese Eigenschaft der besten Approximation gilt offensichtlich auch für die Näherungsbrüche rationaler Zahlen.
Es ist genau diese Eigenschaft, welche die Kettenbrüche für Anwendungen interessant macht.
Es kommt in der Praxis nicht selten vor, dass eine rationale Zahl mit grossem Nenner durch
eine solche mit wesentlich kleinerem Nenner approximiert werden soll (z.B. Zahnräder).
–9–