Die Statistik (auf griechisch Stochastik)
Werbung
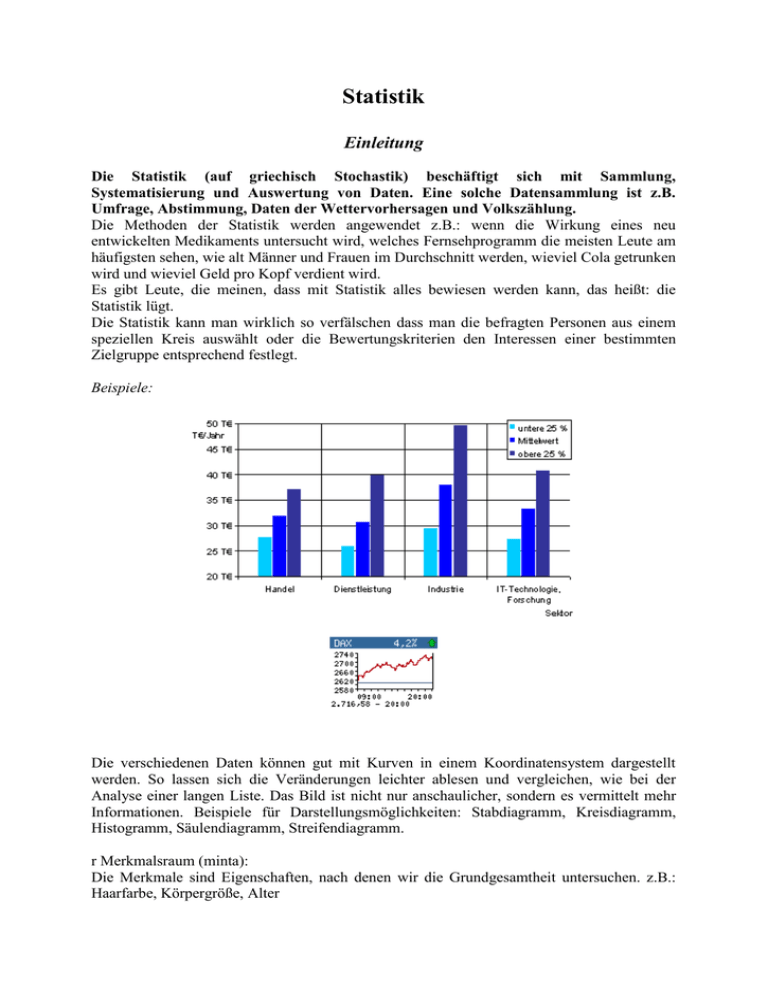
Statistik Einleitung Die Statistik (auf griechisch Stochastik) beschäftigt sich mit Sammlung, Systematisierung und Auswertung von Daten. Eine solche Datensammlung ist z.B. Umfrage, Abstimmung, Daten der Wettervorhersagen und Volkszählung. Die Methoden der Statistik werden angewendet z.B.: wenn die Wirkung eines neu entwickelten Medikaments untersucht wird, welches Fernsehprogramm die meisten Leute am häufigsten sehen, wie alt Männer und Frauen im Durchschnitt werden, wieviel Cola getrunken wird und wieviel Geld pro Kopf verdient wird. Es gibt Leute, die meinen, dass mit Statistik alles bewiesen werden kann, das heißt: die Statistik lügt. Die Statistik kann man wirklich so verfälschen dass man die befragten Personen aus einem speziellen Kreis auswählt oder die Bewertungskriterien den Interessen einer bestimmten Zielgruppe entsprechend festlegt. Beispiele: Die verschiedenen Daten können gut mit Kurven in einem Koordinatensystem dargestellt werden. So lassen sich die Veränderungen leichter ablesen und vergleichen, wie bei der Analyse einer langen Liste. Das Bild ist nicht nur anschaulicher, sondern es vermittelt mehr Informationen. Beispiele für Darstellungsmöglichkeiten: Stabdiagramm, Kreisdiagramm, Histogramm, Säulendiagramm, Streifendiagramm. r Merkmalsraum (minta): Die Merkmale sind Eigenschaften, nach denen wir die Grundgesamtheit untersuchen. z.B.: Haarfarbe, Körpergröße, Alter Die absolute Häufigkeit eines Variablenwertes gibt an, wie oft dieser Wert in der Liste vorkommt. Die relative Häufigkeit berechnet man nach der Formel: relativeHäufigkeit absoluteHä ufigkeit AnzahlderE lementederListe In der Tabelle ist das Ergebnis einer Umfrage nach den Sprachkenntnissen unter den Ungarn über 14 dargestellt: Sprachkenntnisse Anzahl der Personen 0: keine Sprachkenntnisse 5 603T 1: eine Fremdsprache 1 483T 2: zwei Fremdsprachen 906T 3: drei oder mehr Fremdsprachen 247T 6000 5000 4000 3000 2000 keine Sk 1 Fs. 2 Fs. 3 Fs. 1000 0 Man kann die Daten im Verhältnis zur Gesamtzahl der Bevölkerung über 14 angeben. Wenn wir berechnen, welcher Teil (wieviel Personen) der Einwohner 0, 1, 2, 3 oder mehr Fremdsprachen beherrscht, dann erhält man die relative Häufigkeit der Daten. So kann man die Daten in einem Histogramm darstellen und besser vergleichen. Beispiel: Möchte man herausfinden, wie häufig die Automarken A, B, C, D, E, F auf unseren Straßen anzutreffen sind, dann zählt man z.B. an einer bestimmten Straßenkreuzung eine Zeit lang die Autos der verschiedenen Marken. Aus den absoluten Häufigkeiten lassen sich dann die relativen Häufigkeiten berechnen. (Schüler Duden Seite 404. Tabelle) Quantitative Variablen: Variablen deren Werte reelle Zahlen sind. Qualitative Variablen: Variablen, die eine Eigenschaft ausdrücken z.B.: Haarfarbe Stichprobe: Eine Teilmenge der Grundgesamtheit, die durch ein Zufallsverfahren ausgewählt wird. Mittelwert: x ( arithmetisches Mittel / Durchschnitt): n xi x1 x 2 ... x n i 1 x n n Modalwert (Modus): Das ist der Wert, der in der Stichprobe am häufigsten auftaucht. Median: Zenttralwert deer geordneter Liste, die Zahl, die in dedr Mitte der Liste steht. Spannweite: die Differenz zwischen den kleinsten und größten Zahlen. Beispiel Thomas und Stefan sind gute Weitspringer, aber nur einer von ihnen darf an einem Wettkampf teilnehmen. Wen wird der Sportlehrer nach einem Blick auf die erzielten Weiten schicken? Thomas: 4,18; 4,20; 4,24; 4,19; der Durchschnitt: x 4,20 Stefan: 3,88; 4,28; 4,11; 4,31; 4,42 der Durchschnitt: x 4,20 Die zwei Listen, die denselben Mittelwert haben, unterscheiden sich doch. Will man den Unterschied zahlenmäßig ausdrücken, so liegt das Nahe, den Mittelwert der Differenzen xi x zu bilden. Er ist aber stets 0, bringt also den Unterschied nicht zum Ausdruck. Dieser zeigt sich erst, wenn man alle Abweichungen positiv nimmt, so bildet man den Mittelwert. So bekommen wir die mittlere absolute Abweichung. Thomas xi xi x 1 2 3 4 5 4,18 4,20 4,24 4,19 4,19 4,2 -0,02 0 0,04 -0,01 -0,01 0 Stefan xi xi x 1 2 3 4 5 3,88 4,28 4,11 4,31 4,42 4,2 -0,32 0,08 -0,09 0,11 0,22 0 xi x 0,02 0 0,04 0,01 0,01 0,016 n xi x 0,32 0,08 0,09 0,11 0,22 0,164 n Mittlere Abweichung: 1 xi x n ist ein Maß dafür, wie stark die Zahlen einer Liste vom Mittelwert abweichen. Standard Abweichung (Streuung): Es seien 2 1 s xi x n Begriffe absolute Häufigkeit abszolút gyakoriság Abweichung (e) eltérés arithmetisches Mittel számtani közép Ausgang (r) kimenetel Baumdiagramm (s) fadiagram Bernoulli-Experiment Bernoulli- kísérlet beschreibende Statistik leíró statisztika beurteilende Statistik matematikai statisztika Daten (pl.) adatok Diagramm (s) diagram empirische Standardabweichung tapasztalati szórás Empirisches Gesetz der großen Zahlen nagy számok törvénye Ereignis (s) esemény Ereignisraum (r) eseménytér Ergebnis (s) kimenetel Erhebung (e) mintavétel Gegenereignis (s) ellentett esemény geometrisches Mittel mértani közép geordnete Liste rendezett lista gewogenes arithmetisches Mittel súlyozott számtani közép Grundgesamtheit (e) alapsokaság, statisztikai sokaság harmonisches Mittel harmonikus közép Histogramm (s) hisztogram Kastenschaubild (s) sodrófa diagram Kenngrößen der Liste statisztikai mutatók Klasse osztály Klassenbreite osztályszélesség Klasseneinteilung (e) osztályba sorolás Klassenmitte osztályközép Kreisdiagramm (s) kördiagram Laplace - Experiment Laplace-kísérlet Liste (e) lista Medianwert (r) medián mehrstufiges Zufallsexperiment Merkmal –e (s) ismérv Merkmalsraum Mittelwert (r) középérték mittlere Abweichung átlagos abszolút eltérés mittlere quadratische Abweichung átlagos négyzetes eltérés Modus (r), Modi (e) módusz Pfadregel (e) láncszabály Piktogramm (s) piktogram quadratisches Mittel négyzetes közép qualitative Variable minőségi változó quantitative Variable mennyiségi változó Quartil (s) kvartilis Quartilabstand relative Häufigkeit relatív gyakoriság Säulendiagramm (s) oszlopdiagram sich stabilisieren állandósul sicheres Ereignis biztos esemény Spannweite (e) terjedelem Stabdiagramm (s) botdiagram Standardabweichung (e) szórás Statisik (e) statisztika statistische Stichprobe statisztikai mintavétel Streumaß (s) szórás unmögliches Ereignis lehetetlen esemény Variable (e) változó Varianz (e) szórásnégyzet, átlagos négyzetes eltérés Verteilung (e) eloszlás Zufallsexperiment (s) véletlenszerű kísérlet Stichprobe mit/ohne Zurücklegung visszatevéses/ visszatevés nélküli mintavétel geometrische Verteilung geometriai eloszlás hypergeometrische Verteilung hipergeometrikus eloszlás diskrete Verteilung diszkrét eloszlás stetige Verteilung folytonos eloszlás Binomialverteilung binomiális eloszlás bedingte Verteilung feltételes valószínűség Satz der totalen (vollen) Wahrscheinlichkeit teljes valószínűség tétele Verteilungsfunktion eloszlásfüggvény Wahrscheinlichkeitsverteilung (e) valószínűségi eloszlás Erwartungswert (r) várható érték Streuung (e) szórás Normalverteilung (e) normális eloszlás Dichtefunktion sűrűségfüggvény Verteilungsfunktion eloszlásfüggvény Neue Abituraufgabensammlung II. 2576. In den ersten fünf runden der spanischen Fußballmeisterschaft gab es in 7 Spielen kein Tor, in 6 Spielen 1 Tor, in 15 Spielen 2 Tore, in 13 Spielen 3 Tore, in 5 Spieln 4 Tore, in 2 Spielen 5 Tore, in einem Spiel 6 Tore, und in einem Spiel 7 Tore. a/ Fertigen Sie dazu eine Tabelle an, zeichnen Sie ein Säulen- und ein Kreisdiagramm! a/ Bestimmen Sie das arithmetische Mittel, den Modus und den Median! 2584. Die Orangenproduktion der Mittelmeerländer war 1978 folgende: Land Spanien Italien Israel Marokko Ägypten restliche Länder Produktion /in Millionen Tonnen/ 2,5 1,96 1 0,78 0,78 1,5 a/ Berechnen Sie den Prozentualen Anteil jedes Landes, und stellen Sie das Ergebnis in einem Kreisdiagram dar! b/ In Italien entfielen 1 Million Tonnen Orangen auf Sizilien, und 0,65 Millionen auf Calabrien. Wie hoch ist der prozentuale Anteil von Sizilien bzw. von Calabrien bezogen auf die gesamte italienische Produktion? 2593. Die Temperatur eines kranken Kindes wurde alle 4 Stunden gemessen. Die folgende Tabelle zeigt das Ergebnis der Messungen eines Tages. Uhrzeit Temperatur (°C) 6 37,5 10 38,2 14 39,2 18 38,5 22 38,0 a/ Zeichnen Sie die Fieberkurve des Kindes! b/ Kann man aufgrund der Fieberkurve feststellen, wie hoch die Temperatur des Kindes um 12 Uhr tatsächlich war? 2605. Der Flächeninhalt der einzelnen Kontinente in km2: Europe Asien Arika Amerika Australien und Ozeanien Antarktis 10 500 000 44 900 000 30 300 000 39 800 000 8 800 000 13 300 000 a/ Stellen Sie die Daten in einem Kreis- und einem Säulendiagramm dar! b/ Berechnen Sie die Gesamtfläche der Erde bei einem Radius von 6 378 km! Geben Sie die Oberfläche des Meeres an! Fertigen Sie ein Kreisdiagramm an,in dem der 7. Kontinent die Wasserfläche ist! 3450. Was bedeutet es, wenn a/ die Spannweite einer Datenmenge 0 ist? b/ die Streuung 0 ist? Folgt das eine aus dem anderen? 3451. Ist der Bericht eines Geschäftes realistisch, wenn man liest, dass 4% der Produkte Ausschuss ist, 6% schlechte, 23% mittelmäßige, 33% gute und 42% ausgezeichnete Qualität hat? Was denken Sie darüber? 3452. Zwei landwirtschaftliche Betriebe Sonnenschein und Mondschein ernteten 8 bzw. 7 Tonnen Erdbeeren. Drei Geschäfte bestellten von ihnen Erdbeeren: Spar 5 Tonnen, CBA 6 Tonnen. a/ Wie viele Erdbeeren bestellte das Geschäft Perfekt insgesamt von den beiden Betrieben? b/ Geben Sie eine Möglichkeit der Verteilung der Erdbeeren der zwei landwirtschaftlichen Betriebe an die drei Geschäfte an, so dass alle Erdbeeren verkauft werden! (Rechnen Sie mit ganzen Zahlen!) Spar CBA Perfekt Sonnenschein Mondschein 3454. Lassen Sie eine von den angegebenen Zahlen 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 weg, so dass der Durchschnitt der restlichen Zahlen 5 ergibt! Welche Zahl muss man weglassen? 3455. Eine Klasse erreichte in einer Klassenarbeit 10-mal die Note 3, je 2-mal die Note 1 und 5 und je 6-mal die Note 2 und 4. Ein Schüler bat den Lehrer, die Note nicht einzutragen, weil er während der Klassenarbeit Fieber hatte. Der Lehrer erfüllte die Bitte. So verbesserte sich der Durchschnitt um 0,08, Welche Note hätte der kranke Schüler bekommen? 3457. Kauft man eine 1 kg Bonbontüte, so muss man mit einer Abweichung von 50 g rechnen, bei einer 200 g Tüte mit 10 g. a/ Wo ist die Abweichung größer? b/ Wie würden Sie diese Abweichung (in Prozent) auf der Verpackung angeben? 3458. Der Blutdruck von 20 Menschen wurde gemessen, und man unterschied zwischen niedrigem (N), normalem (No) und hohem (H) Blutdruck. Man kam zu folgendem Ergebnis: H, H, No, H, H, No, N, N, No, No, No, No, H, H, No, No, H, H, N, No. Stellen Sie die relative Häufigkeit in einem Diagramm dar und bewerten Sie das Ergebnis! 3459. In der folgenden Tabelle ist der Kaloriengehalt einiger Früchte pro 100g reines Fruchtfleisch angegeben. Früchte Kaloriengehalt pro 100 g Apfel 30 Birne 50 Aprikose 46 Pfirsich 40 Walnuss 654 Haselnuss 691 Kastanie 167 Orange 40 Banane 103 a/ Wie groß ist die Spannweite der angegebenen Kalorienwerte? b/ Wie groß ist der prozentuale Unterschied der Frucht mit dem kleinsten Kaloriengehalt zur Frucht mit dem größten Kaloriengehalt in Bezug auf die Spannweite?