Hypothesentest Aufgabe 4 - klaus

R. Brinkmann http://brinkmann-du.de
Seite 1
08.06.2017
Hypothesentest Aufgabe 4
Der Hersteller eines Glücksspielautomaten behauptet, das die Wahrscheinlichkeit für
eine bestimmte Gewinnkombination p = 0,3 beträgt. In 170 Spielrunden soll diese
Angabe überprüft werden.
a) Geben Sie eine Entscheidungsregel für das Signifikanzniveau   10% an
und berechnen Sie den Fehler 1. Art. Skizzieren Sie grob die Verteilungsfunktion
und markieren Sie die markanten Werte.
Bemerkung: Der Annahmebereich soll symmetrisch zum Erwartungswert liegen.
b) Bestimmen Sie die Wahrscheinlichkeit für den Fehler 2. Art, falls die tatsächliche
Wahrscheinlichkeit dieser Gewinnkombination nur p = 0,2 beträgt. Skizzieren Sie
grob die Verteilungsfunktion und markieren Sie die markanten Werte
a) Nullhypothese : H0 : p0  0,3 Signifikanzniveau :   10%
Es handelt sich um einen zweiseitigen Hypothesentest.
Zu bestimmen ist eine 90%  Umgebung für   n  p 0  170  0,3  51
Es ist   n  p  1  p   51 0,7  35,7  5,975  3
Damit wird   1,64    51  1,64  5,975  41,2 und
  1,64    51  1,64  5,975  60,8
Annahmebereich :
A   41 ... 51 ...61 
Ablehnungsbereich : A   0... 40 
symmetrisch 
 62...170 
Es ist zu überprüfen, ob mindestens 90% der Testergebnisse
im Annahmebereich liegen.
P  41  X  61  P  40,5  X  61,5 
r  10,5 
r
10,5

 r  1,76    z  1,76  P  41  X  61  0,922  90%
 5,975
Gegenprobe : P  42  X  60   P  41,5  X  60,5 
r
9,5

 r  1,59    z  1,59  P  42  X  60   0,888  90%
 5,975
Damit bleibt der Annahmebereich unverändert.
Falls p0 = 0,3 richtig ist, aber das Stichprobenergebnis zufällig in den
Ablehnungsbereich fällt, geht man fälschlicherweise davon aus, dass H0
abgelehnt werden muss. Die Wahrscheinlichkeit für den Fehler 1. Art ist gleich
der Wahrscheinlichkeit für den Ablehnungsbereich, also 1 – 0,922 = 0,078 (7,8%).
r  9,5 
Erstellt von R. Brinkmann 747103324
17.01.2007 16:29:00
Seite 1 von 4
R. Brinkmann http://brinkmann-du.de
Seite 2
08.06.2017
n  170 p  0,3   51   5,975
Annahmebereich 92,2%
Fehler 1. Art
7,8%
40
62
51
b) Falls H0 nicht gilt, (d.h. die Hypothese p0 = 0,3 ist falsch), aber das
Stichprobenergebnis zufällig im Annahmebereich von H0 liegt, nimmt man H0
fälschlicherweise an. Die Wahrscheinlichkeit dafür, diesen Fehler zu machen
ist der Fehler 2. Art.
  P0,2  41  X  61
n  170
p  0,2   n  p  170  0,2  34
  n  p 1  p   34  0,8  27,2  5,215  3
[... { 7...27 } { 28...34... 40 } { 41...61} ...]
1
P  7  X  61  P  28  X  40  
2
P  7  X  61  P  6,5  X  61,5 
P  41  X  61 
r  27,5 
r
27,5

 r  5,27    z  5,27
 5,215
P  7  X  61  1
P  28  X  40   P  27,5  X  40,5 
r  6,5 
r
6,5

 r  1,25    z  1,25
 5,215
P  28  X  40   0,789
P  41  X  61 
1
1  0,789   0,106
2
Bemerkungen zum Test.
Bei diesem Test handelt es sich um einen zweiseitigen Hypothesentest.
Der Ablehnungsbereich liegt zu beiden Seiten des Annahmebereichs.
Der Fehler 2. Art kann nur dann berechnet werden, wenn die tatsächliche
Erfolgswahrscheinlichkeit ( p1 = 0,2 ) bekannt ist.
Erstellt von R. Brinkmann 747103324
17.01.2007 16:29:00
Seite 2 von 4
R. Brinkmann http://brinkmann-du.de
Seite 3
08.06.2017
Schlussbemerkung:
Falls H0 richtig ist, liegt das Ergebnis des Zufallsversuchs zu 92,2% im
Annahmebereich von H0. Irrtumswahrscheinlichkeit 7,8%.
Falls hingehen H0 falsch und p1 = 0,2 richtig ist, fällt das Ergebnis dennoch zu 10,6%
in den Annahmebereich von H0.
n  170 p  0,3   34   5,215
Fehler 2. Art
10,6%
Annahmebereich von H0
34
Erstellt von R. Brinkmann 747103324
41
17.01.2007 16:29:00
Seite 3 von 4
R. Brinkmann http://brinkmann-du.de
Seite 4
08.06.2017
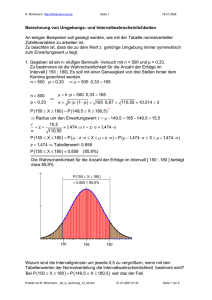
Gegenüberstellung der Verteilungen zur Veranschaulichung der Zusammenhänge.
n  170 p  0,3   51   5,975
Annahmebereich 92,2%
Fehler 1. Art
7,8%
40
51
62
n  170 p  0,3   34   5,215
Fehler 2. Art
10,6%
Annahmebereich von H0
34
Erstellt von R. Brinkmann 747103324
41
17.01.2007 16:29:00
Seite 4 von 4