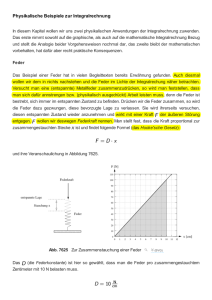
Document

Aufgabe 4: Kreisbewegungen
a.) Nehmen Sie an, dass sich ein Raumschiff auf einer Umlaufbahn 400km über der Erdoberfläche befindet und die Erde einmal in T = 90 Minuten umkreist. Ermitteln Sie die Zentripetalbeschleunigung des Raumschiffes auf seiner Umlaufbahn. Geben Sie die Antwort in
Einheiten g , der Fallbeschleunigung an der Erdoberfläche, an. Nehmen Sie als mittleren
Erdradius 6371km an.
b.) In der Raumfahrt wird die Erzeugung „künstlicher Schwerkraft“ mittels rotierender Raumschiffe diskutiert (Beispiel im Bild, aus dem Film
2001). Wie schnell muss sich ein so gestaltetes Raumschiff bei einem
angenommenen Durchmesser von 100m um die zentrale Achse drehen,
damit auf einen Körper in der kreisförmigen Struktur Beschleunigung
von 1 g existiert? Wie groß ist dabei die Bahngeschwindigkeit?
Zu a.)
v2
.
r
-
Für die Zentripetalbeschleunigung gilt a =
-
Als Bahngeschwindigkeit eines kompletten Umlaufs des Raumschiffes folgt v =
2π ⋅ r
.
T
4π 2 ⋅ r 2 4π 2 ⋅ r
v 2 (2π ⋅ r )
. Mit dem Radius r = 6371 + 400 = 6771 km
=
=
=
r
T 2r
T 2r
T2
m 9.17
4π 2 ⋅ 6771000 m
ergibt sich a =
g = 0.93g
= 9.17 2 =
2
2
s
9.81
(90 ⋅ 60) s
2
Damit folgt a =
Zu b.) Entsprechend der Darstellung in Aufgabenstellung a.) ergibt sich aus a =
Zusammenhang für die Umlaufzeit T 2 =
4π 2 ⋅ r
der
T2
4π 2 ⋅ r
r
⇔ T = 2π
. Nach Einsetzen erhalten wir
a
a
50
s = 14s als Zeit für eine komplette Rotation der Struktur. Für die Bahngeschwin9.81
2π ⋅ r 2π ⋅ 50m
m
km
digkeit folgt mit v =
=
= 22 = 81
.
T
14s
s
h
T = 2π
Aufgabe 5: Gravitation
Berechnen Sie den Wert der Fallbeschleunigungen g für die Planeten des Sonnensystems.
Beschränken Sie die Angabe auf signifikante Stellen.
Planetendaten:
Merkur
Masse [kg]
Mittlerer äquatorialer
Radius (m)
g (m/s2)
Venus
Mars
Jupiter
Saturn
Neptun
4,87 · 1024
6051590
6,42 · 1023
3397000
1,90 · 1027
71492680
5,69 · 1026
60267140
8,68 · 1025
25559000
1,02 · 1026
24764000
3.70
8.88
3.71
24.8
10.5
8.87
11.1
Die Fallbeschleunigung ergibt sich aus dem Gravitationsgesetz über g =
γ = 6.67428 ⋅10−11
Uranus
3,30 · 1023
2439764
M ⋅γ
, mit
r2
m3
. Die berechneten Werte sind in der Tabelle zusammengefasst.
kg s 2
Aufgabe 6: Integrieren mit zeitabhängiger Beschleunigung
Ein Versuchsfahrzeug startet vom Stillstand (v0 = 0 m s ) bei t = 0s und beschleunigt mit einer
(
)
angegebenen Beschleunigung von a = 7 . 00 m s 3 t . Wie groß ist (a) seine Geschwindigkeit und (b) sein Weg 2.00s später?
a.) Die Geschwindigkeit v ist unter Verwendung der Integralrechnung als Funktion von t zu
bestimmen. Aus der Definition der Beschleunigung a = dv dt ergibt sich
dv = a ⋅ dt .
Nun kann in der Gleichung auf beiden Seiten das bestimmte Integral gebildet werden, mit den
Grenzen v = 0 m s für t = 0s bis v bei einer beliebigen Zeit t . Es folgt
t
t
m
m
m  t 2 



 
=
⋅
⇒
=
⋅
=
⋅
=
dv
a
dt
v
(
t
)
7
.
00
t
dt
7
.
00
t
dt
7
.
00


∫ ∫
∫  s3 
3 ∫
3 

s
s




 2 0
0
0
0
0
v
t
t
 
m  t 2
m

=  7.00 3  − 0  =  3.50 3 t 2
s  2
s 

 
m
m

Bei t = 2s ergibt dieses eine Geschwindigkeit von v(t ) =  3.50 3 (2.00s )2 = 14.0 .
s
s 

b.) Analog kann der Weg x unter Verwendung der Integralrechnung und Berücksichtigung
von x0 = 0m für t = 0s bestimmt werden. Aus der Geschwindigkeit v = dx dt ergibt sich
dx = v ⋅ dt .
Nun kann in der Gleichung auf beiden Seiten das bestimmte Integral gebildet werden, mit den
Grenzen x = 0m für t = 0s bis x bei einer beliebigen Zeit t . Es folgt
x
t
t = 2.00s
0
0
0
∫ dx = ∫ v ⋅ dt ⇒ x(t ) = ∫
t = 2.00s
m 2
m  t 3 


 3.50 3 t ⋅ dt =  3.50 3  
s 
s  3  0


= 9.33m
Aufgabe 7: Reibungskraft im freien Fall
Bestimmen Sie die Geschwindigkeit in Abhängigkeit der Zeit für einen Körper, der aus der
Ruhelage frei fällt, wenn eine Widerstandskraft vorhanden ist, die linear proportional zur Geschwindigkeit v ist.
Im freien Fall wirken zwei Kräfte auf den Körper, einerseits die Gewichtskraft
FG = mg
sowie die entgegengesetzt wirkende Reibungskraft
FR = −bv .
Hierbei ist b der Luftreibungsparameter. Somit kann die resultierende Kraft über das 2. Newtonsche Axiom beschrieben werden als
dv
Fgesamt = ma = m = FG + FR = mg − bv
dt
b
dv
⇒
=g− v
m
dt
Letztlich soll die Geschwindigkeit als Funktion bestimmt werden, die letzte Gleichung wird
also zum Integrieren umgestellt:
dv
dv
b
dv
b
= dt ⇔
= dt ⇔
= − dt .
b
m
m
m
g− v
g −v m
v− g
m
b
b
Dieser Ausdruck kann integriert werden:
v
t
v
v
−1
t
b
m 
dv
dv
b

∫ m = ∫ − m dt ⇔ ∫ m = ∫  v − b g  dv = − m ∫ dt
0 v−
0 v−
0
g 0
g 0
b
b
v
t
 v − mg b 
b
b
b
 m 
 m 
m 
⇒ ln v − g  = ln v − g  − ln  g  = − t = − t ⇒ ln 
=− t

m
m
m 0
b 
b 0


b 
 − mg b 
Unter Nutzung der Umkehrfunktion des natürlichen Logarithmus kann geschrieben werden
  v − mg b   v − mg b
 b 
exp ln 
= exp − t 
=

 m 
  − mg b   − mg b
.
mg
mg
mg 
 b 
 b 
exp − t  ⇒ v =
1 − exp − t  
⇒v−
=−
b
b
b 
 m 
 m 
Aus der Gleichung ist zu entnehmen, dass nach hinreichend langer Zeit eine stationäre Endgemg
vom Gewicht des Körpers sowie
schwindigkeit erreicht wird, welche über v(t → ∞ ) =
b
dem Reibungskoeffizienten b abhängt. Dieses ist die Grundlage des Fallschirmspringens