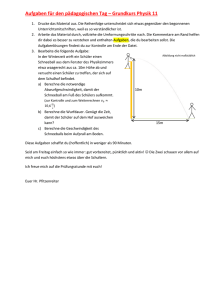
Der schiefe Wurf
Werbung
Der schiefe Wurf
Walter Fendt
10. April 2003
Ein Körper der Masse wird in der Höhe über dem Boden mit der Anfangsge
schwindigkeit geworfen, und zwar unter dem Winkel gegenüber der Waagrechten. Die Bewegung des Körpers wird beein¤usst von der Gewichtskraft – entsprechend der Fallbeschleunigung . Die Luftwiderstandskraft soll vernachlässigt
werden.
1 Koordinaten
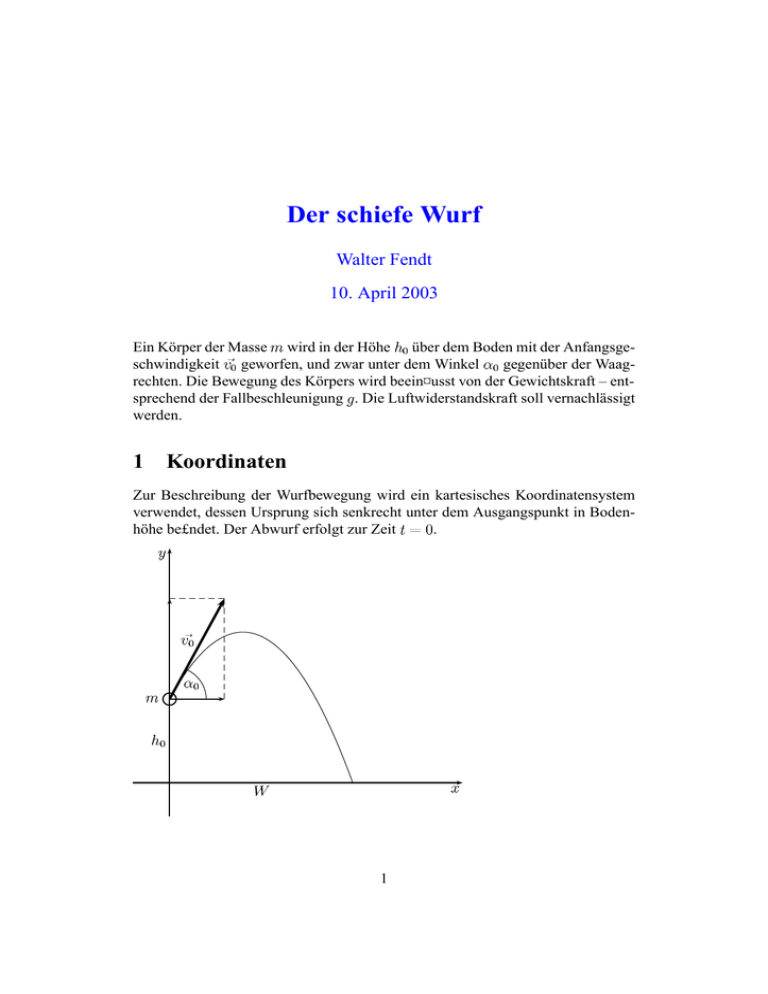
Zur Beschreibung der Wurfbewegung wird ein kartesisches Koordinatensystem
verwendet, dessen Ursprung sich senkrecht unter dem Ausgangspunkt in Bodenhöhe be£ndet. Der Abwurf erfolgt zur Zeit .
1
In den Berechnungen werden folgende Größen verwendet:
!
"
"
#
#
$&% ' (
$
) * +
$
Ortsvektor
waagrechte Koordinate
senkrechte Koordinate
Zeit
Fallbeschleunigung
Anfangsgeschwindigkeit (Vektor)
Anfangsgeschwindigkeit (Betrag)
Abwurfwinkel (gegenüber der Waagrechten)
Ausgangshöhe
Wurfdauer
Wurfweite
maximale Höhe über dem Boden
Geschwindigkeit (Vektor)
Geschwindigkeit (Betrag)
waagrechte Geschwindigkeitskomponente
senkrechte Geschwindigkeitskomponente
Winkel der Bewegungsrichtung gegenüber der Waagrechten
Masse
Beschleunigung (Vektor)
Beschleunigung (Betrag)
Kraft (Vektor)
Kraft (Betrag)
kinetische Energie (Bewegungsenergie)
potenzielle Energie (Lageenergie)
Gesamtenergie
In waagrechter Richtung ( -Richtung) bewegt sich der Körper mit der konstanten
Geschwindigkeit -, .0/ :
-Koordinate:
213 , .0/ (1)
In senkrechter Richtung ( -Richtung)
erfolgt eine gleichförmig beschleunigte Be
wegung. Die Ausgangshöhe ist , die Anfangsgeschwindigkeit in -Richtung
beträgt -/ 4 5 (bei positivem nach oben, also in positive -Richtung gerichtet). Da die (Fall-)Beschleunigung den Betrag hat und nach unten gerichtet ist
(in negative -Richtung), muss für die Beschleunigung in -Richtung der Wert 6 eingesetzt werden.
2
7 -Koordinate:
798;:<>=@? < AB C D&EF<HGJIK-A L
(2)
Als nächstes soll die Gleichung der Wurfbahn aufgestellt werden. Man löst dazu
(1) nach A auf und setzt das Ergebnis in (2) ein:
AM8
N
? <-O P Q
B E <
798;:<>=@? <HRSN
R B C D&EF<HGJIKUTVN
? <-O P BE <
? <-O P BQE < W
L
8;: < =
D&E < G K I0N
N&X Y
? <L O P B L E <
L
Gleichung der Wurfbahn:
798ZG K
I
L =J[ D\E < ] =^: <
? <L O P B L E < N
XY
N
(3)
Aus dieser Gleichung ist zu erkennen, dass die Wurfbahn Teil einer nach unten
geöffneten Parabel ist.
Um die Dauer _ des Wurfs zu bestimmen, setzt man in Gleichung (2) die Höhe 7
gleich 0:
: < =@? < _ B C D&E < GJIK _ L 83`ba R
K
K
G _ L= ?c< _ B C D&EF<>= :Q<d83`
I
K
Verwendung der bekannten Lösungsformel für quadratische Gleichungen ergibt:
K
K
? < B C D&E <
egf [ ? < B C D\E < ] L GihjRk[ G ] R : <
I
K
Rk[ G ]
I
K
G ? <-B C D&EF< e f h0? < L B C D L EF<>=^l :Q<
I
K
G
I
K
?c<-B C D&EF<
m f ? < L B C D L EF<=
:<
I
I
G
8
_
8
8
K
3
Das Minuszeichen vor der Wurzel würde zu einem negativen Wert von n führen.
Daher muss das Pluszeichen richtig sein.
Wurfdauer:
nboqp r-s t u&vFr>wgx pkr y s t u y vFr>w^z {k|r
{
(4)
Durch Einsetzen dieses Ergebnisses in Gleichung (1) erhält man nun problemlos
die Wurfweite:
}
o
p r-~ sQv r
n
Wurfweite:
}
p r ~ sQvFrHcpcr-s t u&vFr>w x p r y s t u y vFr>w^z {k|r
o
(5)
{
Als nächstes soll die maximale Höhe errechnet werden. Dazu ist die zeitliche
Ableitung von (2) gleich 0 zu setzen.
o3
pcr-s t u&vFrHi{0
o
p r s t u&v r
{
Dieser Wert für (der Zeitpunkt der maximalen Höhe) kann nun in (2) eingesetzt
werden.
o
p r s t u&v r
{
s t u\vFrH
{
z
p r y s t u y vFr
p r y s t u y vFr
| r w
{
z {
|r>w@pcr
|
o
4
p r s t u\v r y
{S
Maximale Höhe über dem Boden:
Q
;>k
(6)
2 Geschwindigkeit
Die beiden Komponenten der Geschwindigkeit, (waagrecht) und (senkrecht)
erhält man durch Differenziation von (1) beziehungsweise (2) nach der Zeit .
Waagrechte Komponente der Geschwindigkeit:
-
(7)
Senkrechte Komponente der Geschwindigkeit:
H
(8)
Der Geschwindigkeitsbetrag ergibt sich nun aus dem Satz des Pythagoras:
Z
¡
¡
£
Q
¢ J¡
H
Q
¢ ¦
¤¥
§-¨
¢
>
Betrag der Geschwindigkeit:
ª©
>
5
(9)
Kombiniert man die Beziehungen (7) und (8) miteinander, so erhält man den Winkel « , den die momentane Bewegungsrichtung mit der Waagrechten einschließt:
¬­ ®
«°¯q± ²
± ³
Winkel zwischen Bewegungsrichtung und Waagrechter:
¬­ ®
®
«
«°¯q± ´-µ ¶ H
´ ·i¸0¹
«
± ´-º » µ ´
(10)
3 Beschleunigung
Über die Beschleunigung gibt es nicht viel zu sagen. Der Beschleunigungsvektor
hat zu jedem Zeitpunkt den Betrag (Fallbeschleunigung) und ist nach unten
¸
gerichtet. Man beachte, dass die Richtung des Beschleunigungsvektors nicht mit
der Bewegungsrichtung übereinstimmt!
4 Kraft
Nach dem zweiten Newtonschen Axiom (Kraftgesetz) besteht zwischen der Be¾
¾
schleunigung ½ ¼ und der Kraft ¼ der Zusammenhang ¼ ¯À¿@½ ¼ , wobei ¿ für die
¾
Masse steht. Bei der Kraft ¼ , die demnach den Betrag ¿
hat, handelt es sich
¸
natürlich um die Gewichtskraft (Gravitationskraft). Der Kraftvektor ist wie der
Beschleunigungsvektor nach unten gerichtet.
5 Energie
Die kinetische Energie (Bewegungsenergie) ergibt sich aus Á&Â Ã ÄU¯
(9) den Wert von liefert.
¿Å
±kÆ
, wobei
±
Kinetische Energie:
Á& à Äǯ
¿ ÅJÈ
Å
± ´ ¸0¹µ ¶
±k´ Æ ·
6
®
«
´>É ¸kÆ ¹ Æ Ê
(11)
Die potenzielle Energie (Lageenergie, hier genauer: Höhenenergie) sei so festgelegt, dass sie am Boden den Wert 0 hat. Es gilt Ë
Ì Í Î-ÏÐUÑ0Ò und somit gemäß (2):
Potenzielle Energie:
Ë ÌÍÎ
ÏbÐUÑÔÓkÕÖ>×@Ø Ö ÙÚ Û Ü&ÝFÖHÞ
Ñß
Ùàá
(12)
Damit lässt sich die Gesamtenergie angeben:
Ë;Ï;Ë&â ã ä&×^Ë
Ì ß Í Î
Ñß
Ð ßJå
Ï
Ø Ö à Þ Ø Ö Ñ0ÙÚ Û Ü&Ý Ö @
× Ñ àÙàæ @
× ÐUÑ Ó Õ Ö ×@Ø Ö ÙÚ Û Ü&Ý Ö Þ
Ùàá
Ðß
Ðß
Ðß
Ï
Ø Ö à ÞiÐUØ Ö Ñ0ÙÚ Û Ü\Ý Ö ×
Ñ àÙà @
× ÐUÑkÕ Ö ×@ÐUÑ0Ø Ö ÙÚ Û Ü&Ý Ö Þ
Ñ àÙà
Ðß
Ï
Ø Ö à ×^ÐçÑkÕ Ö
Dieser Ausdruck hängt – in Übereinstimmung mit dem Energieerhaltungssatz –
nicht von der Zeit Ù ab.
Gesamtenergie:
ËèÏ
Ðß
Ø Ö à ×@ÐUÑkÕ Ö
é
c Walter Fendt, http://www.walter-fendt.de/phys/mech/wurf.pdf
Letzte Änderung am 13. April 2003
7
(13)