Aufgaben für den pädagogischen Tag – Grundkurs Physik 11

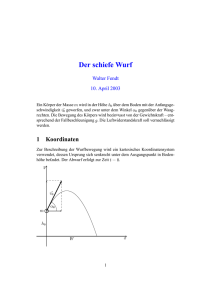
Aufgaben für den pädagogischen Tag – Grundkurs Physik 11
1. Drucke das Material aus. Die Reihenfolge unterscheidet sich etwas gegenüber den begonnenen
Unterrichtsmitschriften, weil es so verständlicher ist.
2. Arbeite das Material durch, vollziehe die Umformungsschritte nach. Die Kommentare am Rand helfen
dir dabei es besser zu verstehen und enthalten Aufgaben, die du bearbeiten sollst. Die
Aufgabenlösungen findest du zur Kontrolle am Ende der Datei.
3. Bearbeite die folgende Aufgabe:
Abbildung nicht maßstäblich
In der Winterzeit wirft ein Schüler einen
Schneeball aus dem Fenster des Physikzimmers
etwa waagerecht aus ca. 10m Höhe ab und
versucht einen Schüler zu treffen, der sich auf
dem Schulhof befindet.
a) Berechne die notwendige
Abwurfgeschwindigkeit, damit der
10m
Schneeball am Fuß des Schülers aufkommt.
(zur Kontrolle und zum Weiterrechnen 𝑣0 ≈
m
10,6 )
s
b) Berechne die Wurfdauer. Genügt die Zeit,
damit der Schüler auf dem Hof ausweichen
kann?
c) Berechne die Geschwindigkeit des
Schneeballs beim Aufprall am Boden.
15m
Diese Aufgaben schaffst du (hoffentlich) in weniger als 90 Minuten.
Seid am Freitag einfach so wie immer: gut vorbereitet, pünktlich und aktiv!  Die Zwei schauen vor allem auf
mich und euch höchstens etwas über die Schultern.
Ich freue mich auf die Prüfungsstunde mit euch!
Euer Hr. Pfitzenreiter
Der waagerechte Wurf
y
𝑣0 ⊥ 𝑣𝑦 ⇒ unabhängige Überlagerung der Bewegungen
x
𝑣0
𝑣0
𝑣𝑦
in 𝑠𝑥 -Richtung gleichf. Bewegung
𝑣𝑥 (𝑡) = 𝑣𝑜 = konstant
in 𝑠𝑦 -Richtung gleichm. beschleunigte Bewegung
𝑣𝑦 (𝑡) = −𝑔 ⋅ 𝑡
𝑠𝑥 (𝑡) = 𝑣0 ⋅ 𝑡
𝑠𝑦 (𝑡) = − 2 𝑡 2
𝑔
Bahnkurve
…ist die Menge der Orte, an denen sich der Körper im Laufe seiner Bewegung befindet. Zur Beschreibung der
Bahnkurve wird ein Zusammenhang zwischen 𝑠𝑥 und 𝑠𝑦 gesucht, der die Zeit nicht enthält.
𝑠𝑥 = 𝑣0 ⋅ 𝑡 → 𝑡 =
𝑠𝑥
𝑣0
𝑔
𝑠𝑦 = − 2 𝑡 2
𝑔
2
𝑠
𝑠𝑦 = − 2 ⋅ (𝑣𝑥 )
0
𝑠𝑦 = −
𝑔
𝑠 2
2𝑣0 2 𝑥
Da 𝑠𝑦 ~ 𝑠𝑥 2 ergibt sich im 𝑠𝑥 -𝑠𝑦 -Diagramm eine Parabel, die auch Wurfparabel genannt wird.
Gesamtgeschwindigkeit
Wiederholung: Vektoraddition von Geschwindigkeiten, die senkrecht aufeinander stehen
→ die resultierende Endgeschwindigkeit ergibt sich als Diagonale des Rechtecks
→ die Bewegungsrichtung kann durch Konstruktion ermittelt werden
→ die Größe der Geschwindigkeit ergibt sich als Länge des Pfeils
Damit ergibt sich zur Berechnung der Gesamtgeschwindigkeit:
Wurfdauer 𝒕𝒘 und Wurfweite 𝒔𝒘 aus der Höhe ℎ
Für diese unabhängige Bewegungsüberlagerung erhält man die Wurfdauer 𝑡𝑤 wie beim
freien Fall:
𝑔
𝑠𝑦 = − 2 𝑡 2
umgestellt nach t
𝑡 = √−
2𝑠𝑦
𝑔
bei Wurfdauer 𝑡𝑤 ist 𝑠𝑦 = −ℎ
2ℎ
𝑡𝑤 = √ 𝑔
Die Wurfdauer ist nicht abhängig von der Anfangsgeschwindigkeit 𝑣0
und nicht abhängig von der Masse des Körpers.
Da unabhängige Überlagerung erhält man die Wurfweite 𝑠𝑤 als Weg, den der Körper in 𝑠𝑥 -Richtung nach der
Wurfdauer 𝑡𝑤 zurückgelegt hat:
𝑠𝑤 = 𝑠𝑥 (𝑡𝑤 ) = 𝑣0 ⋅ 𝑡𝑤
2ℎ
𝑠𝑤 = 𝑣0 ⋅ √
𝑔
m
s
Beispiel: 𝑣0 = 15 , 𝑔 = 10
m
s2
𝑡 in s
0
1
2
3
4
𝑠𝑥 in m
𝑠𝑦 in m
m
s
m
𝑣𝑦 in s
𝑣𝑥 in
𝑣𝑟𝑒𝑠 in
m
s
𝑠𝑦
𝑠𝑥
5
m
m
Lösungen für das Beispiel: 𝑣0 = 15 s , 𝑔 = 10 s2
𝑡 in s
0
1
2
3
4
5
𝑠𝑥 in m
0
15
30
45
60
75
𝑠𝑦 in m
0
−5
−20
−45
−80
−125
15
15
15
15
15
15
0
−10
−20
−30
−40
−50
15
18,0
25
33,5
42,7
52,2
m
𝑣𝑥 in s
m
𝑣𝑦 in s
𝑣𝑟𝑒𝑠 in
m
s
(Nichtgerundete ganze Zahlen werden ohne Nachkommastellen angegeben, obwohl es einer sinnvollen Genauigkeit entsprechen würde.)
𝑠𝑦
𝑠𝑥