Satz des Thales - Schulentwicklung NRW
Werbung

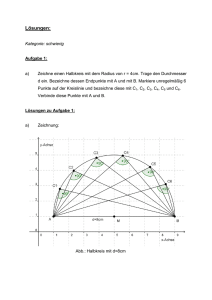
Variante A KPG Jgst. 9 Satz des Thales Erkundung GA 1/2 Vorbereitung Zeichnet auf den Hof mit Kreide eine Strecke ̅̅̅̅ 𝐴𝐵 der Länge 5 m mit dem Mittelpunkt M. Schlagt mithilfe eines Bindfadens von 2,50 m Länge einen Halbkreisbogen um den Mittelpunkt M, der durch die Punkte A und B verläuft. Markiert auf dem Halbkreisbogen einen beliebigen Punkt 𝐶. Die Thales-Figur Stellt drei Personen auf: Je eine an die Punkte 𝐴, 𝐵 und 𝐶. Schätzt mit ausgestreckten Armen die Größe der Winkel des Dreiecks. Wie verändern sich die Winkel, wenn die Person 𝐶 auf dem Halbkreisbogen wandert? Ergebnis Was fällt euch auf? Beschreibt eure Beobachtungen. Formuliert anschließend begründete Vermutungen. Document1 QUA-LiS.NRW Variante A KPG Jgst. 9 Satz des Thales Erkundung PA 2/2 Konstruktion Überprüft eure Vermutung vom Schulhof mit Hilfe eines DGS-Programms. Folgende Tipps können euch helfen: Öffnet ein Blatt in Eurem DGS-Programm und speichert es unter einem geeigneten Namen. ̅̅̅̅ und tragt den Mittelpunkt M ein. Zeichnet eine beliebige Strecke 𝐴𝐵 ̅̅̅̅̅. Zeichnet einen Halbkreis mit Mittelpunkt M und Radius 𝐴𝑀 Legt einen Punkt C fest: er soll auf dem Halbkreis liegen, dort aber beweglich sein. ̅̅̅̅ und 𝐵𝐶 ̅̅̅̅ . Zeichnet die Strecken 𝐴𝐶 Messt die drei entstandenen Winkel des Dreiecks ABC und notiert die Werte in einer geeigneten Tabelle. Bewegt C auf dem Halbkreis und messt jedes Mal die neu entstandenen Innenwinkel des Dreiecks. α β γ Ergebnis Welche Vermutungen konntet ihr bestätigen? Welche Vermutungen mussten verworfen werden? Formuliert bestätigte Vermutungen als allgemeine Regel. Document1 QUA-LiS.NRW Variante B KPG Jgst. 9 Satz des Thales Erkundung Vorbereitung Zeichnet auf den Hof mit Kreide eine Strecke ̅̅̅̅ 𝐴𝐵 der Länge 5 m mit dem Mittelpunkt M. Schlagt mithilfe eines Bindfadens von 2,50 m Länge einen Halbkreisbogen um den Mittelpunkt M, der durch die Punkte A und B verläuft. Markiert auf dem Halbkreisbogen einen beliebigen Punkt 𝐶. Die Thales-Figur Stellt drei Personen auf: Je eine an die Punkte 𝐴, 𝐵 und 𝐶. Schätzt mit ausgestreckten Armen die Größe der Winkel des Dreiecks. Wie verändern sich die Winkel, wenn die Person 𝐶 auf dem Halbkreisbogen wandert? Ergebnis Was fällt euch auf? Beschreibt eure Beobachtungen. Formuliert anschließend begründete Vermutungen. Document1 QUA-LiS.NRW GA 1/2 Variante B KPG Jgst. 9 Satz des Thales Erkundung PA 2/2 Konstruktion Überprüft eure Vermutung vom Schulhof mit Hilfe eines DGS-Programms. Folgende Tipps können euch helfen: Öffnet ein Blatt in Eurem DGSProgramm und speichert es unter einem geeigneten Namen. Zeichnet eine beliebige ̅̅̅̅ und tragt den Strecke 𝐴𝐵 Mittelpunkt M ein. Zeichnet einen Halbkreis mit Mittelpunkt M und Radius ̅̅̅̅̅. 𝐴𝑀 Legt einen Punkt C fest: er soll auf dem Halbkreis liegen, dort aber beweglich sein. Zeichnet die Strecken ̅̅̅̅ 𝐴𝐶 und ̅̅̅̅ 𝐵𝐶 . Messt die drei entstandenen Winkel des Dreiecks ABC und notiert die Werte in einer geeigneten Tabelle. Bewegt C auf dem Halbkreis und messt jedes Mal die neu entstandenen Innenwinkel des Dreiecks. α β γ Ergebnis Welche Vermutungen konntet ihr bestätigen? Welche Vermutungen mussten verworfen werden? Formuliert bestätigte Vermutungen als allgemeine Regel. Document1 QUA-LiS.NRW Variante C KPG Jgst. 9 Satz des Thales Vorbereitung Zeichnet auf den Hof mit Kreide eine Strecke ̅̅̅̅ 𝐴𝐵 der Länge 5 m mit dem Mittelpunkt M. Schlagt mithilfe eines Bindfadens von 2,50 m Länge einen Halbkreisbogen um den Mittelpunkt M, der durch die Punkte A und B verläuft. Markiert auf dem Halbkreisbogen einen beliebigen Punkt 𝐶. Die Thales-Figur Stellt drei Personen auf: Je eine an die Punkte 𝐴, 𝐵 und 𝐶. Schätzt mit ausgestreckten Armen die Größe der Winkel des Dreiecks. Wie verändern sich die Winkel, wenn die Person 𝐶 auf dem Halbkreisbogen wandert? Ergebnis Was fällt euch auf? Beschreibt eure Beobachtungen. Formuliert anschließend begründete Vermutungen. Document1 QUA-LiS.NRW Erkundung GA 1/2 Variante C KPG Jgst. 9 Satz des Thales Erkundung PA 2/2 Konstruktion Überprüft eure Vermutung vom Schulhof mit Hilfe eines DGS-Programms. Folgende Tipps können euch helfen: Öffnet ein Blatt in Eurem DGSProgramm und speichert es unter einem geeigneten Namen. Zeichnet eine beliebige ̅̅̅̅ und tragt den Strecke 𝐴𝐵 Mittelpunkt M ein. Zeichnet einen Halbkreis mit Mittelpunkt M und Radius ̅̅̅̅̅. 𝐴𝑀 Legt einen Punkt C fest: er soll auf dem Halbkreis liegen, dort aber beweglich sein. Zeichnet die Strecken ̅̅̅̅ 𝐴𝐶 und ̅̅̅̅ . 𝐵𝐶 Messt die drei entstandenen Winkel des Dreiecks ABC und notiert die Werte in einer geeigneten Tabelle. Bewegt C auf dem Halbkreis und messt jedes Mal die neu entstandenen Innenwinkel des Dreiecks. α β γ Ergebnis Welche Vermutungen konntet ihr bestätigen? Welche Vermutungen mussten verworfen werden? Formuliert bestätigte Vermutungen als allgemeine Regel. Document1 QUA-LiS.NRW