Document

Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
1
4 ENTSCHEIDUNGEN BEI MEHREREN ZIELEN
4.1 Grundprobleme
4.2 Entscheidungskriterien für ordinal skalierte Zielgrößen
4.3 Nutzenbewertung bei mehreren Zielen
4.3.1 Visualisierung der Nutzenwerte
4.3.2 Zielgewichtung
4.3.3 Goal-Programming-Ansatz
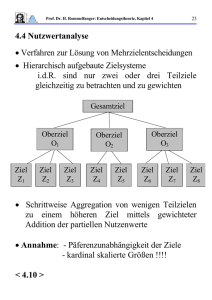
4.4 Nutzwertanalyse
4.5 Analytic Hierarchy Process (AHP)
4.6 Multi-Attribtive Nutzentheorie
4.7 Nutzwertanalyse mit Fuzzy-Nutzen
4.8 Fuzzy-AHP
4.9 Fuzzy-Logik basierte Mehrzielentscheidung
4.1 Grundprobleme bei mehrfacher Zielsetzung
In der betrieblichen Praxis sind für die Beurteilung und Auswahl
komplexer Projekte meist viele unterschiedliche Zielgrößen wichtig.
→ Entscheidungsmodelle mit mehreren Zielsetzungen
beschreiben daher die Realität in der Regel besser als
Entscheidungsmodelle mit nur 1 Zielgröße.
§ multikriterielle Entscheidungsmodelle (Alternativen
bekannt)
§ Vektoroptimierungsmodelle (Alternativen sind nicht
bekannt, sie werden durch Restriktionen eingeschränkt)
2
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
Probleme:
• Das Problem mehrfacher Zielsetzung liegt im Wesentlichen
darin, dass nur der R1 wohlgeordnet ist.
• Im R2 ist es oft noch möglich eine Lösung des 2-Ziel-Problems
zu erreichen, wenn es gelingt genügend viele Isoquanten, d. h.
Kurven mit äquivalenten Zielpaaren, anzugeben.
Z2
Z1
• Berücksichtigung qualitativer Zielgrößen (z.B. Servicegrad,
Mitarbeitermotivation, Image)
Beschreibung durch quantitative (= meßbare) Submerkmale
• Die Entscheidung bei mehreren Zielsetzungen ist unproblematisch, wenn eine Handlungsalternative bei allen Zielgrößen das jeweils höchste Ergebnis besitzt. (Ideale Lösung)
•
Die Entscheidung bei mehrfacher Zielsetzung ist problematisch, wenn Zielvorstellungen zumindest teilweise
miteinander im Konflikt stehen.
•
In ökonomischen Anwendungen ist die Anzahl der Ziele
sehr groß. Strukturierung als hierarchische Zielsysteme
3
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
Unabhängigkeit
Beziehung
zur Umwelt
Umweltschutz
Lieferanten unabhängigkeit
Kundenunabhängigkeit
Umweltfreundliche Produkte
Umweltfreundliche Produktion
Innovationsrate
Absatz
Marktwachstum
Marktanteil
Unternehmens
-leistung
Lagerumschlag
Produktion
Pro-Kopf-Leist.
Materialaufwandsquote
Selbstfinanzierungskraft
Dynamischer
Verschuldungsg.
Cash-Flow-Rate
Ertragslage
Umsatzrentabilität
Rentabilität
Gesamtkapitalrentabilität
Zielquote
Liquiditätslage
Liquidität II
Liquidität I
Gesamtanlagendeckungsgrad
Bilanzstruktur
Eigenkapitalqualität
Eigenkapitalquote
Hierarchisches System zur Bewertung der
Kreditwürdigkeit im Firmenkundengeschäft
4
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
Beispiel: Autokauf
6 Alternativen A1 – A6, 5 relevante Zielgrößen
Design
Motorleistung
Ausstattung
Werkstatt
A1 50.000 €
9
120 kW
6
3
A2 25.000 €
6
55 kW
4
8
A3 30.000 €
5
80 kW
8
5
A4 30.000 €
3
100 kW
8
7
A5 55.000 €
8
115 kW
6
2
A6 24.000 €
9
130 kW
9
8
Preis
Zielwerte beim Autokauf
- Bewertung von Design, Ausstattung, Werkstatt durch eine
Zehnpunkteskala, 10 = beste, 1 = schlechteste Bewertung
- Zielvorstellung des Autokäufers:
Preis möglichst gering, Motorleistung, Design, Ausstattung,
Werkstatt möglichst hoch
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
5
Prinzipiell: Entscheidungsfindung in 2 Schritten:
Schritt 1: Anwendung des Dominanzprinzips
Dominante ↔ dominierte Alternative
Effiziente ↔ ineffiziente Alternativen
à Elimination aller ineffizienten Alternativen
(zulässiger Lösungsraum
= Menge aller effizienten Aktionen)
- Für je 2 effiziente Aktionen existiert mindestens 1 Paar
von konfliktären Zielen.
- Auswahl zwischen Mehrerfüllung einiger Zielgrößen
und geringerer Erfüllung anderer Ziele
Schritt 2: Auswahlentscheidung zwischen den
effizienten, in Bezug auf die verfolgten
Zielsetzungen konkurrierenden Alternativen
à Wie schafft man es, daß die Alternativen vergleichbar
werden?
à Bestimmung einer Verknüpfungsregel (Funktionsgesetz)
durch die die verschiedenen Bewertungen einer Alternative
zu einem Gesamtpräferenzwert zusammengefasst werden
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
6
4.2 Entscheidungskriterien für ordinal skalierte
Zielgrößen
4.2.1 Transformationsprinzip
Beim LAUXschen Transformationsprinzip I werden
schrittweise nur zwei Zielgrößen miteinander verglichen.
< 4.2 > Zielgrößenmatrix { zk (ai ) }
Z1 Z2 Z3 Z4
a1 3 7 1 5
a2 10 4 15 6
Für jedes der 4 Ziele möchte der ET einen möglichst
hohen Zielwert erreichen.
1. Schritt:
z( a 2 ) = (10, 4, 15, 6) ∼ z2(a2) = (3, z 22 , 15, 6).
2. Schritt:
z2( a 2 ) = (3, z22, 15 , 6) ∼ z3(a2) = (3, 7, z 23, 6).
3. Schritt:
z3(a2) = (3, 7, z 23, 6) ∼ z4( a 2 ) = (3 , 7, 11 , z 24 )
Vergleich von z(a1) und z4(a2), die letzte Komponente
entscheidet.
Z1 Z2 Z3 Z4
a1 3 7 1 5
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
a2
3
7
7
1 z24
4.2.2 Zielunterdrückung
• Reduktion auf eine Ein-Ziel-Optimierung, Bestimmung
des wichtigsten Ziels
• Entscheidung nur unter Berücksichtigung dieses Zieles
mit höchster Priorität (= alleiniger Bewertungsmaßstab)
• Anwendung der "reinen" Zielunterdrückung akzeptiert
Vorliegen einer Indifferenzsituation
Beispiel: Autokauf
• Wichtigstes Ziel sei die Motorleistung:
• Wichtigstes Ziel sei die Ausstattung:
Kritik: Ist zwar sehr einfach, vernachlässigt aber vollkommen die anderen Ziele.
Situation vorstellbar, dass die ausgewählte
Alternative A* bei dem wichtigsten Ziel nur
wenig besser ist als eine andere Alternative A1.
Die Alternative A1 aber deutlich besser ist in
Bezug auf alle anderen Ziele.
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
8
4.2.3 Lexikographische Ordnung
• Bestimmung einer Rangordnung der Zielgrößen
• Die Anwendung der lexikographischen Ordnung bietet
bei Indifferenz die Möglichkeit im nächsten Schritt nach
der zweit-, dritt- usw. wichtigsten Zielgröße zu
entscheiden bis eine eindeutige Entscheidung gegeben
ist.
• Die Lexikographische Ordnung unterstellt keine
Substitution der verschiedenen Zielgrößen, sondern setzt
nur eine ordinale Präferenzordnung bezüglich der
verfolgten Zielkriterien voraus.
Beispiel: Autokauf
• Präferenzordnung:
Ausstattung f Preis f Motorleistung f Werkstatt f Design
Rangfolge der Alternativen:
• Präferenzordnung:
Preis f Design f Motorleistung f Werkstatt f Ausstattung
Rangfolge der Alternativen:
Vorteil: - Ordinale Präferenzordnung reichen aus
- Berücksichtigt alle Ziele
9
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
- Kann geeignet sein, wenn für alle Ziele
Mindestanforderungen bestehen
Kritik: Verzicht auf die Erfassung von Präferenzunterschieden bei den einzelnen Zielen.
Daher ist es möglich, dass ein kleiner Unterschied
bei bei einem erstrangigen Ziel die
Präferenzordnung festlegt, während erheblich
bessere Ausprägungen bei nachrangigen Zielen
nicht berücksichtigt werden.
4.2.4 Satisfizierung und Anspruchsniveauanpassung
• Optimierung versus Satisfizierung
• Setzen von Anspruchsniveaus für einige oder alle Ziele
(Formulierung v. Kick Out-Bedingungen oder K.O.Kriterien)
Beispiel Autokauf - Anspruchsniveaus :
Preis
≤ 40.000 €
Design Motorleistung Ausstattung Werkstatt
≥5
≥ 50 kW
≥4
≥5
→
• Informationen müssen vorliegen, um Anspruchniveaus
und Anspruchsniveauanpassung geeignet zu bestimmen
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
10
Bei Existenz von mehreren Alternativen, die den
Anspruchsniveaus genügen:
• Auswahl z.B. anhand einer lexikographischen Ordnung
der Ziele
Problem: Entscheidung nach subjektiver
Rangordnung der Zielkriterien
• Beibehaltung des Satisfizierungskonzepts durch
Anpassung der Anspruchsniveaus
4.3 Nutzenbewertung bei mehreren Zielen
• Bei Vorliegen mehrerer Ziele sind die Dimensionen der
Zielgrößen oft sehr unterschiedlich
• Verrechnungsproblematik (Anwendung von Entscheidungsregeln, die kardinal skalierte Daten verlangen.
problematisch!! )
• theoretisch elegante Lösung:
Abbildung der Ergebnisvektoren in die Menge der
reellen Zahlen mittels einer Gesamtnutzenfunktion
u: {(z1(a i ), z 2 (a i ),K , z K (a i ))} → R .
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
11
Eine abgeschwächte Variante besteht darin, zunächst die
Einzelergebnisse in Einzelnutzenwerte abzubilden. Dazu
sind Teilnutzenfunktionen zu bilden:
uk: {z k (a i )} → R , k = 1, 2, ..., m,
ZIEL: Normierte, d.h. vergleichbare Bewertungen
Zumeist Beschränkung der Wertemenge auf [0, 1]
VORAUSSETZUNG:
• Präferenzunabhängige Ziele
Falls die Präferenz zwischen Ergebnissen bezüglich des
einen Ziels davon abhängig ist, welches die Ergebnisse
der restlichen Ziele sind, ist die Bildung partieller
Nutzenfunktion sinnlos.
Beispiel für präferenzabhängige Ziele:
- Entscheidung über ein Abendessen
- Zielsetzungen „Getränk“ und „Hauptgang“
- jeweilige Ergebnismengen:
{Rotwein, Weißwein}, {Fisch, Steak}
- In der Regel ist die mehrheitliche Meinung, dass
Weißwein besser zu Fisch und Rotwein besser zu
Steak paßt.
→ D.H. es gelten die folgenden Präferenzaussagen:
(Rotwein, Steak) f (Weißwein, Steak) und
12
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
(Rotwein, Fisch) p (Weißwein, Fisch).
Isolierte Bewertung der Ergebnisse "Rotwein" bzw.
"Weißwein" nicht möglich, sondern kontextabhängig
• Nutzenfunktion muß den Zielbeziehungen Rechnung
tragen!!
- Zielindifferenz, Zielneutralität
(Design - Werkstatt)
- Zielkomplementarität, Zielharmonie
(Sitzkomfort - Ausstattung)
symmetrische Komplementarität
asymmetrische Komplementarität
- Zielkonkurrrenz, Zielkonflikt
(Preis - Motorleistung)
Bsp.: Autokauf
• Design, Ausstattung, Werkstatt: uki = uk(ai) = zk(ai)
.000 , Motorleistung: u(z) = z − 40
• Preis: u(z) = 10 − z −515
.000
10
Preis Design
A1
A2
A3
3
8
7
9
6
5
Motorleistung
8
1,5
4
AusWerkstatt
stattung
6
4
8
3
8
5
13
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
A4
7
A5 2
A6 8,2
3
8
9
6
7,5
9
8
6
9
7
2
8
Partielle Nutzenbewertungen beim Autokauf
4.3.1. Visualisierung von Mehr-Ziel-Problemen
Möglichkeiten der graphischen Darstellung der Nutzenverteilungen der Alternativen, um intuitive Auswahl der
optimalen Alternativen zu unterstützen:
• Zielstern
Beim Zielstern ist eine Alternative um so besser, je
näher der entsprechende Netzfaden am Sternmittelpunkt liegt.
14
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
Preis
Werkstatt
Design
Ausstattung
Motorleistung
Zielstern beim Autokauf
• Profilanalyse
Bei der Profilanalyse ist eine Alternative um so besser,
je weiter ihre Profillinie nach rechts verschoben ist.
Profilanalyse beim Autokauf
15
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
0
Preis
Design
Motorleistung
Ausstattung
Werkstatt
10
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
16
Andere Formen der Visualisierung sind Zielgesicht oder
Zielhaus.
Beim Zielgesicht wird ausgenutzt, dass einzelne Teile des
Gesichtes durch ihre Form zu einem zufriedenen oder
unzufriedenen Gesamteindruck beitragen.
Bekannteste Formen dürften dabei die Krümmungen des
Mundes sein, wobei gilt:
J voll zufrieden K gerade so zufrieden L unzufrieden
Andere ausdrucksstarke Partien sind die Augen (z. B. für
das rechte Auge)
voll zufrieden,
gerade so zufrieden,
unzufrieden,
die Wangen, die Stirn, die Ohren u. dgl..
Da aber nur wenige, zumeist drei, Ausprägungen zur Verfügung
stehen, müssen dafür die Nutzenwerte in Klassen gruppiert
werden, was zumeist durch Intervalleinteilung erfolgt, z. B. [7,5
; 10] voll zufrieden, ]3,5 ; 7,5[ gerade so zufrieden,
[1 ; 3,5] unzufrieden.
Hier ergibt sich das Problem, dass Elemente innerhalb einer
Klasse recht verschieden sein können, während Elemente in der
Nähe der Klassengrenzen unterschiedlichen Gruppen zugeordnet
werden, obwohl sie sich nur geringfügig unterscheiden.
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
17
Beim Zielhaus werden Fenster, Türen, Schornstein, Dach usw.
dann korrekt (gerade) gezeichnet, wenn das zugeordnete Ziel voll
zufrieden erfüllt ist. Je schiefer oder krummer das Bild, um so
unzufriedener ist der Entscheidungsträger mit dem
entsprechenden Zielwert.
18
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
4.3.2 Zielgewichtung
• Formal:
Pro Aktion werden die partiellen Nutzenwerte uk(ai)
der Zielkriterien zk mit nichtnegativen Gewichten gk (k
= 1, 2, …, K) multipliziert und die gewichteten
Nutzenwerte aufaddiert:
K
u(ai) = g1 ⋅ u1( a i )+K+g K ⋅ u K ( a i ) = ∑ g k ⋅ u k (a i ) .
k =1
Die Aktion a* mit dem höchsten Gesamtnutzenwert
u(a*) ist optimal.
Voraussetzungen:
• gegenseitige Substitution der Zielgrößen und
• kardinale Nutzenmessung
• der Entscheider muss in der Lage sein, individuelle
Zielgewichtungsfaktoren für jedes Ziel zu bestimmen,
d.h. Faktoren, die das Verhältnis der Nutzenwerte der einzelnen Ergebnisse zum Gesamtnutzen der Aktion fixieren
• In der Regel werden die Gewichtungsfaktoren so
normiert, dass ihre Summe gleich 1 ist.
• Ein anerkannter Weg zur Bestimmung von Zielgewichten ist die Bestimmung von Austauschrelationen
zwischen den Ausprägungen der Zielgrößen.
19
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
Austauschrelationen geben an, wie viel Mehrerfüllung des einen Ziels äquivalent ist zu einer Mindererfüllung eines anderen Ziel.
• Bezeichnen wir die Gewichte zu den Zielen k und r
mit g k und g r , so ist die Austausch- oder
gr
Substitutionsrate αkr =
definiert als der Faktor,
gk
um den der Nutzenwert bezüglich des Ziels k erhöht
werden muss, wenn der Nutzenwert des Ziels r um
den absoluten Wert ∆ reduziert wird,
d. h. αkr ⋅ ∆ ⋅ g k = ∆ ⋅ g r .
Beispiel: Autokauf
AusWerk- GesamtPreis Design Motorleistung stattung statt
nutzen
g k 0,3
A1
A2
A3
A4
U(a4) =
3
8
7
7
0,2
0,1
0,2
0,2
9
6
5
3
8
1,5
4
6
6
4
8
8
3
8
5
7
5,3
6,15
6,1
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
20
4.3.3 Goal Programming
• Annahme: Entscheider erhält numerische Vorgaben ẑ k
(Punktziele), die er möglichst gut erreichen soll.
• Zielvorgaben im Idealfall so abgestimmt, daß sie sich
alle gleichzeitig realisieren lassen, ansonsten je nach
Alternative positive und negative Abweichungen von
den Zielvorgaben möglich.
• optimale Alternative:
Diejenige Alternative, deren Ergebnis den geringsten
"Gesamtabstand" zu den Zielvorgaben aufweist
d.h. Minimierung der Summe der absoluten
Abweichungen von den Zielvorgaben!
• Der Goal-Programming-Ansatz lässt sich formal
schreiben als
K
Min ∑ gk ⋅ (û k −u k (a))
a∈A k =1
K
mit ∑ g k ⋅ (û k −u k (a )) als Regretfunktion
k =1
-
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
-
-
21
Starrer Ansatz des Goal Programming:
Zielvorgaben werden durch die individuellen Maxima
der Zielgrößen der relevanten Aktionen gegeben.
û k = Max u k (a ) ,
a∈Ae
wobei Ae die Menge der effizienten Lösungen aus A
ist.
Flexibler Ansatz des Goal Programming:
Zielvorgaben werden festgelegt unabhängig von den
Ausprägungen der relevanten Aktionen.
û k = u k (ẑ k ) Nutzenwert der Zielvorgabe ẑ k ,
• Ein Problem des Goal-Programming-Ansatzes ist die
Wahl der Gewichte. Daher wird häufig eine Gleichgewichtung der Ziele vorgenommen.
22
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
Beispiel: Starrer Ansatz
Preis Design
A1
A2
A3
A4
Â
0,3
3
8
7
7
8
0,2
9
6
5
3
9
Motorleistung
Ausstattung
Werkstatt
0,1
8
1,5
4
6
8
0,2
6
4
8
8
8
0,2
3
8
5
7
8
Regretwert
A1
A2
A3
A4
Flexibler Ansatz – Zielvorgaben von außen
Preis Design
A1
A2
Motorleistung
Ausstattung
Werkstatt
0,3
0,2
0,1
0,2
0,2
3
8
9
6
8
1,5
6
4
3
8
Regretwert
3,4
2,55
23
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
A3
A4
7
7
5
3
4
6
8
8
5
7
Â
9
9
8
9
8
2,6
2,4
Alternative Nutzenorientierung nach Körth 1969
Gesamtzufriedenheit mit ai wird definiert als
u k (a i )
u(a i ) = Min {
},
k Max u k (a )
a∈Ae
d. h.
üder ungünstigste relative Zielerreichungsgrad gibt den
Ausschlag,
ü eine Kompensation mit höheren Zielerreichungsgraden findet nicht statt.
ü Die Alternative, die dann den höchsten Wert aufweist,
wird als optimal bestimmt.
Preis Design
A1
A2
A3
A4
MotorAusWerk- Regretleistung stattung statt
wert
0,3
0,2
0,1
0,2
0,2
3
8
7
7
9
6
5
3
8
1,5
4
6
6
4
8
8
3
8
5
7
3,4
2,55
2,6
2,4
24
Prof. Dr. H. Rommelfange: Entscheidungstheorie, Kapitel 4
1
A1 0,375
1
0,67
A2
A3 0,875 0,56
A4 0,8757 0,33
1
0,1875
0,5
0,75
0,75
0,5
1
1
0,375 0,375
1
0,1875
0,625 0,5
0,875 0,33