4.4 Nutzwertanalyse • Verfahren zur Lösung von

23
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
4.4 Nutzwertanalyse
• Verfahren zur Lösung von Mehrzielentscheidungen
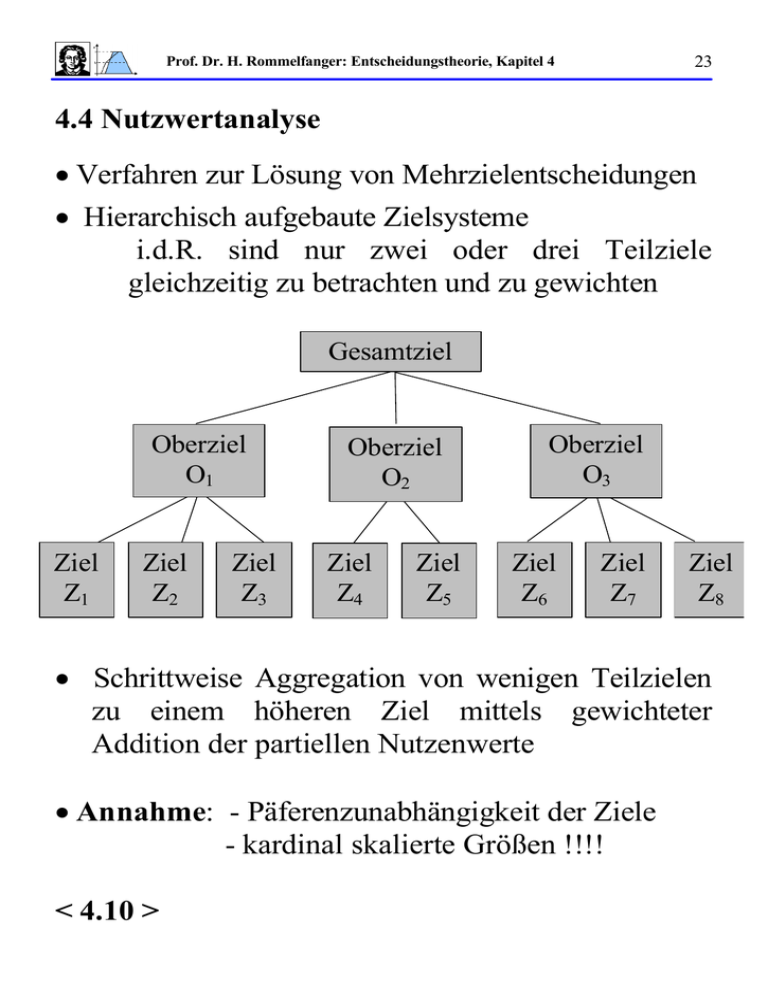
• Hierarchisch aufgebaute Zielsysteme
å i.d.R. sind nur zwei oder drei Teilziele
gleichzeitig zu betrachten und zu gewichten
Gesamtziel
Oberziel
O1
Ziel
Z1
Ziel
Z2
Ziel
Z3
Oberziel
O2
Ziel
Z4
Ziel
Z5
Oberziel
O3
Ziel
Z6
Ziel
Z7
Ziel
Z8
• Schrittweise Aggregation von wenigen Teilzielen
zu einem höheren Ziel mittels gewichteter
Addition der partiellen Nutzenwerte
• Annahme: - Päferenzunabhängigkeit der Ziele
- kardinal skalierte Größen !!!!
< 4.10 >
24
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
Gesamtbewertung
des Autokaufs
0,3
Bewertung des
Kaufpreises
0,4
Bewertung des
Design
0,5
Bewertung des
Autos
0,2
Bewertung der
Motorenleistung
0,2
Bewertung der
Werkstatt
0,4
Bewertung der
Ausstattung
Entscheidungsregel: Auswahl der Alternative
mit höchstem (Gesamt-)Nutzenwert !
• Zentrale Elemente der Nutzwertanalyse:
∗ (partielle) Nutzenwerte
∗ Gewichte der Zielkriterien
Ermittlung der Nutzenwerte
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
25
(nach Zangemeister 1972)
å Projektion der Zielerreichungsgrade in das Intervall
[0, 10] mit Hilfe von darüber gelegten, verbal
erläuterten Intervallklassen
"sehr schlecht":
"schlecht":
"durchschnittlich":
"gut":
"sehr gut":
[0 , 2[
[2 , 4[
[4 , 6]
]6 , 8]
]8 , 10]
å wahrheitsgetreue und eindeutige Nutzenwertzuordnung??!!
Realistischer dürften Fuzzy-Nutzenwerte über [0 , 10] !!
26
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
Ermittlung der Zielgewichte
• Bestimmung der Gewichte über Ermittlung der
paarweisen Austauschraten zwischen den Zielen
a kr ⋅ ∆ ⋅ g k = ∆ ⋅ g r
(Paarvergleichsmatrizen)
g
a kr = r > 0 , k, r ∈ {1,...,K}
gk
• Austauschrate
Preis
Auto
Werkstatt
Preis
1
1
2
3
2
Auto
2
1
3
Werkstatt
2
3
1
3
1
å Speziell gilt:
g
a kk = k = 1
gk
gk
1
a rk =
=
g r a kr
für k = r
reziproke Paarvergleichsmatrix
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
27
• Konsistenzbedingung für Paarvergleichsmatrix !!
å widerspruchsfreie Präferenzen
g g
g
a kr ⋅ a rs ( = r ⋅ s = s ) = a ks
g k gr g k
v in einer konsistenten Paarvergleichsmatrix sind
alle Spaltenvektoren Vielfache voneinander
und jede Spalte stellt somit einen äquivalenten
Gewichtevektor dar!
v normierter Gewichtevektor:
Austauschraten sind dann eindeutig bestimmt,
wenn die Summe der Gewichte auf 1 normiert
wird.
Preis
Auto W.statt
Preis
1
1
2
3
2
Auto
2
1
3
W.statt
2
3
1
3
1
3
 11   0,2727 
 6  ≈  0,54554 

 11  

 2   0,1818 
 11 
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
28
4.5 Analytic Hierarchy Process (AHP)
(THOMAS L. SAATY 1980)
• Basis: konsistente, reziproke Paarvergleichsmatrix
å Bewertung der Paarvergleiche mit Hilfe der 9Punkteskala von SAATY
1
3
5
7
9
2,4,
6,8
Beide verglichenen Elemente
haben die gleiche Bedeutung für
das nächst-höhere Element (Ziel).
Erfahrung und Einschätzung
etwas größere
sprechen für eine etwas größere
Bedeutung
Bedeutung
Erfahrung und Einschätzung
erheblich größere
sprechen für eine erheblich
Bedeutung
größere Bedeutung
sehr viel größere Die sehr viel größere Bedeutung
eines Elements hat sich in der
Bedeutung
Vergangenheit klar gezeigt
Es handelt sich um den größtmögabsolut
lichen Bedeutungsunterschied
dominierend
zwischen Elementen
Zwischen zwei benachbarten
Zwischenwerte Urteilen muß eine Übereinkunft
getroffen werden, ein Kompromiß
gleiche
Bedeutung
→ Nur ordinalskalierte Paarvergleiche
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
29
→ Unklare Definition der Präferenzen
• Alternative Berechnung des normierten Gewichtevektors:
Im Fall einer konsistenten Paarvergleichsmatrix A
entspricht der Gewichtevektor g dem Eigenvektor
x zum größten Eigenwert λ von A
A ⋅x = λ ⋅x
Weiterhin gilt, dass der größte Eigenwert einer
konsistenten Paarvergleichsmatrix A stets gleich der
Ordnung von A ist und alle übrigen Eigenwerte
gleich 0 sind.
( A − λE) ⋅ x = 0
Determinantentheorie!!!
< 4.12 > bekannte Paarvergleichsmatrix aus < 4.8 >
1− λ
1
2
3
2
2
1− λ
3
2
3
1
3
1− λ
= λ2 (3 − λ ) = 0
⇒ Eigenwerte λ1 = 3 und λ 2,3 = 0
⇒ Eigenvektor zu λ1 = 3:
( 3 , 3 , 1) ⋅ t , t ∈ R ,
2
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
30
⇒ Norm. Gewichtevektor (0,2727 ,0,54554 ,0,1818)
• Häufiges Problem bei realen Anwendungen:
Entscheider formulieren inkonsistente Paarvergleichsmatrizen. Diese widersprüchlichen Präferenzen sind das Ergebnis einer beschränkten
Informationsverarbeitungskapazität
Vorschlag von THOMAS SAATY:
∗ Bei kleineren Verstößen gegen die Konsistenzbedingung sollte weiterhin als Gewichtevektor der
Eigenvektor zum größten Eigenwert von A
verwendet werden. Nach SAATY, solange
KI ( A )
der Konsistenzwert KW(A) =
≤ 0,1 ist.
RI
λ max − n
- Konsistenzindex KI =
n −1
- Random Index (RI) = durchschnittlicher Konsistenzindex, der sich ergibt, wenn reziproke
Zufallsmatrizen auf Grundlage der SAATYschen
Skala erzeugt werden
n
RI(n)
n
1
0
9
2
0
10
3
4
5
6
7
8
0,58 0,90 1,12 1,24 1,32 1,41
11
12
13
14
15
31
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
RI(n) 1,45 1,48 1,49 1,51 1,56 1,57 1,5
< 4.13 >
Design
Design
Motorleistung
Ausstattung
Motorleist.
1
7
Ausstattung
1
2
7
1
3
2
1
3
1
1
⇒ inkonsistente Paarvergleichsmatrix B, da
• z. B. b 21 ⋅ b13 = 7 ⋅ 1 ≠ b 23 = 3
2
• maximaler Eigenwert nicht gleich 3,
sondern näherungsweise λ max = 3,0026437
• KW(B) =
3.0026437 − 3
3−1
= 0,002279 ≤ 0,1
0,58
⇒ ausreichend konsistent
• Eigenvektor zu λ max : (1; 6,6494; 2,1054)⋅t, t∈R
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
32
• Norm. Gewichtevektor: (0,1025; 0,6816; 0,2158).
• Gewichte für Design, Motorleistung und Ausstattung durch Multiplikation dieser Gewichte mit dem
Gewicht für die Bewertung der Attribute eines
Autos
Gesamtbewertung
des Autokaufs
Bewertung des
Kaufpreises
Bewertung des
Autos
Bewertung des
Design
Bewertung der
Motorenleistung
Preis
Design
Bewertung der
Werkstatt
Bewertung der
Ausstattung
Motor- AusWerk- Gesamtleistung stattung statt
nutzen
w 0,2727 0,0559 0,3717 0,1177 0,1818
3
9
8
6
3
5,5464
A1
8
6
1,5
4
8
4,9998
A2
7
5
4
8
5
5,5258
A3
7
3
6
8
7
A4
6,5210
33
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
• Ermittlung der Teilnutzenwerte
å analoge Vorgehensweise (Eigenvektor):
Zuweisung von Nutzenwerten zwischen 0 und 1
å Zielhierarchie erhält zusätzliche Ebene
Ziel Zk
Alternative
A1
Alternative
A2
Alternative
A3
å sinnvoll nur bei wenigen Alternativen
Alternative
A4
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
34
< 4.14 > relative Nutzenbewertung "Motorleistung":
A1 A2 A3 A4
A1 1
8
5
2
A2
A3
A4
1
8
1
5
1
2
1
1
3
3
1
5
3
1
5
1
3
1
• inkonsistente 4×4-Paarvergleichsmatrix, da z. B.
gilt c12 ⋅ c 23 = 8 ≠ c13 = 5.
3
• maximale Eigenwert λ max = 4,0516145 .
• Da KW(C) =
4,0516145 − 4
÷ 0,9 = 0,019116 ≤ 0,1,
4 −1
ist die Paarvergleichsmatrix noch ausreichend
konsistent
• normierter Eigenvektor
(0,5316; 0,0542; 0,1202; 0,2940)
als relativer Nutzenvektor
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4
35
Kritik:
• Zielgewichtung
kriterium???
als
geeignetes
Aggregations-
• Paarvergleiche sind ordinalskaliert;
Bestimmung der reziproken Werte/Berechnung der
Gewichteverteilung erfordert Verhältnis- bzw.
Kardinalskalenniveau
• Saatys 9-Punkte-Skala ist rational nicht
gerechtfertigt und angreifbar
→ andere Skalen können zu anderen Rangordnungen der Alternativen führen
→ Ergebnis: Rangordnungen differieren jeweils
unterschiedlich stark in Abhängigkeit der Anzahl
von Alternativen, Kriterien und Verteilungen.
• Definition der Präferenz in den Paarvergleichen
äußerst schwammig
• praktische Erfahrungen: Anwender verstehen
Austauschraten eher im dem Sinne, daß ein Ziel xmal wichtiger als ein anderes ist.