Elektromagnetischer Schwingkreis 1. Grundlagen CLUI U0 S - sfz-bw

. September 
100913Ph4-Schwingkreis.TEX
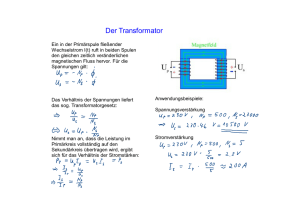
Elektromagnetischer Schwingkreis
Dorn-Bader S. 108 ff.
Bei freien mechanischen Schwingungen wandeln sich Elongationsenergie und Bewegungsenergie
periodisch ineinander um. Solche Energiependelungen gibt es auch bei elektrischen und magnetischen Feldern in Kondensatoren und Spulen.
1.
Grundlagen
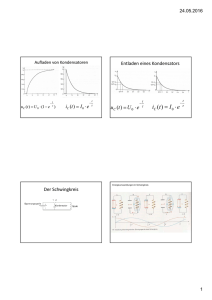
Entlädt man (vgl. Abb. ??) einen Kondensator über eine Spule, so verschwindet sein elektrisches Feld mit
seiner elektrischen Energie. Dafür fließt durch die Spule ein Strom, der ein Magnetfeld mit magnetischer Feldenergie aufbaut. Verschwindet das Magnetfeld seinerseits, so entsteht eine Induktionsspannung, welche
den Strom in seiner ursprünglichen Richtung weitertreibt und den Kondensator umgekehrt auflädt, und
damit wieder ein elektrisches Feld.
Versuch Dorn-Bader V1 und Abb. B2
C
L
A BB . 1 (Idealer) Elektrischer Schwingkreis
S
I
U
L
U0
C
A BB . 2 Elektrischen Schwingkreis
A BB . 3
Eine Spule mit etwa 1000 Windungen und ein Kondensator mit der Kapazität C = 1 µF werden zu
einem Kreis zusammengeschlossen. Mit einem Schalter kann man den Kondensator z. B. über eine
10 V Gleichspannungsquelle aufladen und dann über die Spule entladen.
Man beobachtet, wenn man den Strom- und Spannungsverlauf mit dem CASSY aufnimmt, dass
Strom und Spannung gedämpfte Schwingungen ausführen. Spannung und Strom sind dabei um π2
phasenverschoben.
Ein Stromkreis aus Kondensator und Spule heißt elektromagnetischer Schwingkreis. In einem
solchen Schwingkreis findet eine periodische Energieumwandlung zwischen elektrischer und
magnetischer Energie statt. Stromstärke und Spannung sind dabei um π2 phasenverschoben.

. September 
100913Ph4-Schwingkreis.TEX
Bei einem idealen Schwingkreis wird vom ohmschen Widerstand der Zuleitungen und Spule abgesehen. Der Schwingkreis schwingt ungedämpft.
Mechanische und elektromagnetische Schwingungen haben viel Ähnlichkeit miteinander.
Schülerarbeit:
Vergleiche die verschiedenen
Schwingungsphasen eines Federpendels
mit
denen
eines
Schwingkreises
(Dorn-Bader S. 109).
A BB . 4
2.
Differentialgleichung (DGl) des Schwingkreises
Für einen (ungedämpften) elektromagnetischen Schwingkreis sind nur Kondensator und Spule parallel geschaltet.
Q(t)
Es gilt stets: UC = US = −Uind . Mit UC (t) =
und
L
++++++++
C
1
UC
C
US
Uind = − L İ (t) folgt İ (t) =
Q(t). Da für die Strom-------LC
stärke I (t) = − Q̇(t) ist, gilt (vgl. Schwingungsgleichung
D
s̈ = − s)
m
A BB . 5 Spannung und Strom im elektrischen
1
Schwingkreis
Q̈(t) = −
·Q
LC
b sin(ωt + ϕ0 ) lösen.
Diese DGl lässt sich somit dem Ansatz Q = Q
I
Die Konstante ϕ0 errechnet sich wie bei den mechanischen Schwingungen aus den Anfangsbedingungen.
√
Für die Periodendauer gilt T = 2π LC (Thomsonsche Schwingungsgleichung)
Übungen Dorn-Bader S. 111 A1 und A2
3.
Energiesatz beim (ungedämpften) Schwingkreis
Im Schwingkreis wandeln sich elektrische und magnetische Feldenergie periodisch ineinander um.
In jedem Augenblick bleibt dabei die Summe dieser beiden Energien erhalten.

. September 
100913Ph4-Schwingkreis.TEX
b cos(ωt))
Für die Energie des elektrischen Feldes im Kondensator gilt (o.B.d.A. U (t) = U
1
1 b2
CU 2 (t) = CU
cos2 ωt
2
2
Für die Energie des magnetischen Feldes in der Spule gilt
Wel (t) =
1 2
1 2
LI (t) = L b
I sin2 ωt
2
2
r
C
b
b
Beim Lösen der DGl zeigte sich, dass I = U
ist. So folgt
L
Wmag (t) =
W=
4.
1 b2
1 b2 C
1 b2
1 b2
CU cos2 ωt + LU
sin2 ωt = CU
(cos2 ωt + sin2 ωt) = CU
2
2
L
2
2
Meißnersche Rückkopplungsschaltung
vgl. mechanische Rückkopplungsschaltung
Versuch Dorn-Bader S. 115 V3
Statt des NPN Transistors eignet sich
noch besser ein FET.
<
=
0
>
1
2
?
3
@
;4
5
6
/7
8
9
:.A
-B
+
,C
*#
D
$
%
)"E
(F
!&
G
'K
JH
L
M
IN
~
O
}P
|m
Q
u
w
v{zyxtR
sln
ko
p
q
rS
T
jU
g
h
V
ià
b
d
ce
W
f_
^]X
\Y
Z
[
10kΩ
A BB . 6
A BB . 7
Wird im richtigen Augenblick die dem Schwingkreis verlorengegangene Energie ersetzt, so erhält
man eine ungedämpfte elektromagnetische Schwingung. Der Transistor wird vom Schwingkreis
über eine Rückkopplungsspule gesteuert. Er verhält sich so, dass stets im richtigen Zeitpunkt dem
Schwingkreis eine Energiespritze verpasst wird. Die anfangs schwache elektromagnetische Schwingung schaukelt sich immer weiter auf, bis die während einer Periode entstehenden Dämpfungsverluste durch die von der Batterie gelieferten Energiezufuhren gerade ausgeglichen werden.
5.
Erzwungene Schwingungen
vgl. Dorn-Bader S.117 V2 - Experimente dazu im Praktikum
Übungen Dorn-Bader S. 124 A1, A2, A4
