-334bungen f-374r die Mathearbeit - quadratische Gleichungen

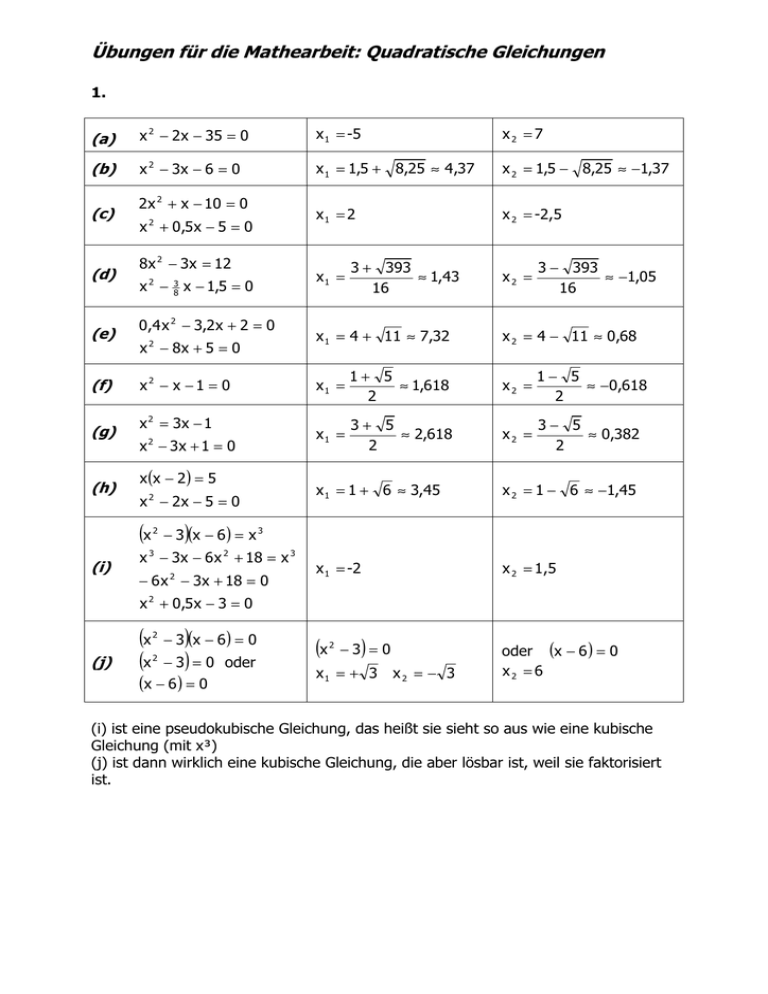
Übungen für die Mathearbeit: Quadratische Gleichungen
1.
(a)
x 2 − 2 x − 35 = 0
x 1 = -5
x2 = 7
(b)
x 2 − 3x − 6 = 0
x 1 = 1,5 + 8,25 ≈ 4 ,37
x 2 = 1,5 − 8,25 ≈ −1,37
x1 = 2
x 2 = -2,5
(c)
(d)
(e)
(f)
(g)
2 x 2 + x − 10 = 0
x 2 + 0,5 x − 5 = 0
8x 2 − 3x = 12
2
3
8
x − x − 1,5 = 0
0,4 x 2 − 3,2 x + 2 = 0
x 2 − 8x + 5 = 0
x2 − x − 1 = 0
x 2 = 3x − 1
2
x − 3x + 1 = 0
(h)
x (x − 2 ) = 5
x 2 − 2x − 5 = 0
(x
2
x1 =
3 + 393
≈ 1,43
16
x 1 = 4 + 11 ≈ 7,32
x2 =
3 − 393
≈ −1,05
16
x 2 = 4 − 11 ≈ 0,68
x1 =
1+ 5
≈ 1,618
2
x2 =
1− 5
≈ −0,618
2
x1 =
3+ 5
≈ 2,618
2
x2 =
3− 5
≈ 0,382
2
x 1 = 1 + 6 ≈ 3,45
x 2 = 1 − 6 ≈ −1,45
x 1 = -2
x 2 = 1,5
(x
oder (x − 6 ) = 0
x2 = 6
)
− 3 (x − 6 ) = x 3
3
(i)
x − 3x − 6 x 2 + 18 = x 3
− 6 x 2 − 3x + 18 = 0
x 2 + 0,5 x − 3 = 0
(j)
(x
(x
2
2
)
− 3) = 0
− 3 (x − 6 ) = 0
(x − 6 ) = 0
oder
2
)
−3 =0
x1 = + 3 x 2 = − 3
(i) ist eine pseudokubische Gleichung, das heißt sie sieht so aus wie eine kubische
Gleichung (mit x³)
(j) ist dann wirklich eine kubische Gleichung, die aber lösbar ist, weil sie faktorisiert
ist.
Übungen für die Mathearbeit: Quadratische Gleichungen
2.
(a)
reinquadratische Gleichung:
x 1 = +
20
x 2 − 20 = 0
(b)
5 
x

 x −  8 −  = 0
6 
9

(c)
34 − 3x − x 2 = 3(3 − x )
x 2 = − 20
faktorisiert:
5
x


 x −  = 0 oder  8 −  = 0
6
9


5
x1 =
oder x 1 = 72
6
34 − 3x − x 2 = 9 − 3x
25 = x 2
x1 = + 5
oder x 1 = − 5
3. Du hast hoffentlich an den Definitionsbereich gedacht ☺
(a)
x −1 =
(b)
2 x + 23
x +1
x ≠ −1
(x − 1 )(x + 1 ) = 2 x + 23
x 2 − 1 = 2 x + 23
x 2 − 2 x − 24 = 0
x 1 = − 4 oder x 1 = 6
42 − 30 x
= 3x + 6
7−x
42 − 30 x = (3x + 6 )(7 − x )
3x 2 − 45x = 0
3x (x − 15 )
x1 = 0
oder x 1 = 15
4. (individuelle Lösung)
5. Für welche Werte von a hat die Gleichung x 2 = −ax − 3 eine bzw. zwei
2
a
Lösungen? Die Diskriminante ist D =   − 3 . Die Gleichung D=0 liefert die
2
beiden Lösungen a1 = + 12
und a 2 = − 12
6. Finde zwei Zahlen, deren Summe gleich 7,5 und deren Produkt 14 ist.
Die eine Zahl ist x. Dann ist die andere Zahl 7,5 – x. Die Gleichung x (7,5 − x ) = 14
liefert die Lösungen 4 und 3,5. Das sind die beiden gesuchten Zahlen.
Übungen für die Mathearbeit: Quadratische Gleichungen
7. Ein Rechteck hat den Umfang 20cm und die Fläche 5cm².
Wie lang sind seine Seiten?
Für den Umfang gilt 2a+2b=20 (cm), also a+b=10 oder b=10-a
Für die Fläche ergibt sich die Gleichung a(10 − a) = 5 mit den Lösungen
a1 = 5 + 20 ≈ 9,5
und a 2 = 5 − 20 ≈ 0,5
8. Ein Blumenbeet von 3m Länge und 2m Breite ist ringsum mit konstanter Breite
von Rasen eingefasst, so dass die Einfassung und das Beet den gleichen
Flächeninhalt haben.
Wie breit ist die Einfassung?
Die Aufgabe kann unterschiedlich verstanden werden:
Für die gesamte Fläche gilt:
(3 + 2x )(2 + 2x ) = 2 ⋅ 6
mit den Lösungen -3 und 0,5.
Die negative Lösung hat hier keinen
Sinn, also ist die Einfassung 0,5m breit.
Für das Beet ohne die Einfassung gilt:
(3 − 2x )(2 − 2x ) = 6
2
mit den Lösungen 2,15 und 0,35 (etwa).
Die Lösung 2,15 geht hier wegen der
Maße des Beetes nicht, also ist die
Einfassung 35cm beit