Document
Werbung
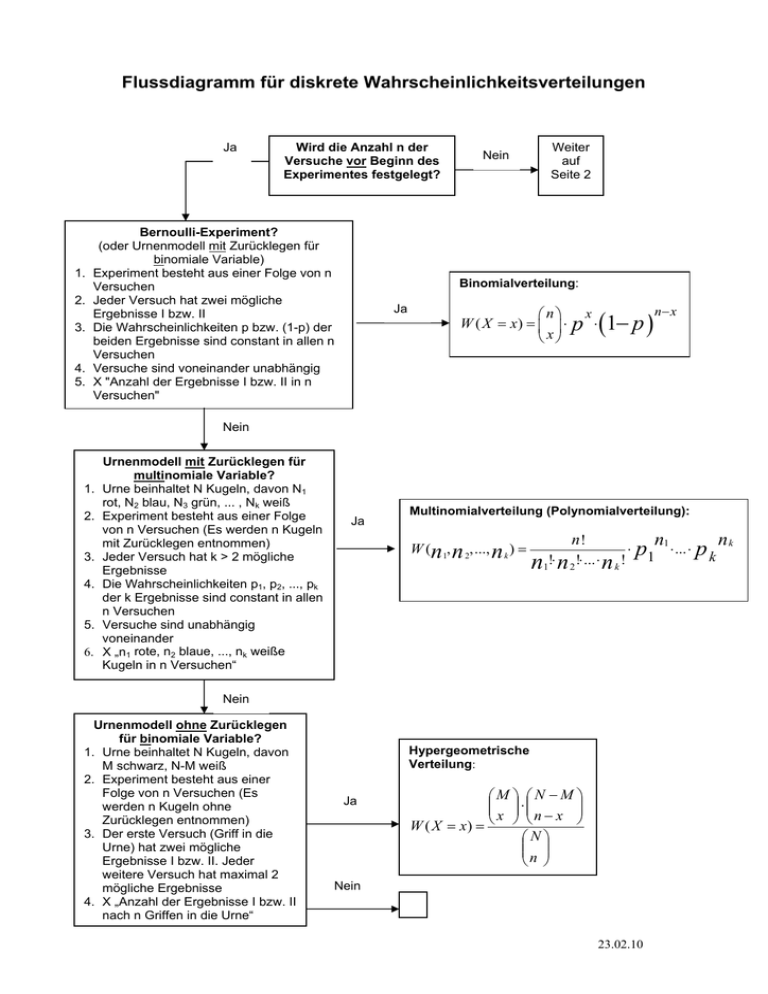
Flussdiagramm für diskrete Wahrscheinlichkeitsverteilungen Ja 1. 2. 3. 4. 5. Wird die Anzahl n der Versuche vor Beginn des Experimentes festgelegt? Bernoulli-Experiment? (oder Urnenmodell mit Zurücklegen für binomiale Variable) Experiment besteht aus einer Folge von n Versuchen Jeder Versuch hat zwei mögliche Ergebnisse I bzw. II Die Wahrscheinlichkeiten p bzw. (1-p) der beiden Ergebnisse sind constant in allen n Versuchen Versuche sind voneinander unabhängig X "Anzahl der Ergebnisse I bzw. II in n Versuchen" Nein Weiter auf Seite 2 Binomialverteilung: Ja ⎛n⎞ W ( X = x) = ⎜ ⎟ ⋅ ⎝ x⎠ p (1− p ) x ⋅ n− x Nein 1. 2. 3. 4. 5. 6. Urnenmodell mit Zurücklegen für multinomiale Variable? Urne beinhaltet N Kugeln, davon N1 rot, N2 blau, N3 grün, ... , Nk weiß Experiment besteht aus einer Folge von n Versuchen (Es werden n Kugeln mit Zurücklegen entnommen) Jeder Versuch hat k > 2 mögliche Ergebnisse Die Wahrscheinlichkeiten p1, p2, ..., pk der k Ergebnisse sind constant in allen n Versuchen Versuche sind unabhängig voneinander X „n1 rote, n2 blaue, ..., nk weiße Kugeln in n Versuchen“ Ja Multinomialverteilung (Polynomialverteilung): W (n1, n 2,..., n k ) = n! n1!⋅ n 2 !⋅ ... ⋅ n k ! ⋅ p1n1 ⋅ ... ⋅ p k n k Nein Urnenmodell ohne Zurücklegen für binomiale Variable? 1. Urne beinhaltet N Kugeln, davon M schwarz, N-M weiß 2. Experiment besteht aus einer Folge von n Versuchen (Es werden n Kugeln ohne Zurücklegen entnommen) 3. Der erste Versuch (Griff in die Urne) hat zwei mögliche Ergebnisse I bzw. II. Jeder weitere Versuch hat maximal 2 mögliche Ergebnisse 4. X „Anzahl der Ergebnisse I bzw. II nach n Griffen in die Urne“ Hypergeometrische Verteilung: Ja ⎛M ⎞ ⎛N − M ⎞ ⎜⎜ ⎟⎟ ⋅ ⎜⎜ ⎟ x ⎠ ⎝ n − x ⎟⎠ ⎝ W ( X = x) = ⎛N⎞ ⎜⎜ ⎟⎟ ⎝n ⎠ Nein 23.02.10 Fortsetzung von Seite 1 Urnenmodell mit Zurücklegen für binomiale Variable? 1. Urne beinhaltet N Kugeln, davon M schwarz und N-M weiß 2. Es wird mit Zurücklegen so oft in die Urne gegriffen, bis zum ersten Mal eine schwarze Kugel auftaucht. 3. Jeder Versuch (Griff in die Urne) hat zwei mögliche Ergebnisse I bzw. II 4. Die Wahrscheinlichkeiten p bzw. (1-p) der beiden Ergebnisse sind constant in allen Versuchen 5. Versuche sind unabhängig voneinander 6. X „Nummer des Griffes in die Urne, bei dem zum ersten Mal schwarze Kugel auftaucht“ Geometrische Verteilung: Ja W ( X = x) = Nein Obiges Experiment wird so oft durchgeführt bis zum r-ten Mal schwarze Kugel auftaucht? X „Nummer des Griffes in die Urne, bei dem zum r-ten Mal schwarze Kugel auftaucht“ (x≥r) Ja (1− p ) x−1 Negative Binomialverteilung: ⎛ x − 1⎞ r W ( X = x) = ⎜ ⎟⋅ p ⋅ ⎝ r −1⎠ Nein Poisson-Experiment? 1. Das Experiment besteht im Zählen eines bestimmten Ereignisses pro Zeit-, Längen-, Flächen- bzw. Volumeneinheit 2. Die Zahl der Ereignisse, die in einer Einheit (z. B. Stunde) gemessen werden, ist unabhängig von der Zahl der Ereignisse, die in irgendeiner anderen Einheit (Stunde) gemessen werden 3. Die Wahrscheinlichkeit, daß ein Ereignis in einer bestimmten Einheit (z. B. Stunde) eintritt, ist die selbe für alle Einheiten (Stunden), und sie ist proportional zur Länge der Einheit 4. Die durchschnittliche Zahl von Ereignissen pro Einheit (z. B. Stunde) ist μ 5. Die Wahrscheinlichkeit, daß mehr als ein Ereignis in einer Einheit (z. B. Zeit/Stunde) eintritt, geht gegen Null, wenn die Einheit immer kleiner wird. 6. X “Anzahl der Ereignisse pro Zeit-, Längen-, Flächen- bzw. Volumeneinheit“ Nein ⋅p Ja Poissonverteilung: −μ ⋅e μ W ( X = x) = x x! (1− p ) x −r











