Lösung

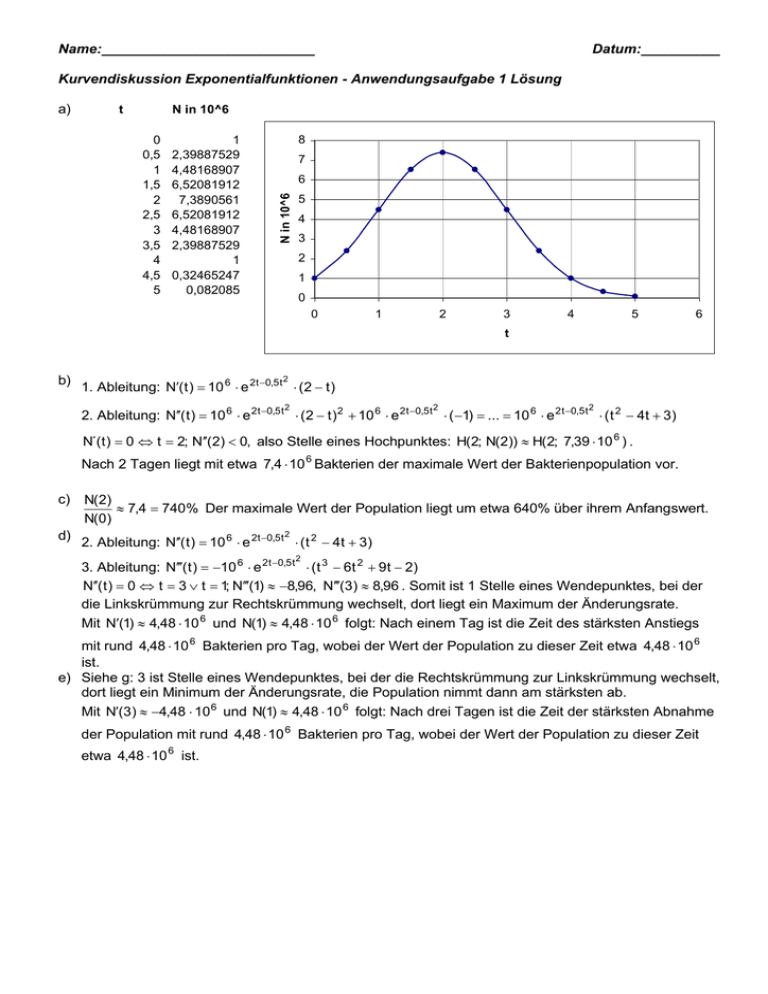
Name:___________________________
Datum:__________
Kurvendiskussion Exponentialfunktionen - Anwendungsaufgabe 1 Lösung
t
N in 10^6
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
1
2,39887529
4,48168907
6,52081912
7,3890561
6,52081912
4,48168907
2,39887529
1
0,32465247
0,082085
8
7
6
N in 10^6
a)
5
4
3
2
1
0
0
1
2
3
4
5
6
t
b)
2
1. Ableitung: N′( t ) = 10 6 ⋅ e 2 t −0,5 t ⋅ (2 − t )
2
2
2
2. Ableitung: N′′( t ) = 10 6 ⋅ e 2 t −0,5 t ⋅ (2 − t ) 2 + 10 6 ⋅ e 2 t −0,5 t ⋅ ( −1) = ... = 10 6 ⋅ e 2 t −0,5 t ⋅ ( t 2 − 4t + 3)
N´( t ) = 0 ⇔ t = 2; N′′(2) < 0, also Stelle eines Hochpunktes: H(2; N(2)) ≈ H(2; 7,39 ⋅ 10 6 ) .
Nach 2 Tagen liegt mit etwa 7,4 ⋅ 10 6 Bakterien der maximale Wert der Bakterienpopulation vor.
c) N(2)
≈ 7,4 = 740% Der maximale Wert der Population liegt um etwa 640% über ihrem Anfangswert.
N(0)
2
d)
2. Ableitung: N′′( t ) = 10 6 ⋅ e 2t −0,5 t ⋅ ( t 2 − 4t + 3)
2
3. Ableitung: N′′′( t ) = −10 6 ⋅ e 2 t −0,5 t ⋅ ( t 3 − 6t 2 + 9 t − 2)
N′′( t ) = 0 ⇔ t = 3 ∨ t = 1; N′′′(1) ≈ −8,96, N′′′(3) ≈ 8,96 . Somit ist 1 Stelle eines Wendepunktes, bei der
die Linkskrümmung zur Rechtskrümmung wechselt, dort liegt ein Maximum der Änderungsrate.
Mit N′(1) ≈ 4,48 ⋅ 10 6 und N(1) ≈ 4,48 ⋅ 10 6 folgt: Nach einem Tag ist die Zeit des stärksten Anstiegs
mit rund 4,48 ⋅ 10 6 Bakterien pro Tag, wobei der Wert der Population zu dieser Zeit etwa 4,48 ⋅ 10 6
ist.
e) Siehe g: 3 ist Stelle eines Wendepunktes, bei der die Rechtskrümmung zur Linkskrümmung wechselt,
dort liegt ein Minimum der Änderungsrate, die Population nimmt dann am stärksten ab.
Mit N′(3) ≈ −4,48 ⋅ 10 6 und N(1) ≈ 4,48 ⋅ 10 6 folgt: Nach drei Tagen ist die Zeit der stärksten Abnahme
der Population mit rund 4,48 ⋅ 10 6 Bakterien pro Tag, wobei der Wert der Population zu dieser Zeit
etwa 4,48 ⋅ 10 6 ist.
f)
Die Population wächst, während des ersten Tages sogar mit zunehmender Änderungsrate, danach
aber mit abnehmender Änderungsrate, von ihrem Anfangswert bis zu ihrem Maximum nach 2 Tagen,
fällt dann wieder ab, bis zum dritten Tag mit abnehmender Änderungsrate, dann aber wieder mit zunehmender Rate, und unterschreitet nach 4 Tagen ihren Anfangswert. Sie nähert sich dann rasch
dem Wert 0, erreicht ihn gemäß des mathematischen Modells jedoch erst im Unendlichen.
g) Die Giftmenge hat am Anfang den Wert 0 und steigt proportional mit der Zeit an. Die zu Anfang vorhandenen geringen Giftmengen stören die exponentielle Vermehrung kaum, die Population wächst
mit wachsender Änderungsrate. Die immer größer werdende Giftmenge töten aber irgendwann mehr
Bakterien, als von ihnen reproduziert werden, und dieser Anteil wächst dann mit fortschreitender Zeit
an, da weiterhin die Giftmenge erhöht wird.
h) N(10 ) = 10 6 ⋅ e −30 ≈ 9,4 ⋅ 10 −8 . N(10) ist also kleiner als1. Das Modell kann nur für solche Bakterienmengen sinnvolle Aussagen machen, die deutlich über 1 liegen, sodass die stufenähnliche Änderung der Population hinreichend gut durch die glatte Kurve des Modells angenähert wird: spätestens
bei N=1 versagt das Modell völlig. Die Beschreibung geringer Bakterienmengen ist aber auch nicht
die Intention des Modells.
i) Nach 2 Tagen sind die unmittelbaren Symptome, die durch die Infektion verursacht sind, wohl am
schlimmsten. Nach einem Tag verschlechtert sich der Zustand des Infizierten am schnellsten, und
nach drei Tagen verbessert sich der Zustand am schnellsten. Auf jeden Fall ist die Infektion nach 10
Tagen völlig abgeklungen.
ln
j)
2
2
N( t ) = 1 ⇔ 10 6 ⋅ e 2 t −0,5 t = 1 ⇔ e 2 t −0,5 t = 10 −6 ⇔ 2t − 0,5t 2 = ln(10 −6 ) ⇔ t 2 − 4t + 2 ⋅ ln(10 −6 ) = 0
⇔ t = 2 + 4 − 2 ⋅ ln(10 −6 ) ∨ t = 2 − 4 − 2 ⋅ ln(10 −6 ) . Die negative Zeit ist im Sinne der Sachaufgabe
144424443
144424443
≈ 7,62
≈ −3,62
unsinnig. Nach rund 7,62 Tagen ist – gemäß des Modells – die Population auf ein Bakterium gesunken.
k)
2
2
ln
N( t ) = 2 ⋅ 10 6 ⇔ 10 6 ⋅ e 2t −0,5 t = 2 ⋅ 10 6 ⇔ e 2t −0,5 t = 2 ⇔ 2t − 0,5t 2 = ln(2) ⇔ t 2 − 4t + 2 ⋅ ln(2) = 0
⇔ t = 2 + 4 − 2 ⋅ ln(2) ∨ t = 2 − 4 − 2 ⋅ ln( 2) . Nach rund 0,38 (etwa 9 h) Tagen und nach rund 3,62
144
42444
3
144
42444
3
≈ 0,383
≈ 3,617
Tagen (3 Tage und etwa 15 Stunden) liegen 200% der Anfangspopulation vor.
l)
N( t ) = 10 6 ⇔ 10 6 ⋅ e 2t −0,5 t = 10 6 ⇔ e 2 t −0,5 t = 1⇔ 2t − 0,5t 2 = 0 ⇔ t 2 − 4t = 0 ⇔ t ⋅ ( t − 4) = 0
⇔ t = 4 ∨ t = 0.
Nach 0 Tagen und nach 4 Tagen liegen 100% der Ausgangspopulation vor.
m)
N( t ) = 9 ⋅ 10 6 ⇔ 10 6 ⋅ e 2t −0,5 t = 9 ⋅ 10 6 ⇔ e 2t −0,5 t = 9 ⇔ 2t − 0,5t 2 = ln(9) ⇔ t 2 − 4t + 2 ⋅ ln(9) = 0
4 − 2 ln(9) < 0 : Somit hat die Gleichung keine Lösung, 900% des Anfangswertes werden nie erreicht.
Dies erkennt man auch am Graphen.
2
2
2
ln
2
ln