Mittelwertsatz der Differenzialrechnung

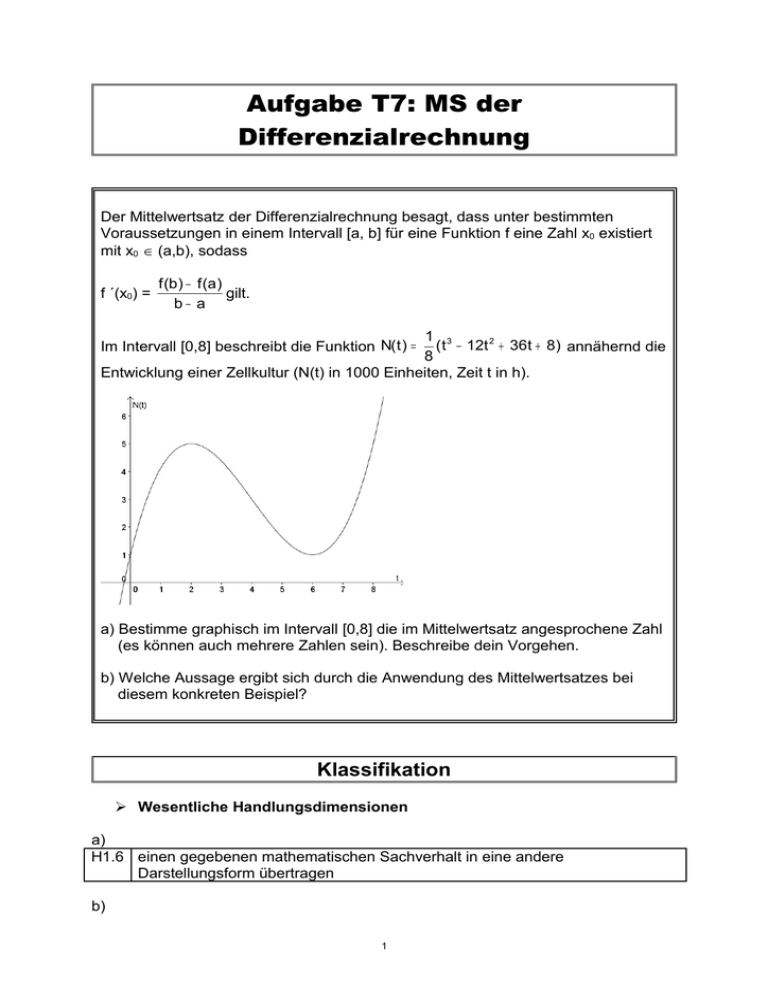
Aufgabe T7: MS der
Differenzialrechnung
Der Mittelwertsatz der Differenzialrechnung besagt, dass unter bestimmten
Voraussetzungen in einem Intervall [a, b] für eine Funktion f eine Zahl x0 existiert
mit x0 ∈ (a,b), sodass
f ´(x0) =
f (b) − f (a)
gilt.
b− a
1 3
( t − 12t 2 + 36t + 8) annähernd die
8
Entwicklung einer Zellkultur (N(t) in 1000 Einheiten, Zeit t in h).
Im Intervall [0,8] beschreibt die Funktion N( t ) =
a) Bestimme graphisch im Intervall [0,8] die im Mittelwertsatz angesprochene Zahl
(es können auch mehrere Zahlen sein). Beschreibe dein Vorgehen.
b) Welche Aussage ergibt sich durch die Anwendung des Mittelwertsatzes bei
diesem konkreten Beispiel?
Klassifikation
 Wesentliche Handlungsdimensionen
a)
H1.6 einen gegebenen mathematischen Sachverhalt in eine andere
Darstellungsform übertragen
b)
1
H3.4 mathematische Begriffe oder Sätze im jeweiligen Kontext deuten
2
 Wesentliche Inhaltsdimensionen
a) und b)
I 3.2 Differenzenquotient und Differentialquotient
 Komplexitätsdimension
a)
K1
Einsetzen von Grundkenntnissen
b)
K3
Reflektieren
 Nachhaltigkeit
N4
wieder holbar
Hilfsmittel
Keine Hilfsmittel
Gewohnte Hilfsmittel
Besondere Technologie erforderlich
J
Möglicher Lösungsweg
a)
Durch die Punkte A(0,1) und B(8,5) wird
eine Sekante gelegt. Der Anstieg der
Sekante bestimmt den Punkt P(xo,f(xo)
(und damit die Zahl xo), in welchem der
Anstieg der Tangente mit dem
Sekantenanstieg übereinstimmt.
P1(~1,7/~4,9) P(~6,3/~1,1)
b) mögliche Aussage:
In den ersten 8 Stunden ist die Zellkultur um durchschnittlich 500 Einheiten/h
(durchschnittliche Änderungsrate) gewachsen. Die momentane Änderungsrate
(momentane Wachstumsgeschwindigkeit) stimmt mit der durchschnittlichen
Änderungsrate zu den Zeitpunkten t1 ~ 1,7 h und t2 ~ 6,3 h überein.
3
Kommentar
Mit entsprechender Technologie kann auch die Berechnung verlangt werden.
ab Ende der 11. Schulstufe
 Technologieeinfluss
Regelmäßiger Technologieeinsatz im Unterricht ist:
vorteilhaft
neutral
nachteilig
erforderlich
4
J