Mittelwertsatz der Integralrechnung

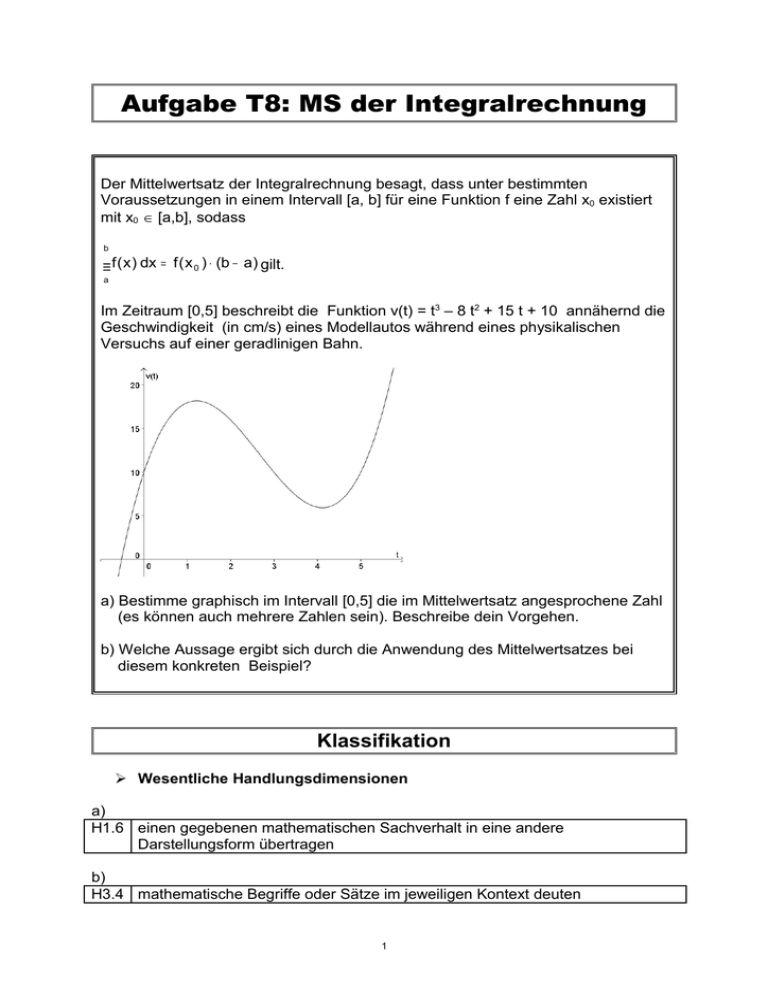
Aufgabe T8: MS der Integralrechnung
Der Mittelwertsatz der Integralrechnung besagt, dass unter bestimmten
Voraussetzungen in einem Intervall [a, b] für eine Funktion f eine Zahl x0 existiert
mit x0 ∈ [a,b], sodass
b
∫ f ( x ) dx =
f ( x 0 ) ⋅ (b − a) gilt.
a
Im Zeitraum [0,5] beschreibt die Funktion v(t) = t3 – 8 t2 + 15 t + 10 annähernd die
Geschwindigkeit (in cm/s) eines Modellautos während eines physikalischen
Versuchs auf einer geradlinigen Bahn.
a) Bestimme graphisch im Intervall [0,5] die im Mittelwertsatz angesprochene Zahl
(es können auch mehrere Zahlen sein). Beschreibe dein Vorgehen.
b) Welche Aussage ergibt sich durch die Anwendung des Mittelwertsatzes bei
diesem konkreten Beispiel?
Klassifikation
 Wesentliche Handlungsdimensionen
a)
H1.6 einen gegebenen mathematischen Sachverhalt in eine andere
Darstellungsform übertragen
b)
H3.4 mathematische Begriffe oder Sätze im jeweiligen Kontext deuten
1
 Wesentliche Inhaltsdimensionen
a) und b)
I 3.7 verschiedene Deutungen des bestimmten Integrals
 Komplexitätsdimension
a)
K1
Einsetzen von Grundkenntnissen
b)
K3
Reflektieren
 Nachhaltigkeit
N4
wieder holbar
Hilfsmittel
Keine Hilfsmittel
Gewohnte Hilfsmittel
Besondere Technologie erforderlich
J
Möglicher Lösungsweg
a)
Die Fläche zwischen dem Grafen der
Funktion, der x-Achse und der Vertikalen
x=5 kann in ein flächen-gleiches
Rechteck, dessen Seiten parallel zu den
Koordinatenachsen sind, verwandelt
werden.
Es ist darauf zu achten, dass im Intervall
[0,5] die von der Parallelen (zur x-Achse)
und dem oberhalb liegenden Grafen
eingeschlossenen Flächen mit der von
der Parallelen und dem unterhalb
liegenden Grafen eingeschlossenen
Flächen übereinstimmen. Daraus ergeben sich die Schnittpunkte (xo/f(xo) und damit
die Zahlen xo. P1(~0,15/~12,1) , P2(~2,66/~12,1) (rechnerische Werte)
b)
Die durch das Integral bestimmte Fläche kann als zurückgelegte Strecke des Autos
im Zeitraum [0,5] gedeutet werden. Es gibt nun nach dem Mittelwertsatz eine
konstante Geschwindigkeit, welche das Auto zu (mindestens) einem Zeitpunkt fährt,
sodass das Auto bei dieser Geschwindigkeit die gleiche Strecke zurücklegt.
Durchschnittsgeschwindigkeit: ca. 12,1 cm/s gefahren zu den Zeitpunkten t1=0,15 s
und t2 = 2,66 s
2
Kommentar
Mit entsprechender Technologie kann auch die Berechnung verlangt werden.
ab Ende der 12. Schulstufe
 Technologieeinfluss
Regelmäßiger Technologieeinsatz im Unterricht ist:
vorteilhaft
neutral
nachteilig
erforderlich
3
J