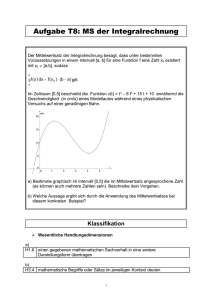
Lernzielkatalog "Integralrechnung"

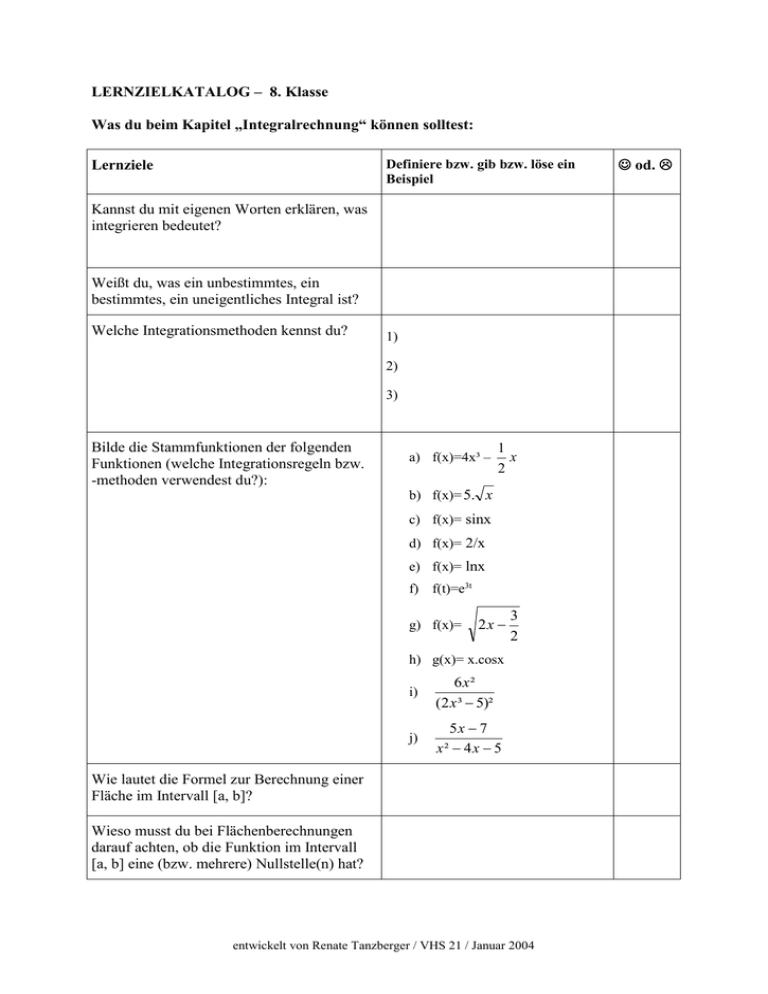
LERNZIELKATALOG – 8. Klasse
Was du beim Kapitel „Integralrechnung“ können solltest:
Definiere bzw. gib bzw. löse ein
Beispiel
Lernziele
Kannst du mit eigenen Worten erklären, was
integrieren bedeutet?
Weißt du, was ein unbestimmtes, ein
bestimmtes, ein uneigentliches Integral ist?
Welche Integrationsmethoden kennst du?
1)
2)
3)
Bilde die Stammfunktionen der folgenden
Funktionen (welche Integrationsregeln bzw.
-methoden verwendest du?):
a) f(x)=4x³ –
1
x
2
b) f(x)= 5. x
c) f(x)= sinx
d) f(x)= 2/x
e) f(x)= lnx
f) f(t)=e3t
g) f(x)=
2x 
3
2
h) g(x)= x.cosx
i)
6 x²
(2 x ³  5)²
j)
5x  7
x²  4 x  5
Wie lautet die Formel zur Berechnung einer
Fläche im Intervall [a, b]?
Wieso musst du bei Flächenberechnungen
darauf achten, ob die Funktion im Intervall
[a, b] eine (bzw. mehrere) Nullstelle(n) hat?
entwickelt von Renate Tanzberger / VHS 21 / Januar 2004
 od. 
Was du beim Kapitel „Integralrechnung“ können solltest:
Kannst du Flächen zwischen Kurve und xAchse bzw. zwischen zwei Kurven
berechnen?
Bsp. 1: Berechne die Fläche zwischen
f(x)=x³-9x²+18x und der x-Achse.
Wie lautet die Formel zur Berechnung des
Volumens einer um die x-Achse rotierenden
Fläche im Intervall [a, b]?
Bsp.: Das Flächenstück, das von
Bsp. 2: Berechne das von f(x)=-x²/6
und g(x)=-x³/3 + x eingeschlossene
Flächenstück!
f: y²=8x und g: y=
2
8
x  begrenzt
3
3
wird, rotiert um die x-Achse. Berechne
das Volumen des Rotationskörpers.
Wie lautet die Formel zur Berechnung des
Volumens einer um die y-Achse rotierenden
Fläche im Intervall [c, d]?
Geg.: f(x)=0,5x²+1 rotiert in [1;3] um
die y-Achse. Berechne das dadurch
entstehende Volumen.
Wie lautet die Formel zur Berechnung der
Länge eines Kurvenbogens (=Bogenlänge
einer Kurve) im Intervall [a, b]?
Berechne die Länge der Schleife der
Kurve mit der Gleichung:
9y²=x.(3-x)² !
Wie lautet die Formel zur Berechnung eines
Schwerpunktes einer Fläche?
Berechne den Schwerpunkt der Fläche
des Graphen von y=x/2+4 in [-8;0] !
Wie lautet die Formel zur Berechnung eines
Schwerpunktes eines Körpers, der durch
Drehung einer Fläche um die x-Achse
entsteht?
Das Flächenstück, das von der Hyperbel: x²-y²=9 und den Geraden g1: x=0
und g2: x=6 begrenzt wird, rotiert um
die x-Achse. Berechne den Schwerpunkt des Körpers, der dadurch
entsteht.
Kannst du auch komplizierte Beispiele lösen? Bsp. 1: Eine Parabel 3.Ordnung hat im
Punkt (0/0) die Steigung k=0 und in
W(1/y) einen Wendepunkt. Der Graph
schließt mit der x-Achse eine Fläche
von 20,25AE ein. Wie lautet die
Parabel?
Bsp. 2: f (x)=x³ -3x²+4
a) Berechne die von f (x) und der xAchse eingeschlossene Fläche!
b) Die Graphen von f (x) und
g(x) =x+1 schließen zwei Flächen ein.
Weise nach, dass die beiden Flächen
gleich groß sind!
c) In das Dreieck, welches die Wendetangente mit den Koordinatenachsen
bildet, soll ein möglichst großes
Rechteck einbeschrieben werden. Für
welchen x-Wert geschieht das?
entwickelt von Renate Tanzberger / VHS 21 / Januar 2004