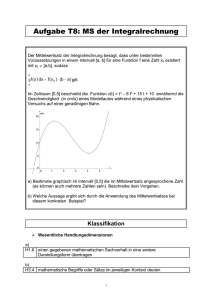
X n 0 5 p , = n σ X n

Kurs 13ma2
Konfidenzintervalle 1
27.11.2008
Aufgabe 1:
Bei einer Meinungsumfrage zur Beliebtheit von Politikern wird eine repräsentative Stichprobe
der Bevölkerung befragt. Da die Mitwirkung der Betroffenen freiwillig ist, wird angenommen,
dass nur 65% der Befragten antworten werden.
Es werden 3000 Personen zur Befragung vorgesehen. Mit wie vielen Antworten kann
gerechnet werden (Sicherheitswahrscheinlichkeit 90%)?
Aufgabe 2:
Tulpenzwiebeln einer bestimmten Sorte lassen sich zu 80% erfolgreich anpflanzen.
a) Eine Gärtnerei bezieht 10000 Stück. Wie viele Tulpen stehen zum Verkauf zur
Verfügung (99 % Sicherheitswahrscheinlichkeit) ?
b) An Privatpersonen werden die Tulpenzwiebeln in Packungen zu 100 Stück
abgegeben. Welche Mindestgarantie kann auf 90% Sicherheitsniveau gegeben
werden?
Rückbesinnung: Erkläre den Unterschied zwischen Wahrscheinlichkeit, relativer
Häufigkeit und absoluter Häufigkeit.
Bisher haben wir absolute Häufigkeiten geschätzt. Es wurden Abweichungen der absoluten
trefferzahl X (Zufallsvariable) in einer Bernoulli-Kette der Länge n vom Erwartungswert μ
untersucht. Nun wollen wir uns mit der Schätzung von relativen Häufigkeiten befassen. Es
X
von der Trefferwahrscheinn
lichkeit p , also letztendlich um eine Schätzung der unbekannten Wahrscheinlichkeit p .
geht also um Abweichungen der relativen Trefferhäufigkeit
Wahrscheinlichkeiten
von
Die Werte von
σ
-Umgebungen
n
X
fallen zu etwa
n
σ
σ⎤
⎡
90% ins Intervall ⎢ p − 1,64 ⋅ ; p + 1, 64 ⋅ ⎥
n
n⎦
⎣
σ
σ⎤
⎡
95% ins Intervall ⎢ p − 1,96 ⋅ ; p + 1,96 ⋅ ⎥
n
n⎦
⎣
σ
σ⎤
⎡
99% ins Intervall ⎢ p − 2,58 ⋅ ; p + 2,58 ⋅ ⎥
n
n⎦
⎣
Aufgabe 3:
Eine Münze wird 1000-mal geworfen. Prognostiziere mit einer Sicherheitswahrscheinlichkeit
von 95% in welches Intervall um den erwarteten Wert p = 0 ,5 die relative Häufigkeit für
„Kopf“ fallen wird.