Differenzenquotient

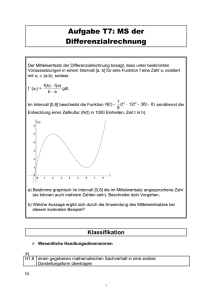
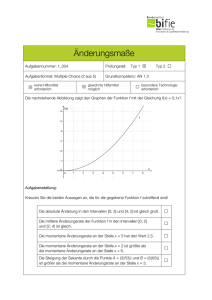
Der Differenzenqoutienten
1. Einheit:
Die mittlere Geschwindigkeit
Beispiel 1) Durchschnittsgeschwindigkeiten eines Zuges
Die untenstehende Tabelle ist ein Auszug aus dem Fahrplan des Railjet von Zürich nach
Budapest.
an/arr
ab /dep
Bahnhof / station
km
10:40
Zürich
...
...
...
...
...
18:48
Wien Westbahnhof
...
19:01
19:03
Wien Meidling
4
19:56
19:58
Hegyeshalom
76
20:03
20:05
Mosonmagyarowar
11
20:23
20:25
Györ
36
Budapest
125
21:54
a) Berechne die mittlere Geschwindikeit des Zuges zwischen Wien Westbahnhof und
Wien Meidling, Wien Meidling und Hegyeshalom, Hegyeshalom und Mosonmagyarowar,
Mosonmagyarowar und Györ sowie Györ und Budapest.


In welchem der Streckenabschnitte fährt der Zug im Mittel am schnellsten?
In welchem der Streckenabschnitte fährt der Zug im Mittel am langsamsten?
b) Die Bewegung des Zuges werde durch die Zeit- Ort – Funktion s: t → s(t) beschrieben.
Gib eine Formel für die mittlere Geschwindigkeit v(t 1, t2) des Zuges im Zeitintervall
[t1;t2] an.
Merke:
Ein Körper bewege sich gemäß der Zeit – Ort – Funktion s: t → s(t). Man nennt
v t1 , t2 =
s t2 − s t 1
t2 − t1
die mittlere Geschwindigkeit des Körpers im Zeitintervall [t1;t2].
Die mittlere Änderungsrate
Beispiel 2) Mittlere Temperaturänderungen
In der untenstehenden Tabelle sind zu verschiedenen Uhrzeiten t eines Tages,
gemessene Temperaturen T(t) an einem bestimmten Ort angegeben.
Uhrzeit t
Temperatur T(t) in °C
9
10
12
13
14
17
a) Berechne die Temperaturzunahme im Zeitintervall [9;12] bzw. [12;14].
b) Gib die Temperaturzunahme im Zeitintervall [t1; t2] an.
c) Berechne die mittlere Temperaturzunahme pro Stunde im Zeitintervall [9;12] bzw.
[12;14]. In welchem dieser Zeitintervalle nimmt die Temperatur im Mittel schneller zu?
d) Gib die mittlere Temperaturzunahme pro Stunde im Zeitintervall [t 1; t2] an.
s t 2 − s t1
t2 − t 1
T t 2 − T t1
t2 − t1
Ausdrücke der Form
oder
bezeichnet man als
Differenzenqoutienten oder mittlere Änderungsraten. Allgemein definiert man:
Definition:
Es sei f: A → ℝ eine reelle Funktion und [a; b] ⊆ A . Dann heißt die reelle Zahl
f b − f a
der Differenzenquotient oder die mittlere Änderungsrate
b− a
von f in [a; b].
Beispiel 3) Quatratische Funktion
Gegeben sei die Funktion f mit f(x) = ½ . (x – 2)².
Berechne den Differenzenquotienten im Intervall
a) [0;1]
b) [2;4]
c) [0;4]
Beispiel 4)
Gib den Differenzenqoutienten der nachstehenden Funktion im angegebenen Intervall
an.
a) r → A(r), [r1;r2]
b) z → F(z), [z1; z2]
c) y → T(y), [c-h; c]
Beispiel 5)
Gib Termdarstellungen von 3 verschiedenen Funktionen an, deren Differnezenquotient
im Intervall [0;1] genau 1 beträgt. Skizziere die Graphen dieser Funktionen.
Hausübung: Aufgaben 3, 5d, 8c, 10 (vom Übungsblatt)
2. Einheit:
Die mittlere Änderungsrate in der Geometrie
Beispiel 5) Aufblasen eines Ballons
Ein kugelförmiger Ballon vom Radius r hat das Volumen V(r) = 4∏r³/3 (r in cm, V in cm³).
Der Ballon wird aufgeblasen.
a) Berechne die Volumenszunahme im Radiusintervall
[5;6] bzw. [20;20,1]. (Zuvor: Schätzen in welchem
Fall die Volumszunahme größer ist.)
b) Gib die Volumszunahme im Radiusintervall [r1; r2]
an
c) Berechne die mittlere Volumszunahme pro cm
Radius in den Radiusintervallen [5;6] und [20;20,1].
In welchem dieser Intervalle ist die mittlere
Volumszunahme pro cm Radius größer?
d) Gib die mittlere Volumszunahme pro cm Radius im
Radiusintervall [r1; r2] an.
Vorzeichen des Differenzenquotienten
Was sagt das Vorzeichen eines Differenzenqoutienten aus?
Ist [a,b] ein Intervall, dann gilt b – a > 0 und es folgt:

f b − f a
b− a
>0
→f(b) – f(a) > 0 →f(a) < f(b)

f b − f a
b− a
<0
→f(b) – f(a) < 0 →f(a) > f(b)

f b − f a
b− a
=0
→f(b) – f(a) = 0 →f(a) = f(b)
Ist der Differenzenqoutient von f in [a;b]

positiv, so sagt man, f steigt insgesamt (im Mittel) in [a; b].
(Die Funktion f muss aber nicht monoton steigend in [a;b] sein.)

negativ, so sagt man, f fällt insgesamt (im Mittel) in [a; b].
(Die Funktion f muss aber nicht monoton fallend in [a;b] sein.)

gleich 0, so bedeutet dies, dass f an der Stelle a und b den gleichen Wert
annimmt. (Die Funktion f muss aber konstant in [a;b] sein.)
Beispiel 6)
Gegeben ist die nebenstehend abgebildete
Funktion f.
Stelle ohne zu rechnen fest, in welchen der
Intervalle [0;2], [2;4], [0,6] und [5;8] der
Differenzenquotient von f positiv, in welchen
negativ und in welchen gleich 0 ist.
Beispiel 7)
Zeichne die Graphen zweier verschiedener Funktionen im Intervall [1;8], die beide in
[1;3] die mittlere Änderungsrate -1, in [3;5] den Differenzenquotienten 2 und in [5;8]
die mittlere Änderungsrate 0 haben.
Differenzenquotient als Steigung der Sekantenfunktion
Beispiel 8)
Berechne den Differenzenqoutienten einer linearen Funktion f mit f(x) = k.x + d in einem
intervall [a;b].
Aus dieser Aufgabe ergibt sich:
Satz:
Der Differenzenquotient (die mittlere Änderungsrate) einer linearen Funktion f mit
f(x) = k.x + d ist in jedem Intervall [a; b] gleich der Steigung k.
Ist f in [a; b] nicht linear, so kann man die lineare
Funktion s mit s(a) = f(a) und s(b) = f(b)
betrachten.
(siehe nebenstehende Abbildung)
Man nennt diese Funktion die Sekantenfunktion
von f in [a; b].
Der Graph von f verläuft oft in der Nähe des
Graphen von s. Dies muss aber nicht immer der Fall
sein.
Ist k die Steigung der linearen Sekantenfunktion s, dann gilt aufgrund des obigen Satzes:
f b − f a
s b − s a
=
= k
b− a
b− a
Es gilt also:
Satz:
Der Differenzenquotient (die mittlere Änderungsrate) einer Funktion f in [a; b] ist
glöeich der Steigung der Sekantenfunktion von f in [a; b].
Beispiel 9)
Sei f(x) = x². Ermittle z > 1 so, dass die Steigungd der Sekantenfunktion von f im
Intervall [1; z] gleich 3 ist.
Hausübung: Aufgaben 14, 18, 19, 21b (vom Übungsblatt)