Aufgaben - Markgräfin-Wilhelmine

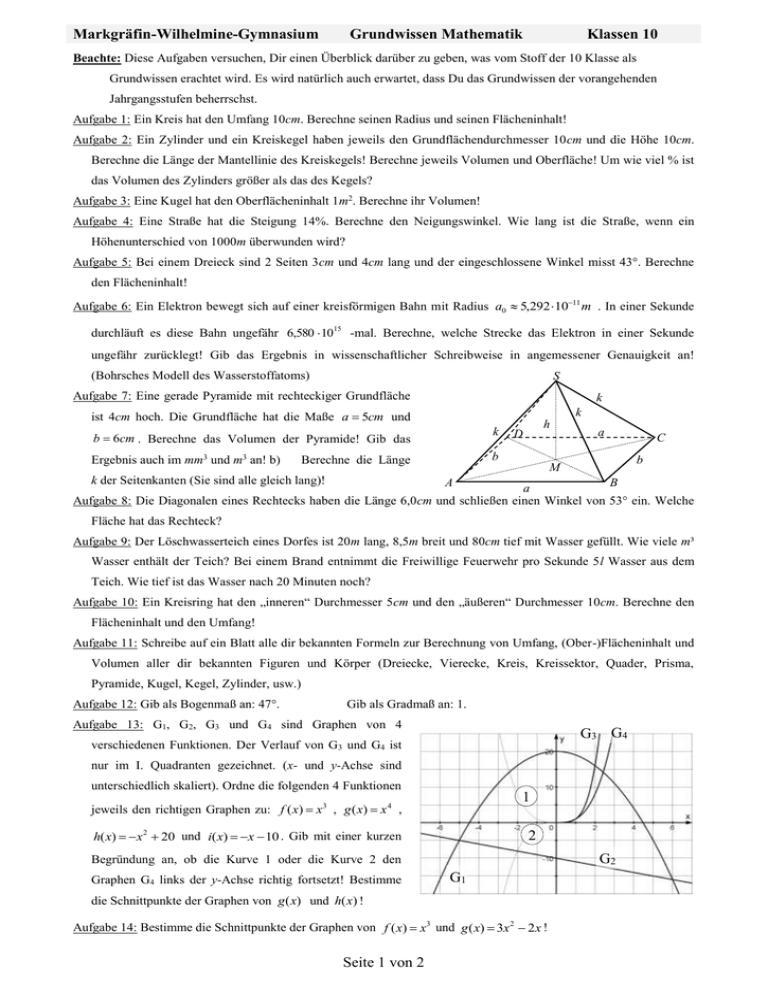
Markgräfin-Wilhelmine-Gymnasium
Grundwissen Mathematik
Klassen 10
Beachte: Diese Aufgaben versuchen, Dir einen Überblick darüber zu geben, was vom Stoff der 10 Klasse als
Grundwissen erachtet wird. Es wird natürlich auch erwartet, dass Du das Grundwissen der vorangehenden
Jahrgangsstufen beherrschst.
Aufgabe 1: Ein Kreis hat den Umfang 10cm. Berechne seinen Radius und seinen Flächeninhalt!
Aufgabe 2: Ein Zylinder und ein Kreiskegel haben jeweils den Grundflächendurchmesser 10cm und die Höhe 10cm.
Berechne die Länge der Mantellinie des Kreiskegels! Berechne jeweils Volumen und Oberfläche! Um wie viel % ist
das Volumen des Zylinders größer als das des Kegels?
Aufgabe 3: Eine Kugel hat den Oberflächeninhalt 1m2. Berechne ihr Volumen!
Aufgabe 4: Eine Straße hat die Steigung 14%. Berechne den Neigungswinkel. Wie lang ist die Straße, wenn ein
Höhenunterschied von 1000m überwunden wird?
Aufgabe 5: Bei einem Dreieck sind 2 Seiten 3cm und 4cm lang und der eingeschlossene Winkel misst 43°. Berechne
den Flächeninhalt!
Aufgabe 6: Ein Elektron bewegt sich auf einer kreisförmigen Bahn mit Radius a0  5,292  1011 m . In einer Sekunde
durchläuft es diese Bahn ungefähr 6,580  1015 -mal. Berechne, welche Strecke das Elektron in einer Sekunde
ungefähr zurücklegt! Gib das Ergebnis in wissenschaftlicher Schreibweise in angemessener Genauigkeit an!
(Bohrsches Modell des Wasserstoffatoms)
S
Aufgabe 7: Eine gerade Pyramide mit rechteckiger Grundfläche
k
k
ist 4cm hoch. Die Grundfläche hat die Maße a  5cm und
b  6cm . Berechne das Volumen der Pyramide! Gib das
k
Ergebnis auch im mm3 und m3 an! b)
b
Berechne die Länge
h
D
a
C
b
M
k der Seitenkanten (Sie sind alle gleich lang)!
A
B
a
Aufgabe 8: Die Diagonalen eines Rechtecks haben die Länge 6,0cm und schließen einen Winkel von 53° ein. Welche
Fläche hat das Rechteck?
Aufgabe 9: Der Löschwasserteich eines Dorfes ist 20m lang, 8,5m breit und 80cm tief mit Wasser gefüllt. Wie viele m³
Wasser enthält der Teich? Bei einem Brand entnimmt die Freiwillige Feuerwehr pro Sekunde 5l Wasser aus dem
Teich. Wie tief ist das Wasser nach 20 Minuten noch?
Aufgabe 10: Ein Kreisring hat den „inneren“ Durchmesser 5cm und den „äußeren“ Durchmesser 10cm. Berechne den
Flächeninhalt und den Umfang!
Aufgabe 11: Schreibe auf ein Blatt alle dir bekannten Formeln zur Berechnung von Umfang, (Ober-)Flächeninhalt und
Volumen aller dir bekannten Figuren und Körper (Dreiecke, Vierecke, Kreis, Kreissektor, Quader, Prisma,
Pyramide, Kugel, Kegel, Zylinder, usw.)
Aufgabe 12: Gib als Bogenmaß an: 47°.
Gib als Gradmaß an: 1.
Aufgabe 13: G1, G2, G3 und G4 sind Graphen von 4
G3 G4
verschiedenen Funktionen. Der Verlauf von G3 und G4 ist
nur im I. Quadranten gezeichnet. (x- und y-Achse sind
unterschiedlich skaliert). Ordne die folgenden 4 Funktionen
1
jeweils den richtigen Graphen zu: f ( x)  x3 , g ( x)  x 4 ,
h( x)   x 2  20 und i( x)  x  10 . Gib mit einer kurzen
2
G2
Begründung an, ob die Kurve 1 oder die Kurve 2 den
Graphen G4 links der y-Achse richtig fortsetzt! Bestimme
G1
die Schnittpunkte der Graphen von g (x) und h(x) !
Aufgabe 14: Bestimme die Schnittpunkte der Graphen von f ( x)  x3 und g ( x)  3x 2  2 x !
Seite 1 von 2
Markgräfin-Wilhelmine-Gymnasium
Grundwissen Mathematik
Klassen 10
Aufgabe 15: In nebenstehendem Diagramm sind 4 Graphen
3
4
4
eingezeichnet.
Gib jeweils die zugehörige Funktionsgleichung an!
Berechne die Schnittpunkte der Graphen der Funktionen
1
1
2
7
f ( x)  und g ( x)   x  !
x
3
3
1
f ( x)  4x2  4x  8 und
Aufgabe 16: Gegeben sind die Funktionen
g ( x)  4x  4 .
Bestimme
y-Achsenabschnitt,
Nullstellen
2
und
Scheitelkoordinaten von Gf ! Bestimme die Schnittpunkte von Gf und Gg!
Aufgabe 17: Faktorisiere so weit möglich und gib die Achsenpunkte an: f ( x)  x3  4x2  7 x  10 !
Aufgabe 18: Aus einem Zylinder mit Radius r  7cm und Höhe h  10cm wurde ein
halbkugelförmiges Loch gebohrt (siehe Skizze). Berechne die Oberfläche A und das Volumen V
des entstandenen Körpers!
( x6  5x5  2x 4  x 2  3x  12) : ( x3  x 2  2x  1) 
Aufgabe 19: Führe eine Polynomdivision durch:
Aufgabe 20: In einer deutschen Stadt gab es im Jahr 1991 ungefähr 14 000 Handy-Besitzer. Seither ist die Zahl jährlich
um 30% gestiegen. Wie viele Handy-Besitzer gab es im Jahr 2002? Runde sinnvoll! Um wie viel Prozent ist ihre
Zahl in dem Zeitraum gestiegen? Bestimme den Funktionsterm , der die Zahl der Handy-Besitzer in Abhängigkeit
von den seit 1991 vergangenen Jahren angibt! Zeichne den Graphen für die auf 1991 folgenden 5 Jahre!
Aufgabe 21: Ein zylinderförmiges Gefäß mit dem Grundflächenradius 4cm ist teilweise mit Wasser gefüllt. Der
Wasserspiegel steigt um 5cm, wenn man 6 Stahlkugeln (ganz) eintaucht. Bestimme den Durchmesser der Kugeln!
Aufgabe 22: Bestimme den Scheitel der Funktion f ( x)  2( x  3)(x  5) !
Aufgabe 23: Um wie viel Prozent ist der Flächeninhalt eines Quadrats mit Seitenlänge 2,5m größer als derjenige eines
Quadrats mit Seitenlänge 2m?
2
 3a 2b  a 4b 3
 2  :
 2 x y  12 xy 2 ;


2s  1
3
 3 ;
Aufgabe 24: Fasse jeweils zusammen:
4
s
2s
2
a
4( )  4 ( ) 2 ;
a
4
a 7b16 a 9 ;
 (12 y 2 z )5 : (
4
3 y 5
) ;
4 x2
x5  x

3
4
x 7 y16
;
y9
4
(x 5 )
;

3
4
 (12 b 2c)5 : (
3 b 5
) ;
4 a2
1
1
 ;
x 1 x
;
a3 a ;
1 2
a  2a 9,5  3a 0,5 ;
6
Aufgabe 25: Berechne (falls nötig mit dem TR):
7
2187 ;
9
4
3,63, 7 ;
81 ;
5
1,4  1017
;
2,9  10 7
2,34  42,3 ;
( x  1)3  ( x  1)2  0 ;
1
2;
x 1
(3) 4 ;
58
( x  3)
Aufgabe 26: Bestimme jeweils die Lösungsmenge:
4
4

1 ;
x 1 x 1
1
1
 ;
x 1 x

3
4
 13 ;
5
3  72 x  5  7 x  2 ;
log10 ( x  4)  log10 x  log10 3 ;
x4  4x2  5 ;
Aufgabe 27: Zerlege so weit wie möglich: log s
9 17
;
53  11
Aufgabe 28: Fasse so weit wie möglich zusammen:
log a
23  25
7  11
log b 3  2 log b 5 ;
Seite 2 von 2
;
2 log 3 6  log 3 4 ;
2
(3152  x 2 ) 3  9 ;