Kapitel 33 Grundlagen der elektromagnetischen Wellen

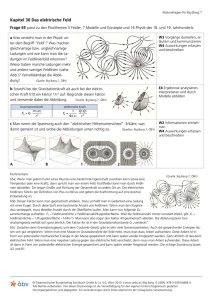
Maturafragen für Big Bang 7
Kapitel 33 Grundlagen der elektromagnetischen Wellen
Frage 71 passt zu den Poolthemen 5 Felder, 7 Modelle und Konzepte, 12 Paradigmenwechsel in der Physik/Entwicklung der Weltbilder, 16 Physik des 18. und 19. Jahrhunderts, 21 Physik und Technik, 22 Schwingungen und Wellen, 23
Strahlung und 25 Vereinheitlichungen in der Physik
W1 Vorgänge beschreiben
und benennen
W2 Informationen entnehmen
a Man sagt, eine Welle ist die Ausbreitung einer Störung. Was ist damit gemeint? Gib Beispiele zur Entstehung von Wellen an. Was wird bei der Entstehung einer elektromagnetischen Welle gestört? Verwende für deine Erklärung
die Abbildung!
(Quelle: Big Bang 7, ÖBV)
b Das System Aldis (Austrian Lightning Detection and Information System) erfasst alle Blitze in Österreich. Wie könnte es vereinfacht gesagt funktionieren? Überlege mit Hilfe der
Antwort zu a.
E2 Fragen stellen und Vermutungen aufstellen
c In manchen Physikbüchern gibt
es kein Kapitel „Optik“, obwohl
die Physik des Lichts sehr wohl besprochen wird. Unter welchem Kapitel muss man in diesem Fall nachschlagen? Erkläre in diesem Zusammenhang die Abbildung!
E4 Ergebnisse analysieren,
interpretieren und durch
Modelle abbilden
(Quelle: Big Bang 7, ÖBV)
W3 Vorgänge darstellen, erläutern und kommunizieren
d MAXWELL konnte berechnen, dass sich die von ihm gefundenen EM-Wellen mit der Geschwindigkeit = 1/
∙ µ ausbreiten. Für die elektrische Feldkonstante gilt
ε 0 = 8,854187817∙10-12 As/Vm und für die magnetische Feldkonstante gilt
µ 0 = 4∙π∙10-7 Vs/Am. 1) Berechne daraus die Lichtgeschwindigkeit und vergleiche mit dem
Wert 299.792.458 m/s. 2) Überprüfe die Einheit von c.
Kommentare
71a: Bei einer Flüssigkeitswelle wird z. B. die ruhende Wasseroberfläche gestört. Beim Donner wird die ruhende Luft durch die plötzliche
Ausdehnung der Luft im Blitzkanal gestört. Bei einer elektromagnetischen Welle wird das elektrische Feld durch die Beschleunigung einer
Ladung gestört. Um eine elektromagnetische Welle auszulösen, muss das elektrische Feld gestört werden! Die Feldlinien in Abb. a zeigen
radial nach außen und geben Information darüber, wo sich die Ladung befindet. Nun wird die Ladung nach oben wegbewegt, also beschleunigt (b und c). Die Information über diese Bewegung kann sich aber nur mit Lichtgeschwindigkeit ausbreiten. Daher „wissen“ außerhalb eines kreisförmigen, sich mit Lichtgeschwindigkeit ausbreitenden Bereichs die Feldlinien noch nichts von der Bewegung der Ladung,
wodurch ein Knick entsteht. Das ist die Störung. Ein veränderliches elektrisches Feld erzeugt aber ein magnetisches Feld und ein veränderliches magnetisches Feld erzeugt ein elektrisches Feld. Das erklärt, warum der vorbeilaufende Knick des elektrischen Feldes auch eine magnetische Komponente besitzt.
71b: Elektromagnetische Pulse (EMPs) werden durch beschleunigte Ladungen ausgelöst. Vor einem Blitz sind die Ladungen in Ruhe, während des Blitzes fließen sie. Die Beschleunigung der Ladungen löst einen EMP aus, der von ALDIS gemessen werden kann.
71c: Die Entdeckungen von ØRSTED und MAXWELL vereinigten Elektrizität, Magnetismus und Licht zum Elektromagnetismus. Unter diesem
Kapitel muss man in manchen Büchern nachschlagen, um die Optik zu finden.
71d: Durch Einsetzen der Werte erhält man für c den Wert 299.792.458 m/s, was natürlich genau der Definition der Lichtgeschwindigkeit
entsprechen muss. Für die Berechnung der Einheit der Lichtgeschwindigkeit gilt
=
∙
=
∙
=
= .
© Österreichischer Bundesverlag Schulbuch GmbH & Co. KG, Wien 2010. | www.oebv.at | Big Bang 6 | ISBN: 978-3-209-04868-4
Alle Rechte vorbehalten. Von dieser Druckvorlage ist die Vervielfältigung für den eigenen Unterrichtsgebrauch gestattet.
Die Kopiergebühren sind abgegolten. Für Veränderungen durch Dritte übernimmt der Verlag keine Verantwortung.
Maturafragen für Big Bang 7
Kapitel 33 Grundlagen der elektromagnetischen Wellen
Frage 72 passt zu den Poolthemen 5 Felder, 6 Information und Kommunikation, 7 Modelle und Konzepte, 16 Physik
des 18. und 19. Jahrhunderts, 18 Physik und Alltag, 21 Physik und Technik, 22 Schwingungen und Wellen, 23 Strahlung und 25 Vereinheitlichungen in der Physik
a Erkläre mit Hilfe der Abbildung, wie ein Schwingkreis funktioniert. Ziehe dabei auch eine
Analogie zu einem schwingenden Pendel.
W1 Vorgänge beschreiben
und benennen
W2 Informationen entnehmen
(Quelle: Big Bang 7, ÖBV)
b Erkläre in Zusammenhang mit Frage a den Begriff Rückkopplung. In welchem Zusammenhang steht dabei die Abbildung?
W1 Vorgänge beschreiben
und benennen
E2 Fragen stellen und Vermutungen aufstellen
(Quelle: Big Bang 7, ÖBV)
c Wie lang muss eine Sendeantenne sein, damit man damit den Musiksender Ö3
mit 99,9 MHz übertragen kann? Verwende dazu die Gleichung c = λ∙f. c ist die
Lichtgeschwindigkeit (rund 3∙108 m/s) und f die Frequenz des Senders. Erkläre in
diesem Zusammenhang den Begriff „λ/2-Dipol“.
W3 Vorgänge darstellen, erläutern und kommunizieren
(Quelle: Wikipedia)
d Radios können, ohne dass man die Länge der Antenne
verändert, alle FM-Sender gut empfangen. Warum ist das
in der Praxis wichtig? Überlege, was das für die Dämpfung des Empfängerschwingkreises bedeutet.
E4 Ergebnisse analysieren,
interpretieren und durch
Modelle abbilden
Zusammenhang zwischen Anregungsfrequenz und Amplitude der
Schwingung bei verschieden starken Dämpfungen (a = schwache
Dämpfung, d = starke Dämpfung; Quelle: Big Bang 7, ÖBV)
Kommentare
72a: Der Kondensator wird aufgeladen (a) und dann entladen. Durch den Stromfluss baut sich in der Spule ein Magnetfeld auf (b). Wenn
der Kondensator entladen ist, bricht das Magnetfeld zusammen. Dadurch kommt es in der Spule zur Selbstinduktion, die den Stromfluss
noch aufrechterhält, wodurch sich der Kondensator gegengleich auflädt (c). Dann läuft alles wieder retour (d + a) und fängt von neuem an.
Nicht nur die Ladungen schwingen, sondern auch die Energie. Ähnlich ist es bei einem schwingenden Pendel. Dort wandeln sich potenzielle
und kinetische Energie ineinander um.
72b: Wenn man ein Pendel nur einmal anstupst, dann wird es bald auspendeln (gedämpfte Schwingung). Wenn man aber im richtigen
Zeitpunkt Energie zuführt, indem man am höchsten Punkt antaucht, kann man eine ungedämpfte Schwingung erzeugen. Beim Schwingkreis übernimmt eine elektronische Schaltung das „Antauchen“ (Rückkopplung).
72c: Es gilt λ = c/f und daher λ/2 = c /(2f ). Die Sendeantenne für Ö3 muss daher 3∙108/(199,8∙106) m ≈ 1,5 m lang sein. Weil sich die Enden
der Antenne wie die Platten des Kondensators wechselweise unterschiedlich laden, sagt man zu ihr auch Dipol! Die Stromstärke in der Mitte
der Antenne hat einen Schwingungsbauch (maximale Amplitude) und ist am Rand null (Amplitude null). Das ist die Grundschwingung einer
stehenden Welle. Die Länge dieser Grundschwingung entspricht der halben Wellenlänge (λ/2) der fortschreitenden elektromagnetischen
Welle, und daher kommt die Bezeichnung „λ/2-Dipol“.
72d: Wenn man leicht unterschiedliche Frequenzen gut empfangen möchte, damit man die Antenne nicht ständig verändern muss, darf ihr
Resonanzverhalten nicht scharf ausgeprägt sein. Der Abbildung kann man entnehmen, dass in diesem Fall die Dämpfung stärker sein muss
(c+d), die Schwingung würde also unangeregt schnell wieder auspendeln.
© Österreichischer Bundesverlag Schulbuch GmbH & Co. KG, Wien 2010. | www.oebv.at | Big Bang 6 | ISBN: 978-3-209-04868-4
Alle Rechte vorbehalten. Von dieser Druckvorlage ist die Vervielfältigung für den eigenen Unterrichtsgebrauch gestattet.
Die Kopiergebühren sind abgegolten. Für Veränderungen durch Dritte übernimmt der Verlag keine Verantwortung.