Blatt 4

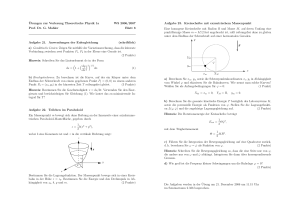
TP1: Mechanik
Arbeitsblatt 4
Sommersemester 2015
19/20.05.2015
Dynamik und Erhaltungsgrößen
Auf diesem Blatt behandeln wir die Dynamik und Erhaltungsgrößen physikalischer Systeme. Mit
deren Hilfe können wesentliche Ergebnisse über physikalische Zusammenhänge erziehlt werden.
Aufgabe 13: Das ballistische Pendel
Die Geschwindigkeit einer Gewehrkugel kann mit Hilfe eines ballistischen Pendels gemessen werden. Dieses besteht aus einem Faden, dessen Gewicht wir vernachlässigen können, und einer Masse
mG , die an dem Faden befestigt ist. Nun wird die Gewehrkugel in den Klotz geschossen und bleibt
stecken. Man misst die Bogenlänge, die von der Masse mG zurückgelegt wird. Folgende Skizze
veranschaulicht das ballistische Pendel:
a) Bestimmen Sie die Geschwindigkeit des Klotzes und die gesamte kinetische Energie des
Systems nach dem Stoß.
b) Bestimmen Sie die Geschwindigkeit der Gewehrkugel vK , wobei die Größen mG = 4kg, l =
1.62m, mK = 0.055kg und y = 6.5cm vorgegeben sind. Hier beschreibt y die maximale Auslenkung
des Klotzes in horizontaler Richtung.
Aufgabe 14: Kräfte eines Massenpunktes auf einer Ellipse
Wir betrachten einen Massenpunkt mit konstanter Masse, der sich auf der Ellipse ~r = a cos(ωt)ê1 +
b sin(ωt)ê2 bewegt (s. Skizze).
a) Berechnen Sie die Kraft, die auf den Massenpunkt wirkt. Handelt es sich hierbei um eine
anziehende oder abstoßende Kraft?
b) Zeigen Sie, dass das Kraftfeld konservativ ist.
c) Berechnen Sie das Potential eines Punktes P bezüglich des Potentialnullpunks A.
d) Berechnen Sie die kinetische Energie und daraus die Gesamtenergie des Teilchens.
Aufgabe 15: Reibung
Ein Massenpunkt unterliege der Reibungskraft F~r = −mγ~v und der äußeren Kraft F~ (t) =
f.(cos(ωt)êx + sin(ωt)êy ) mit t ≥ 0.
a) Berechnen Sie daraus ~v (t) und ~r(t) mit ~v (0) = ~v0 und ~r(0) = ~0. Hinweis: führen Sie die
komplexen Vektoren ê± = êx ± iêy ein um die Integrale zu lösen.
b) Für ω 6= 0 bestimmen
Mittelwerte der absorbierten Leistung hW i = hvF i
D E SieDdie zeitlichen
E
~
~
und des Drehmoments M = ~r × F für nichtresonante Absorption γt 1.
Aufgabe 16: Raketengleichung
Man betrachte die eindimensionale, kräftefreie Bewegung einer Rakete mit konstantem Massenausstoß µ und konstanter Ausströmgeschwindigkeit c der Gase. Es sei m(t0 ) = m0 und v0 = 0.
ṁ
Die Bewegung einer solchen Rakete wird durch die Bewegungsgleichung v̇ = −c beschrieben.
m
a) Berechnen Sie aus der Bewegungsgleichung die Geschwindigkeit der Rakete in Abhängigkeit
von der Zeit.
b) Wann wird die kinetische Energie der Rakete maximal und wie groß sind ihre Masse und
Geschwindigkeit zu diesem Zeitpunkt?
c) Für den Fall, dass ein quadratisches Widerstandsgesetz (R = −αv 2 ) wirksam ist, berechne
man v(t) und untersuche den Grenzfall t → ∞.