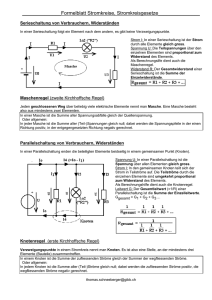
Inhaltsverzeichnis

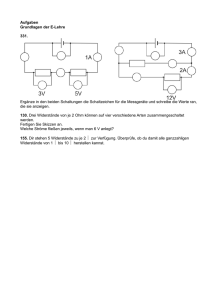
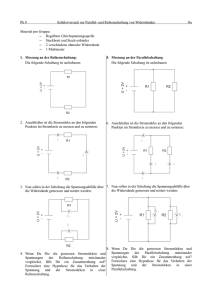
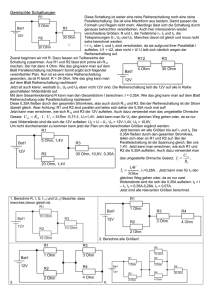
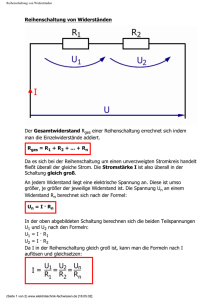
Inhaltsverzeichnis
3 Gleichstromtechnik
3.1 Grundstromkreis . . . . . . . . . . . . . . . . . . . .
3.1.1 Übersicht . . . . . . . . . . . . . . . . . . . .
3.1.2 Das Zählpfeilsystem . . . . . . . . . . . . . .
3.1.3 Grenzfall Leerlauffall . . . . . . . . . . . . . .
3.1.4 Grenzfall Kurzschlußfall . . . . . . . . . . . .
3.1.5 Ersatzschaltung für lineare Quellen . . . . . .
3.2 Kirchhoff ’sche Gesetze . . . . . . . . . . . . . . . . .
3.2.1 Erstes Kirchhoff ’sches Gesetz, Knotenregel . .
3.2.2 Parallelschaltung von Widerständen . . . . . .
Die Stromteilerregel . . . . . . . . . . . . . . .
3.2.3 Zweites Kirchhoff ’sches Gesetz, Maschenregel
3.2.4 Reihenschaltung von Widerständen . . . . . .
Die Spannungsteilerregel . . . . . . . . . . . .
3.2.5 Reihenschaltung von Spannungsquellen . . . .
3.2.6 Beispiel zum Maschenumlauf . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
26
26
26
26
27
28
28
30
30
30
33
34
34
36
37
37
Abbildungsverzeichnis
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
3.11
3.12
3.13
Eine reale Spannungsquelle besteht aus einer idealen Spannungsquelle und einem Innenwiderstand . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Der Leerlauffall . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Der Kurzschlußfall . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lineare Ersatzspannungsquelle . . . . . . . . . . . . . . . . . . . . . . . . . .
Lineare Ersatzstromquelle . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Knotenregel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Parallelschaltung von Widerständen mit Ersatzschaltbild . . . . . . . . . . . . . .
Parallelschaltung von zwei Widerständen . . . . . . . . . . . . . . . . . . . . .
Eine Parallelschaltung aus drei Widerständen R1 = 10kΩ, R2 = 5kΩ und R3 = 1kΩ .
Maschenregel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Reihenschaltung von Widerständen mit Ersatzschaltbild . . . . . . . . . . . . . .
Reihenschaltung von Spannungsquellen . . . . . . . . . . . . . . . . . . . . . .
Beispielschaltung zum Maschenumlauf . . . . . . . . . . . . . . . . . . . . . . .
25
.
.
.
.
.
.
.
.
.
.
.
.
.
27
27
28
29
29
30
31
33
34
35
36
37
38
Kapitel 3
Gleichstromtechnik
3.1
3.1.1
Grundstromkreis
Übersicht
Für den Grundstromkreis gelten folgende Eigenschaften:
• Hintereinanderschaltung von Bauelementen
• Alle Komponenten werden als idealisiert angenommen (unabhängig ihrer physikalischen Form)
• Symbole der Bauelemente symbolisieren dabei die wesentlichen elektrischen Eigenschaften des elektrischen Bauteils
• Sollen mehrere verschiedene Eigenschaften abgebildet werden, werden die entsprechenden Symbole hintereinander geschaltet, um reale Bauteile darstellen zu können
Beispiel Grundstromkreis:
Eine reale Spannungsquelle besteht aus einer Reihenschaltung einer idealen Spannungsquelle und einem (Innen-)widerstand (Abbildung 3.1).
3.1.2
Das Zählpfeilsystem
Eine Spannung wird positiv gerechnet, wenn die Zählpfeilorientierung von Pluspol zum
Minuspol gewählt wurde. Der Strom einer Stromquelle wird im allgemeinen immer vom
Pluspol über einen Verbraucher zum Minuspol fließen. Die Zählpfeile für Strom und Spannung sind bei der Quelle entgegengesetzt orientiert. An einem ohm’schen Widerstand sind
Strom und Spannung über das Ohm’sche Gesetz verknüpft, d.h. am Verbraucher müssen
die Zählpfeile für Strom und Spannung gleichgerichtet sein.
26
18.4.2006
3.1. GRUNDSTROMKREIS
Abbildung 3.1: Eine reale Spannungsquelle besteht aus einer idealen Spannungsquelle und einem Innenwiderstand
3.1.3
Grenzfall Leerlauffall
Im Leerlauffall ist der Strom I gleich Null. Dies ist genau dann der Fall, wenn der Lastwiderstand im Grundstromkreis unendlich (∞) groß ist. In der Praxis bedeutet dies, daß
der Stromkreis nicht geschlossen ist (siehe Abbildung 3.2). Die Ausgangsspannung ist
dann gleich der Quellenspannung Uq und wird im allgemeinen als Leerlaufspannung UL
bezeichnet. Die gesamte abgegebene Leistung ist ebenfalls Null.
Abbildung 3.2: Der Leerlauffall
27
18.4.2006
3.1.4
3.1. GRUNDSTROMKREIS
Grenzfall Kurzschlußfall
Im Kurzschlußfall ist die Ausgangsspannung U gleich Null. Dies tritt auf, wenn der Lastwiderstand den Wert Null hat. Der Laststrom ergibt sich zu I = URqi . Dieser Strom wird
auch als Kurzschlußstrom IK bezeichnet. Die gesamte abgegebene Leistung ist ebenfalls
Null. Der Kurzschlußfall ist in Abbildung 3.3 dargestellt.
Abbildung 3.3: Der Kurzschlußfall
3.1.5
Ersatzschaltung für lineare Quellen
Das Spannungs- und Stromverhalten von Quellen kann linear beschrieben werden (z.B.
Batterien). Aus der Leerlaufspannung Uq und dem Kurzschlußstrom Ik der Quelle läßt
sich der Innenwiderstand Ri ermitteln. Damit kann man die Ersatzschaltung als Spannungsquelle oder Stromquelle angeben. Vergl. hierzu Abbildungen 3.4 und 3.5.
Die Klemmenspannung bei der Ersatzspannungsquelle erhält man mit
Uq = U0 − Ri · I
(3.1)
Den Klemmenstrom bei der Ersatzsstromquelle erhält man mit
1
·U
(3.2)
Ri
Die beiden Schaltung sind nach außen hin völlig gleichwertig. Jedoch sollte man sich je
nach Aufgabenstellung besser für die Ersatzspannungsquelle oder für die Ersatzstromquelle entscheiden. Zu erwähnen ist noch, daß die Gleichungen für die Spannung U und
den Kurzschlußstrom Ik aus Maschenumläufen bzw. der Knotenregel entstehen. Hierzu
mehr im folgenden Kapitel.
I = IK −
28
18.4.2006
3.1. GRUNDSTROMKREIS
3.4.a Lineare Ersatzspannungsquelle
3.4.b
Abbildung 3.4: Eine lineare Ersatzquelle im Kurzschlußfall und Leerlauffall; der Kurzschlußstrom ist
Ik =
Uq
Ri
−
Uq
Ri . Die
1
Ri U
Leerlaufspannung U = Uq . Gnerell bestimmt sich der Strom I nach der Gleichung I =
3.5.a Lineare Ersatzstromquelle
3.5.b
Abbildung 3.5: Eine lineare Ersatzquelle im Kurzschlußfall und Leerlauffall; die Leerlaufspannung ist
U = Ri · Ik
29
18.4.2006
3.2
3.2. KIRCHHOFF’SCHE GESETZE
Kirchhoff ’sche Gesetze
Diese Gesetze bilden eine Säule der Elektrotechnik. Weblink:
http://de.wikipedia.org/wiki/Gustav Robert Kirchhoff
3.2.1
Erstes Kirchhoff ’sches Gesetz, Knotenregel
Der Kirchhoffsche Knotenpunksatz entspringt der Erkenntnis, daß für die Erscheinung
elektrischer Strom die sogenannte Kontinuitätsbedingung erfüllt sein muß. Daraus
leitet sich direkt die Knotenpunktregel her:
In einem Knotenpunkt ist die Summe der
zufließenden Stromstärken gleich der Summe
der abfließenden Stromstärken
Das bedeutet anschaulich, daß in einem Knoten weder Strom verloren geht, noch Strom
dazu gewonnen wird (bzw. ein Knoten kann eine elektrische Ladung speichern). Mathematisch ausgedrückt:
ΣIzu = ΣIab
3.6.a
(3.3)
3.6.b
Abbildung 3.6: Die Knotenregel: 3.6.a: Die Summe aller Ströme in einem Knoten ist gleich Null (I1 +
I2 + I3 + . . . + In = 0); 3.6.b: Wichtig: Vorzeichen beachten! (I1 = I2 + I3 + . . . + In )
3.2.2
Parallelschaltung von Widerständen
Widerstände können parallel geschaltet werden. In Abbildung 3.7 ist eine Anzahl Widerstände parallel geschaltet.
30
18.4.2006
3.2. KIRCHHOFF’SCHE GESETZE
Abbildung 3.7: Parallelschaltung von Widerständen mit Ersatzschaltbild
Aus allen Widerständen R1 . . . Rn kann ein gemeinsamer Ersatzwiderstand Rg gebildet
werden. Die Basis für die Herleitung ist die Knotenregel:
Ig = I1 + I2 + . . . + In
(3.4)
Für jeden Teilzweig i der Schaltung gilt das Ohm’sche Gesetz:
U
Ri
Ii =
(3.5)
Somit ergibt sich durch Einsetzen:
U
U
U
Ig =
+
+ ... +
=
R1 R2
Rn
1
1
1
+
+ ... +
R1 R2
Rn
·U
(3.6)
In der Ersatzschaltung ist
Ig =
U
Rg
(3.7)
also muss gelten:
1
1
1
1
=
+
+ ... +
Ersatzwiderstand
R1 R2
Rn
31
(3.8)
18.4.2006
3.2. KIRCHHOFF’SCHE GESETZE
Der Kehrwert des Ersatzwiderstandes Rg der Parallelschaltung ist gleich der Summe der Kehrwerte der Einzelwiderstände Ri
oder
der Ersatzleitwert Gg ist gleich der Summe der Einzelleitwerte Gi .
Der Ersatzleitwert ist also:
Gg = G1 + G2 + . . . + Gn
(3.9)
Die Rechnung mit Leitwerten ist immer dann zweckmäßig, wenn es sich um eine Parallelschaltung von Widerständen handelt. Es folgen noch einige Hinweise und Tricks:
Hinweis: Der Ersatzwiderstand ist immer kleiner als der kleinste Einzelwiderstand einer
Parallelschaltung von Widerständen, bzw. der Ersatzleitwert ist immer größer als der
größte Einzelleitwert bei einer Parallelschaltung von Widerständen.
Hinweis: Für den Sonderfall von n gleichen Einzelwiderständen Re in einer Parallelschaltung kann der Ersatzwiderstand mit Rg = Rne ermittelt werden bzw. ist dann der
Gesamtleitwert Gg = n · Ge .
Eine andere Form für die Berechnung von parallen Widerständen sei noch erwähnt. Für
den Fall, daß es sich nur um zwei Widerstände handelt, siehe Abbildung 3.8, gilt:
R1 · R2
R1 + R2
oder mit den entsprechenden Leitwerten ausgedrückt:
Rg =
(3.10)
Gg = G1 + G2
(3.11)
U = R1 · I1 = R2 · I2
(3.12)
Ferner gilt:
also gilt auch:
I1
R2
G1
=
=
(3.13)
I2
R1
G2
Gleichung 3.10 kann auch für 3 oder mehr parallele Widerstände hergeleitet werden.
32
18.4.2006
3.2. KIRCHHOFF’SCHE GESETZE
Abbildung 3.8: Parallelschaltung von zwei Widerständen
Die Stromteilerregel
In einer Parallelschaltung verhalten sich
die Ströme umgekehrt wie die
Widerstände; bzw. gleich wie die Leitwerte.
Rb
Ia
=R
Ib
a
Ein Beispiel hierzu:
Das Verhältnis der drei Teilströme in Abbildung 3.9 ist:
1 1 1
1
2 10
: : =
:
:
= 1 : 2 : 10
10 5 1
10 10 10
also folgt, da es 13 gleich große Anteile gibt:
I1 : I2 : I3 =
(3.14)
I1 : Ig = 1 : 13
(3.15)
I2 : Ig = 2 : 13
(3.16)
I3 : Ig = 10 : 13
(3.17)
33
18.4.2006
3.2. KIRCHHOFF’SCHE GESETZE
Abbildung 3.9: Eine Parallelschaltung aus drei Widerständen R1 = 10kΩ, R2 = 5kΩ und R3 = 1kΩ
3.2.3
Zweites Kirchhoff ’sches Gesetz, Maschenregel
Der geschlossene Stromkreis wird als Masche bezeichnet. Wenn ein willkürlicher Richtungssinn in einer Masche festgelegt wird, dann ist die Summe aller in der Masche vorhandenen Spannungen gleich Null.
Das zweite Kirchhoff’sche Gesetz, bzw. die Maschenregel lautet:
Die Summe aller Teilspannungen in einer
geschlossenen Masche ist gleich Null
oder
Die Summe aller Quellspannungen ist gleich
der Summe aller Spannungsabfälle in der
Masche
Mathematisch ausgedrückt:
Σi U = 0
3.2.4
(3.18)
Reihenschaltung von Widerständen
Widerstände können in Reihe geschaltet werden. In Abbildung 3.11 ist eine Anzahl Widerstände in Reihe geschaltet.
Die Bezugsgröße ist der Strom I, der in allen Widerständen gleich groß ist (Knotenpunktsregel) und jeweils einen Spannungsabfall Ui verursacht, also
34
18.4.2006
3.2. KIRCHHOFF’SCHE GESETZE
3.10.a Beispiel 1
3.10.b Beispiel 2
Abbildung 3.10: Die Maschenregel: 3.10.a: Die Summe aller Teilspannungen in einer geschlossenen
Masche ist gleich Null (U1 + U2 + U3 + . . . + Un = 0); 3.10.b: Wichtig: Vorzeichen beachten! ⇒ U =
U1 + U2 + U3 + . . . + Un
U1 = R1 · I
(3.19)
U2 = R2 · I
(3.20)
Un = Rn · I
(3.21)
Die Summe aller Teilspannungen (U1 bis Un ) ist gleich der Gesamtspannung Ug (Maschenregel). Man erhält durch Einsetzen:
Ug = U1 + U2 + . . . + Un
(3.22)
Damit lässt sich der Ersatzwiderstand Rg einer Reihenschaltung berechnen:
Ug = I · R1 + I · R2 + . . . + I · Rn = I · Rg
k
:I
(3.23)
also ist
Rg = R1 + R2 + . . . + Rn
(3.24)
In der Reihenschaltung ist der Gesamtwiderstand Rg gleich der Summe der Einzelwiderstände Ri .
Hinweis: Für n gleichgroße Widerstände Re gilt, daß der Gesamtwiderstand Rg = n·Re
ist.
35
18.4.2006
3.2. KIRCHHOFF’SCHE GESETZE
Abbildung 3.11: Reihenschaltung von Widerständen mit Ersatzschaltbild
Die Spannungsteilerregel
Wegen Ui = Ri · I ist der Spannungsabfall proportional dem Widerstand. Die Spannungsteilerregel lautet somit:
In der Reihenschaltung verhalten sich die
Spannungsabfälle wie die entsprechenden
Widerstandswerte:
U1
1
=R
U2
R2
oder
Ui
= RRgi
Ug
wobei Ug die Gesamtspannung und Rg der Gesamtwiderstand ist.
Ein Beispiel zur Spannungsteilerregel:
Drei Widerstände R1 = 10kΩ, R2 = 5kΩ und R3 = 1kΩ sind in Reihe geschaltet. So
ergebit sich ein Spannungsverhältnis von R1 : R2 : R3 = 10 : 5 : 1 = U1 : U2 : U3 . Die 16
Spannungsanteile ergeben nun für U1 = 10V , für U2 = 5V und für U3 = 1V .
36
18.4.2006
3.2.5
3.2. KIRCHHOFF’SCHE GESETZE
Reihenschaltung von Spannungsquellen
Eine Reihenschaltung von Spannungsquellen (Abbildung 3.12) verhält sich analog zu einer Reihenschaltung von Widerständen. So erhält man die Gesamtspannung einer Reihenschaltung von Spannungsquellen indem man die Teilspannungsn addiert Ug = Σni=1 Ui .
Abbildung 3.12: Reihenschaltung von Spannungsquellen
3.2.6
Beispiel zum Maschenumlauf
Gegeben sei die Schaltung in Abbildung 3.13:
Hierbei gelten folgende Punkte:
1. Masche III kann aus Addition von Masche I und Masche II gebildet werden (=
b
linearkombination von Maschen) ⇒ Masche III ist linear abhängig von Masche I
und Masche II
2. Masche I und Masche II sind linear unabhängig
3. Für jede Masche gilt: Σni=1 Ui = 0
37
18.4.2006
3.2. KIRCHHOFF’SCHE GESETZE
Abbildung 3.13: Beispielschaltung zum Maschenumlauf
38