Lösungen - BBZ Biel

BMS Mathematik – T2
Abschlussprüfung_11
Seite: 1/7
Lösungen
Klasse:
Name:
Aufgabe 1:
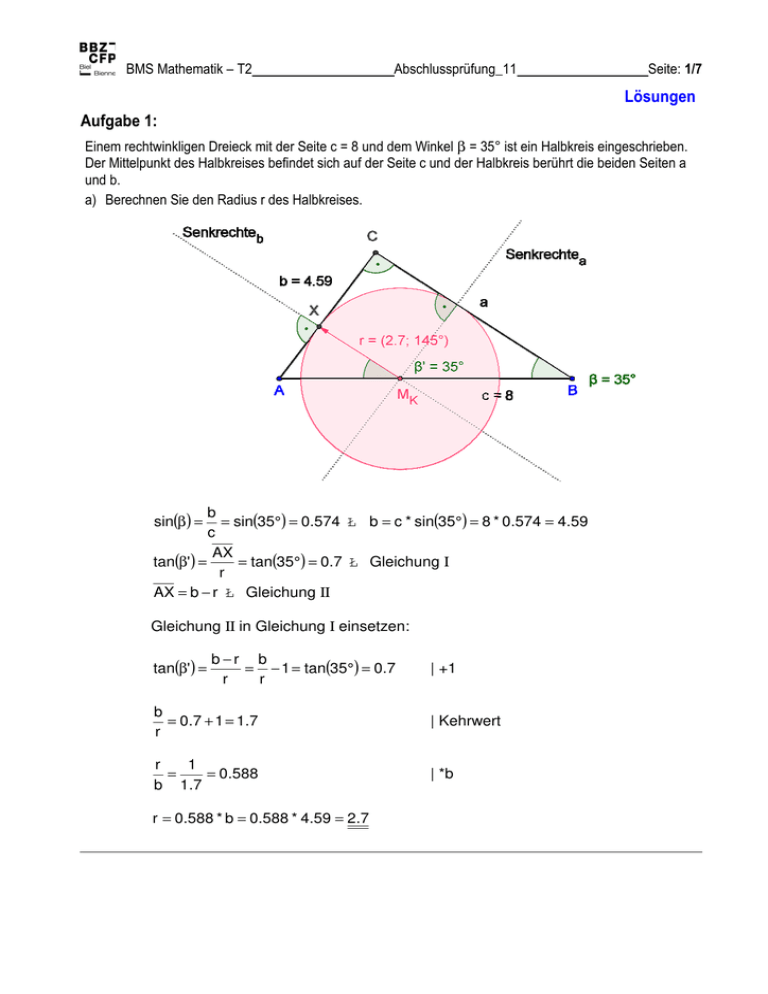
Einem rechtwinkligen Dreieck mit der Seite c = 8 und dem Winkel β = 35° ist ein Halbkreis eingeschrieben.
Der Mittelpunkt des Halbkreises befindet sich auf der Seite c und der Halbkreis berührt die beiden Seiten a
und b.
a) Berechnen Sie den Radius r des Halbkreises.
b
= sin(35°) = 0.574 Ł b = c * sin(35°) = 8 * 0.574 = 4.59
c
AX
tan(β') =
= tan(35°) = 0.7 Ł Gleichung Ι
r
AX = b − r Ł Gleichung ΙΙ
sin(β) =
Gleichung ΙΙ in Gleichung Ι einsetzen:
tan(β') =
b−r b
= − 1 = tan(35°) = 0.7
r
r
| +1
b
= 0 .7 + 1 = 1 .7
r
| Kehrwert
r
1
=
= 0.588
b 1 .7
| *b
r = 0.588 * b = 0.588 * 4.59 = 2.7
BBZ MathFachGr
MathPrue11_T2_Loesung.doc
BMS Mathematik – T2
Abschlussprüfung_11
Seite: 2/7
Lösungen
Klasse:
Name:
Aufgabe 1:
b) Gegeben ist die Funktion: f ( x ) = 3 * sin 2x + π  + 1
4

Bestimmen Sie den Wertebereich der gegebenen Funktion f(x).
W = {y − 2 ≤ y ≤ 4}
Bestimmen Sie die Periode.
T=π
Berechnen Sie die Phasenverschiebung.
t=ϕ=
π
8
c) Berechnen Sie die Lösungen der Gleichung im Intervall zwischen 0° bis 360° algebraisch.
Der Lösungsweg muss ersichtlich sein.:
2 cos 2 ( x ) − cos( x ) −
1.5P
3
=0
4
 − 3
1± 1− 4⋅ 2⋅

 4  1± 7
cos( x1; 2 ) =
=
4
4
cos( x1 ) = 0.911
Ł
x11 = 24.3 ° und x12 = 335.7 °
cos( x2 ) = −0.411
Ł
x21 = 114.3 ° und x22 = 245.7 °
BBZ MathFachGr
MathPrue11_T2_Loesung.doc
BMS Mathematik – T2
Abschlussprüfung_11
Seite: 3/7
Lösungen
Klasse:
Name:
Aufgabe 2:
a) Bestimmen Sie die Funktionsgleichung g(x) der Geraden g mit Steigung 0.5, die durch den Punkt (3/3) geht.
Berechnen Sie die Nullstelle der Geraden.
g(x)=0.5x+1.5
N(-3/0)
1P
2
b) Bestimmen Sie den Scheitelpunkt der Parabel f(x) gegeben durch f (x) = −0.5(x −1) + 5
Zeichnen Sie die Parabel ins Koordinatensystem.
f (x) = −0.5(x −1) 2 + 5 S(1/5)
1P
c) Berechnen Sie die Schnittpunkte der Geraden g(x) mit der Parabel f(x) algebraisch (mit Lösungsweg).
P1(-2/0.5)
P2(3/3)
d) Bestimmen Sie die Funktionsgleichung einer Geraden h(x), welche parallel zu g(x) liegt und
eine Tangente an die Parabel bildet.
h ( x ) = 0 .5 x + q
h( x) = 0.5 x + 4.625
BBZ MathFachGr
h(x) ∩ f (x) nur eine Lösung
1.5P
Diskriminante=0
2.5P
MathPrue11_T2_Loesung.doc
BMS Mathematik – T2
Abschlussprüfung_11
Seite: 4/7
Lösungen
Klasse:
Name:
Aufgabe 3 a:
a) Ein Fahrradhändler ergattert aus einer Versteigerung eine bestimmte Anzahl gleicher Fahrräder, wofür er
39'306.90 SFr bezahlt.
Er verkauft die Räder dann für einen Preis von 399 SFr weiter. Den Reingewinn, den er damit erzielt,
entspricht dem Betrag, den er ursprünglich für 50 Fahrräder bezahlt hat.
Wie viele Fahrräder hat der Händler erstanden?
3P
Aufgabe 3 b und c:
b) Eine Firma erhält einen Grossauftrag zum Bedrucken von Zifferblätter. Dafür werden 3 Arbeiterinnen mit
gleichem Arbeitstempo eingesetzt, welche den Auftrag in 5 Monaten erledigen würden.
Wie viele Stunden hätte eine Arbeiterin alleine an diesem Auftrag?
1P
(1 Monat hat 20 Arbeitstage zu 8 Stunden).
c) Nach einem Monat werden zusätzlich zwei neue Hilfskräfte eingesetzt, welche aber 40% langsamer
arbeiten.
Nach wie vielen Tagen kann das letzte Zifferblatt geliefert werden? (Aufgerundet auf einen Tag)
2P
a) Anzahl Fahrräder = x
Gesamtumsatz: x SFr. 399
39'306.9
Preis Ankauf:
x
Ankauf: SFr. 39306.9
Gesamtumsatz = Ankauf + Gewinn
50 ⋅ 39306.9
399 ⋅ x = 39306.9 +
x
x1 = −36.48
false
Gewinn: 50 ⋅
39 '306 . 9
x
(1)
→
399 ⋅ x 2 − 39306.9 ⋅ x − 50 ⋅ 39306.9 = 0
x 2 = 135
(1)
(1)
Der Händler hat 135 Fahrräder erstanden.
3
5⋅  = 1
→
5 ⋅ 20 ⋅ 8 ⋅ 3 = x
 x
Eine Arbeiterin benötigt alleine 2400 h.
c) Die langsameren somit 2400:0.6 = 4000 h.
Ein Fünftel der Arbeit ist bereits erledigt, somit:
b)
2  4
 3
+
tx 
=
 2400 4000  5
→
tx =
x = 2400h
(1)
4
5
2 
 3
+


 2400 4000 
t x = 457.14h
457.14
= 57.14Tage
(2)
t x = 58 Tage
8
Auf einen Tag aufgerundet: 58 Tagen nach Einstellungen der Hilfskräfte oder 78 Tage nach dem Produktionsstart.
tx =
BBZ MathFachGr
MathPrue11_T2_Loesung.doc
BMS Mathematik – T2
Abschlussprüfung_11
Seite: 5/7
Lösungen
Klasse:
Name:
Aufgabe 4:
Nach dem Unfall im Kernkraftwerk Tschernobyl im Jahre 1986 entwichen radioaktive Nuklide wie
Jod (J) 131 und Cäsium (CS) 137 in die Atmosphäre.
Jod 131 hat eine Halbwertszeit von TJ = 8 Tagen und Cäsium 137 eine von TCS = 30 Jahren.
Die Stoffe zerfallen im Verlaufe der Zeit und ihre Masse m nimmt exponentiell in Funktion der Zeit t nach
folgendem Gesetz ab: m = m0 ⋅ e − λ ⋅t
m0: ursprüngliche Masse; λ: Zerfallskonstante
a) Berechnen Sie die Zerfallskonstante λ in Abhängigkeit der Halbwertszeit T (allgemein).
m0
= m 0 ⋅ e − λT
↔
0 .5 = e − λ T
↔
ln (0.5) = −λT
2
− ln(0.5) ln (2)
ln(0.5)
λ=
=
= −λ
T
T
T
1.5P
b) Am Unfalltag werden von Jod 131 und Cäsium 137 Proben von je einem Gramm genommen,
m0 =1gr. Berechnen Sie die Masse m jeder Probe einmal nach t = 8 Tagen und einmal nach
t = 15 Jahren.
m = 1⋅ e
−
ln ( 2 )⋅t
T
t = 8 d:
t = 8 d:
mI = e
−
mCs = e
ln ( 2 )⋅8
8
−
= 0.5 g
t = 15 a: m I = e
−
ln ( 2 )⋅ 8 365
30
≈ 1g
t = 15 a: mCs = e
ln ( 2 )⋅15⋅365
8
−
ln ( 2 )⋅15
30
≈ 0 gr
≈ 0.707 g
c) Nach wie vielen Jahren hat das radioaktive Cäsium 137 noch eine Masse von m = 0.01gr?
0.01 = 1 ⋅ e
t=
−
ln ( 2 )⋅t
30
↔
−
− 30 ⋅ ln(0.01) 30 ⋅ ln(100 )
=
ln(2)
ln(2)
BBZ MathFachGr
2.5P
2P
ln(2 ) ⋅ t
= ln(0.01)
30
t = 199.32 a
MathPrue11_T2_Loesung.doc
BMS Mathematik – T2
Abschlussprüfung_11
Seite: 6/7
Lösungen
Klasse:
Name:
Aufgabe 5:
Gegeben sind die Koordinaten von vier Punkten im Raum: A = (a - 2; 0; -1); B = (a - 2; a; -1); C = (-2; a; -1)
und D = (a/2 - 2; a/2; a-1). Berechnen Sie die gesuchten Grössen in Abhängigkeit des Parameters a.
a) Berechnen Sie die Komponenten des Vektors AB .
1P
s = AB
 a − 2 − (a − 2)  0 

  
AB = 
a−0
 = a
 − 1 − (− 1)   0 

  
→
0
 
AB =  a 
0
 
b) Berechnen Sie die Länge x des Vektors AD .
x = AD
 −a
a

 − 2 − (a − 2) 
  2 
2
a
= a 
AD = 
−0
  2 

2
 a − 1 − (− 1)   a 
 


 


→
2
1.5P
2
 a a
x = −  +   + a2 =
 2 2
2
2
a
a
+
+ a2
4
4
3
x=
2
a
c) Berechnen Sie den Winkel zwischen den Vektoren AB und AD .
1.5P
a2
+0
0+
AD o AB
a2
2
1
2
=
=
⋅
=
cos(α ) =
2
2
3
3⋅a
6
AD ⋅ AB
⋅a⋅a
2
α = 65.91°
d) Berechnen Sie den Abstand (die kürzeste Entfernung) z des Punktes D zur Geraden
durch die Punkte A und C.
z = AD ⋅ sin (β ) = x ⋅ sin (β )
 − 2 − (a − 2)  − a 

  
AC = 
a−0  = a 
 − 1 − (− 1)   0 

  



β = a cos


z=
BBZ MathFachGr
3
2

 AD o AC
β = a cos
 AD ⋅ AC

2P





AC = a 2 + a 2 + 0 = 2a

a2 a2
+
+0 
 a2 
 1 

2
2
 = a cos
 = 54.56°
= a cos

2 
3
3
3a 


⋅ a ⋅ 2 ⋅ a 
2

⋅ a ⋅ sin (54.56) = a
z=a
MathPrue11_T2_Loesung.doc
BMS Mathematik – T2
Abschlussprüfung_11
Name:
Seite: 7/7
Lösungen
Klasse:
Aufgabe 6:
Gegeben ist eine gerade quadratische Pyramide ABCDS ( Spitze bei S)
mit der Grundfläche ABCD = 50cm 2 und der Höhe h = 12cm.
a) Erstellen Sie eine korrekt beschriftete Skizze.
1P
b) Der Punkt P liegt auf der Kante CS , wobei gilt: CP = 3cm .
Berechnen Sie den Abstand des Punktes P zur Spitze S.
[ ]
AC = ( 50 ) + ( 50 )
AB = BC = 50
2
2
0.5p
= 100 = 10cm
M = Mittelpunkt der Diagonalen AC
CM = 5cm
2
0.5p
2
CM + MS = CS
2
0,5P
5 2 + 12 2 = 169
CS = 13
PS = CS − CP
PS = 13cm − 3cm = 10cm
0,5P
c) Berechnen Sie den Winkel ∠ACS .
MS 12
=
γ = 67,3801°
1P
5
CM
d) Berechnen Sie den Winkel ε = ∠CMP , wobei M der Diagonalenschnittpunkt der Grundfläche ist.
tan γ =
Kosinussatz:
2
2
MP = MC + CP − 2 ⋅ MC ⋅ CP ⋅ cos γ
0,5P
MP = 5 2 + 32 − 2 ⋅ 5 ⋅ 3 ⋅ cos 67,3801° = 4,73936cm
0,5P
Sinussatz:
sin ε sin γ
=
CP
MP
3 ⋅ sin 67,3801°
sin ε =
4,73936
ε = 35,7539°
BBZ MathFachGr
0,5P
0,5P
MathPrue11_T2_Loesung.doc