Inhaltsverzeichnis 1 Grundlagen E-Lehre und Energie

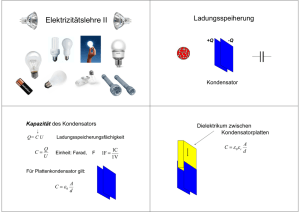
Herr Amrein: ·Physik J11· 2Std
Inhaltsverzeichnis
1Grundlagen E-Lehre und Energie-Lehre.............................................................................1
1.1Ladung und Stromkreis.................................................................................................1
1.2Reihenschaltung...........................................................................................................2
1.3Parallelschaltung..........................................................................................................3
1.4Energie und Leistung....................................................................................................4
1.5Leistung im Stromkreis.................................................................................................5
1.6Energie, Spannung und Ladung...................................................................................5
1.7Elektrisches Potential...................................................................................................5
2Teilchen in Feldern...............................................................................................................5
2.1Das Elektrische Feld.....................................................................................................5
2.2Influenz, Polarisation und der Faradaysche Käfig........................................................6
2.3Die stärke des elektrischen Feldes...............................................................................8
2.4Spannung und Energie im Plattenkondensator..........................................................10
2.5Teilchenbewegung im E-Feld.....................................................................................12
2.6Kapazität eines Kondensators....................................................................................14
2.7Energie eines Kondensators / eines elektrischen Feldes..........................................16
2.8Auf- und Entlade-Vorgang am Kondensator...............................................................17
3Magnetismus und Teilchen................................................................................................19
3.1Magnete und Magnetfelder.........................................................................................19
3.2Strom erzeugt Magnetismus.......................................................................................20
3.3Magnetismus verändert den Strom............................................................................22
OHP:
Der erste Tag
Vorlesen:
Regeln und Organisation (auch eine Übung zu k,m,M,G)
1 Grundlagen E-Lehre und Energie-Lehre
1.1 Ladung und Stromkreis
Tafel:
▪
Grundlage für jeden Stromkreis sind frei bewegliche Ladungen (Elektronen)
▪
In Holz sind alle Elektronen fest. Sie halten die Atome zusammen.
▪
Auch Eisen in werden die Atome von Elektronen zusammengehalten.
Zusätzlich gibt es jedoch noch frei bewegliche Elektronen. Diese können
Strömen.
▪
Wir reden später immer von diesen freien Elektronen
Animation:
C
C
C
C
Fe
Fe
Fe
Fe
C
C
C
C
Fe
Fe
Fe
Fe
Stromkreis Baukasten (Datei „Stromkreise vergleichen“ laden )
Problem:
In welchem Stromkreis ist die Stromstärke I größer?
Idee1:
Wir zählen die Ladungsteilchen die in einer bestimmten Zeit t „um die Ecke
fließen“.
→ Stromstärke ist Ladung pro Zeit →
I=
Q
t
Idee2:
Ladung wird von Spannung angetrieben und von Widerstand gebremst. Im
zweiten Stromkreis ist die Spannung zwar etwas größer aber die Widerstand
viel größer als im ersten Stromkreis.
→ Stromstärke ergibt sich aus Verhältnis zwischen Spannung zu Widerstand
U
→ I=
R
Merke:
Für einen Stromkreis braucht es freie Elektronen (freie Ladung)
I=
Stromstärke ist Ladung pro Zeit →
Q
t
Q 2C
=0,4 A
z.B. I = =
t 5s
Stromstärke ergibt sich aus Verhältnis zwischen Spannung zu Widerstand
U
U 14 V
=0,56 A
→ I=
z.B. I = =
R
R 25 Ω
Austeilen:
Info elektrische Grundgrößen
Aufgabe:
Einfache Aufgaben zur Stromstärke
1.2 Reihenschaltung
Tafel:
U=4V
50Ω
U=6V
U=3V
50Ω
U=4V
50Ω
12V
Animation:
U=6V
Stromkreis Baukasten
12V
U=4V
50Ω
12V
U=9V
150Ω
•
Reihenschaltung mit Glühbirnen bauen
•
Zusätzlichen Widerstand hinzunehmen, Stromstärke beobachten.
Spannungen Messen.
•
Einen Widerstand vergrößern, Spannungen erneut messen.
Merke:
Sind zwei Verbraucher in Reihe (nacheinander) so teilt sich die Spannung
der Spannungsquelle auf. U ges =U 1+U 2+...
Durch jeden Verbraucher fließt jedoch der selbe Strom I ges=I 1=I 2=…
Der Gesamtwiderstand ist die Summe der Einzelwiderständen
Rges =R1+R 2+.. .
Die Spannung teilt sich in Reihenschaltungen anteilig zur
R1
⋅U
Widerstandsgröße auf: U 1=
Rges ges
Aufgaben:
Reihenschaltung
1.3 Parallelschaltung
Tafel:
I=0,4A
I=0,2A
12V
Animation:
I=0,2A
U=12V
U=12V
Stromkreis Baukasten
▪
Stromkreis bauen (Glühbirne)
▪
Zweite und dritte Birne parallel hinzunehmen. Spannungen und Ströme
messen.
▪
Widerstand einer Birne herauf- und einer herabsetzen. Erneut Spannungen
und Ströme messen
Schaltet man eine zweite Birne parallel zu einer ersten Birne, so ändert
Birne1 die Helligkeit nicht.
Im Gesamtstromkreis fließt nun allerdings doppelt so viel Strom wie zuvor.
Verbraucher
Erklärung:
Die Spannung teilt sich bei der
Parallelschaltung nicht auf. Bei Birne1 ist die
Spannung unverändert.
Die zweite parallele Birne bietet einen
zusätzlichen Weg für die Ladung von A nach
B zu kommen, somit kann im gesamten
Stromkreis mehr Ladung fließen als bei nur
einer Birne
Pumpe
Merke:
Sind zwei Verbraucher parallel (nebeneinander) so liegt an jedem
Verbraucher die Spannung der Spannungsquelle an. U ges =U 1=U 2 =...
Durch jeden Verbraucher fließt eine separate Stromstärke. Die Summe der
Einzelströme ist die Stromstärke Iges hinter der Spannungsquelle
I ges=I 1+I 2 +.. .
Der Gesamtwiderstand ist kleiner als jeder Einzelwiederstand
1
1 1
= + +.. .
R ges R 1 R 2
Bsp: R1=50Ω R2=100Ω
Aufgabe:
1
1 1
1
1
1
= + =
+
=0,03 →R ges=33,3 Ω
Ω
R ges R 1 R 2 50 Ω 100 Ω
Parallelschaltung
Diskussion:
Warum ist für den Haushalt eine Parallelschaltung sinnvoll und keine
Reihenschaltung?
1.4 Energie und Leistung
Einstieg:
Was hat das Bild mit den Begriffen „Energie“ und „Leistung“ zu tun? Erkenne
welcher Wert für beide Bilder gleich und welcher verschieden ist.
Tafel:
▪
Ob ein Gerät viel leistet, erkennt man daran, wie schnell des den vorhanden
Energie-Vorrat umwandelt.
▪
Leistung P ist also Energieumwandlung pro Zeit.
▪
Leitung ist P, Energie ist W, Zeit ist t. Welche Formel gibt den Satz oben
W
P=
P=W−t
wieder? P=W⋅t
t
Aufgaben:
(Austeilen)
1. Ein Fön wandelt die Energie W=20kJ in t=40s um. Berechne die Leistung P.
2. Ein Mixer mit P=450W läuft t=25s lang. Welche Energie W wurde
umgewandelt?
3. Fünf Liter Benzin haben die Energie W=175·106J. Ein Porsche in Vollleistung
(Bleifuß) wandelt dies in t=800s um. Berechne die Leistung P
4. Ein Trabi hat die Leitung P=15kW. Welche Zeit t lässt sich mit der Energie
von 5 Litern Benzin fahren?
Merke:
Leistung P ist Energieumsatz pro Zeit
z.B. P=
P=
W
t
W 200 J
=
=50W Einheit von Leistung W (Watt).
t
4s
Sonstiges:
Der Begriff „Kilowattstunde“ bezeichnet Energie! Nach der Formel
W =P⋅t
1kWh=1kW·1h=1000W·3600s=3.600.000J
1.5 Leistung im Stromkreis
Animation:
Stromkreis Baukasten (Laden: Parallelschaltung)
Tafel:
Die Leistung P einer Birne erkennt man an der Helligkeit!
Liegt an drei Birnen die selbe Spannung U an, so leistet die am meisten,
durch die der meiste Strom I fließt.
Animation:
Stromkreis Baukasten (Laden: Reihenschaltung)
Fließt durch drei Birnen der selbe Strom I, so leistet die am meisten, an der
die meiste Spannung U abfällt.
Ergebnis:
Sowohl Spannung U als auch Strom I ist wichtig für eine große Leitung P.
Frage:
Wie sieht eine Formel für P aus? P soll groß sein, wenn I oder U groß sind.
Merke:
Leitung P steigt mit Spannung U und Stromstärke I. P=I⋅U
z.B. P=I⋅U=0,21 A⋅12V =2,52W
Aufgaben:
Strom Spannung Leistung
PC-Raum:
Praktikum am PC
1.6 Energie, Spannung und Ladung
U=
W
Todo!
q
1.7 Elektrisches Potential
Todo
2 Teilchen in Feldern
2.1 Das Elektrische Feld
Versuch:
Bandgenerator lässt Wattekügelchen
fliegen.
Tafel:
Wir wissen das „Plus und Plus“ sich abstößt und „Plus und Minus“ sich
anziehen. Somit können wir den Weg unsere drei kleinen Probeladungen q+
vorhersagen.
q+
q+
Q+
Q-
q+
Merke:
Ladungen „spüren“ einander durch ein sog. elektrisches Feld (E-Feld).
Wir zeichnen das E-Feld durch (rote) Feldlinien.
Pfeilrichtung: Wohin bewegt sich eine positive Probeladung
Pfeildichte: Stärke des E-Felds
Aufgabe:
Arbeitsblatt
+
+
+
+
+
+
+
-
+
+
+
-
+
+
+
+
+
+
+
+
+
+
-
+
Zeichne die elektrischen Feldlinien ein. (blauen Pfeilen)
Feld eines Elektroskops. Man sieht
wie „Abstoßung“ als Feld aussieht.
Versuch:
Grießkörner in Hochspannung oder Graphitpulver in Hochspannung
Film:
Grießkörner in Hochspannung
Versuch:
Geladenes Elektroskop
Animation:
E-Feld virtuell erstellen
PC-Spiel:
Elektric Hockey
4. Std: Elektrisches Potential mit „E-Feld virtuell erstellen“ und Versuch
4. Std. g-Feld
4. Std. Coulombgesetz vs. Graviationsgesetz
2.2 Influenz, Polarisation und der Faradaysche Käfig
Versuch:
Elektroskop schlägt auf Grund von Influenz aus.
Tafel:
Das Elektroskop besteht aus Eisen. In Eisen gibt es frei bewegliche
Elektronen - . Wandert ein Elektron ab. So bleibt ein positiv geladenes
Atom zurück + . (Die Atome können übrigens nicht Wandern)
+++++
+++++
+++++
- + -+ +
- +
-
- + -+ +
- +
-
+-
+-+
-+
Bild1
+-
-+
+-
-+
Bild2:
Wie bewegen sich
die Elektronen?
Was ist die Folge?
(Gruppieung→ Aufheben)
Aufgabe:
Begründe, dass der Zeiger im Elektroskop (Bild1) bisher noch keinen
Grund hat sich vom Elektroskop abzustoßen.
Aufgabe:
Erstelle eine Zeichnung die zeigt, wie sich die freien Elektronen bewegen,
wenn man einen Stark positiv geladenen Körper darüber hält. Beschreibe
den gesamten Vorgang in 4-6 Sätzen.
Merke:
Bewegen sich freie Metall-Elektronen aufgrund eines elektrischen
Feldes, so nennt man das „Influenz“.
Versuch:
Faraday Käfig (Elektroskop im Drahtrahmen)
Erklärung:
+-
+-
+-
+-
+-
+-
++-
++- +-
+-
+-
+++++
+++++
+++++
+++++
+++++
+++++
+++++
+++++
+++++
+-
-+- - +- -- +- -- +- -- +
+-
++-
++- +-
+-
+-
+-
-+- - +- -- +- -- +- -- +
+-
++-
++- +-
+-
+-
+-
Aufgabe:
Fasse das „Prinzip Faradayscher Käfig“ mit eigenen Worten zusammen. (4-8
Sätze)
Merke:
Mit einem Faradayschen Käfig lässt sich das elektrische Feld aber auch
elektromagnetische Strahlung* abschirmen.
*schnell vorbei fliegende elektrische Felder.
Versuch:
Ballon an Wand
Versuch:
Watte des geladenen Bandgenerators wird auch von der Hand angezogen.
Video:
Polarisation und Influenz
Erklärung:
Polarisation und Influenz
Metall-Atom: Die freien Elektronen bewegen
sich im elektrischen Feld. Das nennt man
Influenz
-
+
E-Feld
Sonstige Atome: Die Elektronen können sich zwar
nicht lösen, jedoch verschiebt sich die
Elektronenhülle im elektrischen Feld. Das Atom
bekommt eine positive und eine negative Seite.
Die nennt man Polarisation.
δ-
δ+
E-Feld
Merke:
Polarisation bedeutet, dass sich die Atomhülle eines Atoms verschiebt.
Damit bekommt das Atom eine positive und eine negative Seite.
Animation:
Ballon an Wand (1.keine Ladungen 2.Ladungsunterschiede 3.alle Ladungen)
Film:
Grießkörner in Hochspannung (werden polarisiert)
2.3 Die stärke des elektrischen Feldes
Versuch:
Plattenkondensator
Bem:
*Isolation bzw. Glasplatte verwenden.
*Projektion kann Ausschlag markieren
*Kugel, Rasierklinge oder Alupapier denkbar.
*Halbierung der Ladung auf q/2 zeigt halben
Ausschlag ist nicht möglich
Platten
kondensator
q
E
*zur Wiederholung lässt sich aus der
Ausschlag ohne q nur auf Grund der Influenz
zeigen.
F
U=4000V
+
-
Messung:
mit Ladungsmesser: z.B. q=4nC=4·10-9C bei höherer Spannung q=10nC
Aufgabe:
Ergänze die Sätze:
Bei gleichem E-Feld aber doppelter Ladung q ist die Kraft F….
Bei doppeltem E-Feld aber gleicher Ladung q ist die Kraft F…
Bei doppeltem E-Feld und doppelter Ladung q ist die Kraft F…
Bei doppeltem E-Feld und halber Ladung q ist die Kraft F…
Bei gleichem E-Feld aber 10-facher Ladung q ist die Kraft F
Ergebnis:
Die Kraft F die die Ladung q im E-Feld erfährt ist proportional zu q.
Um die Feldstärke E unabhängig von q zu machen definiert man: E=
F
q
Merke:
Man definiert die elektrische Feldstärke E:
E=
F el
q
z.B. E=
F el 4 mN 4⋅10 -3 N
N
=
=
=200000
-9
q 20 nC 20⋅10 C
C
Eine Ladung q erfährt im E-Feld die elektrische Kraft F el:
z.B. F el=q⋅E=5⋅10 -9 C⋅1,23⋅107
F el=q⋅E
N
=0,0615 N
C
Wiederholung:
Die Kugel im Plattenkondensator beginnt bei hohen Spannungen auch ohne
Ladung zu pendeln. Auslöser zu beginn sind Effekte der Influenz.
Spickzettel:
m → 10-3
μ → 10-6
k → 103
M → 106
n → 10-9
p → 10-12
G → 109
Beispiel: Für 4-Stünder
(Herleitung, Rechnung todo)
Film:
Wdh Telekolleg Elektrisches Feld
Telekolleg Elektrisch Feld E=F/Q
Versuch:
Plattenkondensator
Platten
kondensator
d
U=4000V
+
-
Beobachtung1:
Dreht man die Spannung langsam hoch erkennt man: Bei höherer Spannung
bewegt sich die Kugel weiter aus der Ruhelage als bei geringer Spannung.
Ergebnis1:
Die Feldstärke im Plattenkondensator ist proportional zu Spannung:
E∼U
Beobachtung1:
Schiebt man bei konstanter Spannung die Platten zusammen erkennt man:
Bei kleinem Plattenabstand d bewegt sich die Kugel weiter aus der Ruhelage
Ergebnis2:
Die Feldstärke im Plattenkondensator ist antiproportional zum
1
Plattenabstand: E∼
d
Bemerkung:
Beobachtung1 und 2 reichen eigentlich nicht aus um so etwas präzises wie
1
E∼U und E∼ zu formulieren. Genaue Messreihen sind jedoch sehr
d
aufwendig.
Merke:
In einem Plattenkondensator kann die Feldstärke E aus Spannung U und
Plattenabstand d berechnet werden:
E=
U
d
z.B. E=
U 20000 V
V
N
=
=125000 =125000
d
0,16 m
m
C
Aufgaben:
E-Feld bestimmen
Aufgabe:
Eine Ameise (m=0,00001kg) wird, schonend für das
Tier, mit einer Ladung von q=7nC aufgeladen und soll in
einem horizontalen Plattenkondensator zum schweben
gebracht werden.
Fel
+++++
FG
a)Ergänze die Skizze mit dem Vorzeichen der
Ameisenladung (+ oder -) und zeichne (blau) die
elektrischen Feldlinien des Kondensators hinzu.
-----
b)Bestimme aus der Masse m der Ameise deren Gewichtskraft F G und
bestimme nun die nötige elektrische Feldstärke E, die die Ameise in der
Schwebe hält. (Es gilt: g=9,81 N/kg)
c)Der Plattenabstand beträgt d=8cm. Welche Spannung U muss an die
Platten angelegt werden?
Film:
Millikan-Versuch (einfache Version)
Merke:
Millikan gelang es 1910 die Ladung q=e eines einzelnen Elektrons auf ein
Öltröpfchen zu bringen. Indem er das Tröpfchen im Plattenkondensator
schweben ließ, konnte er die Elementarladung e bestimmen.
e=1,6⋅10−19 C
Aufgabe:
DB S 11/12 Seite 14 und 21 (Seite1 als PDF erzeugen. Tafel:
s
F= ⋅G )
l
2.4 Spannung und Energie im Plattenkondensator
Versuch:
Glimmlampe am Plattenkondensator
Glimmlampe
Der Kondensator wird
geladen, dann getrennt
und die Energie W rasch
mit der Glimmlampe
nachgewiesen.
Platten
kondensator
U=200V
+
-
Kondensator auf
Glasplatte stellen
Beobachtung:
Das Leuchten der Glimmlampe zeigt, dass der Kondensator (U=200V)
Energie W speichert.
Wir wissen jedoch, dass eine Batterie (U=1,5V) deutlich mehr Energie
speichern kann.
→ Es kommt nicht nur auf die Spannung an!
Gedanken-Experiment: (austeilen)
s
W =F⋅s
W=F·s
=20N·0,8m
=16Nm
=16J
F
Wir berechnen die Elektrische Energie Wel des
Kondensators so, wie wir auch mechanische Energie
W berechne:
Wir stellen uns einen bereits geladenen
Plattenkondensator vor. Hier wollen wir nun die Ladung q= -100nC auf die
andere Seite tragen. Dabei entsteht ein zurückbleibendes „Loch von
+100nC“. Insgesamt wurde die Ladung q=100nC voneinander getrennt.
W el =F⋅s
= F el⋅d
=q⋅E⋅d
+
+
d
+ q F
el
Platten
+
kondensator+100nC -100nC
Für das Elektrische Feld E gilt:
+
U
+
E=
. Dies setzen wir ein und
+
d
erhalten:
-
W el =F⋅s
= F el⋅d
=q⋅E⋅d
U
=q⋅ ⋅d =q⋅U
d
Merke:
Deutung der Formel
W el =q⋅U :
W el =q⋅U → Eine Batterie kann auch bei geringer Spannung U=1,5V viel
Energie W speichern, wenn hier viel Ladung q getrennt vorliegt.
W el
→ Der Begriff „Spannung“ sagt etwas über die Energie pro
q
Ladungs-Teilchen aus.
U=
Versuch:
Energie im Plattenkondensator vergrößern
Beobachtung:
Ein Plattenkondensator wird mit U=150V geladen und getrennt. Nun werden
die Platten um Δd weiter auseinander gezogen. Eine Glimmlampe leuchtet
nun heller.
Erklärung:
Die Energie die beim
auseinander ziehen
(entgegen der
elektrischen Kraft, nicht Platten
entgegen der Reibung) kondensator
zusätzlich dem
Kondensator zugeführt
wird, bekommt man nun
als Licht zurück
Versuch:
+
+
+
+
+
+
+
F
p-e
lam m
lim
Δd
pe
lam
m
im
Gl
G
Feste Ladungsmenge Q im Plattenkondensator
+
+
+
+
+
+
+
Q
Beobachtung:
Zieht man die Platten
auseinander, so steigt
die Spannung U.
Platten
kondensator
Erklärung:
Q
d
U
Da man die Ladung Q
weiter trennt, steigt die
Energie Wel. Damit steigt aber auch die Spannung U, die ja die Energie pro
Ladungs-Teilchen ist.
2.5 Teilchenbewegung im E-Feld
Tafel:
Viele Geräte (Röhren-Fernseher, Oszilloskop, Röntgen-Gerät,
Elektronenstrahlröhre) basieren auf folgender Idee:
→ Geladene Teilchen im E-Feld
→ Teilchen werden beschleunigt
→ Die Wandeln elektrische Energie in kinetischer Energie um
→ Teilchen prallen auf eine Scheibe
→ Die kinetische Energie wird dort zu Licht
Film:
Braunsche Röhre
Versuch:
Elektronenstrahlröhre
Anode
Schirm
GlühKathode
Elektronen treten bei der Kathode
aus. Die Elektronen sind Ladungen
die vom Pluspol (Anode) getrennt
U =6V
Ub
sind. Die Elektronen haben also
elektrische Energie Wel. Nun beschleunigen die Elektronen hin zur Anode.
und wandeln so ihre elektrische Energie Wel in kinetische Energie Wkin um:
+
-
h
Kathoden-Austritt:
100% Wel
0% Wkin
Mitte zw. Kathode und Anode:
50% Wel
50% Wkin
Anode und dahinter:
0% Wel
100% Wkin
Bem.: Die Kathode ist hierbei wirklich negativ geladen, die Anode ist geerdet, daher werden die Elektronen nicht
hinter der Anode zur Anode zurück gezogen.
Beispiel:
Geschwindigkeit der Elektronen in der Elektronenstrahlröhre
geg. Ub=2,5 kV , me=9,11·10-31kg, q=e=1,6·10-19C
ges. v
W kin=W el
1
m v 2=eU
2 e
2eU
v 2=
me
2eU
v=
me
v=
√
√ √
2eU
2⋅1,6⋅10−19⋅2500 m
m (ca. 10% Lichtgeschw.)
=
=29.600 .000
−31
me
s
s
9,11⋅10
Merke:
Deutung der Formel
W el =q⋅U :
Wel ist die Energie eines Teilchens mit der Ladung q.
Werden Teilchen aufgrund von Ladung im E-Feld beschleunigt, so gilt
Energie-Erhaltung:
W kin=W el
Wird die Spannung U voll durchlaufen und die Reibung vernachlässigt, so
2qU
hat das Teilchen eine Endgeschwindigkeit von v =
m
Aufgabe:
√
+
Wattekügelchen (m=0,00005g=...kg) werden zwischen
+ q+ q+
zwei Platten mit der Spannung U=6kV beschleunigt.
+
Die Kügelchen tragen die Ladung q=+6nC. Die Platten q+
+
stehen 70cm auseinander.
+
U
a) Berechne die Geschwindigkeit v die sie erreichen
können.
-
b) Die Kügelchen kommen nur mit der Geschwindigkeit v=7m/s an der
anderen Seite an. Welcher Anteil ihrer Energie ging durch Luftreibung
verloren?
c) Ein Wattekügelchen wird nun mit der Pinzette bei der positiven Platte
genommen, zu 1/3 zur negativen Platte geführt und nun losgelassen.
Entscheide ob es nun im Vergleich zu a) schneller/langsamer/gleich schnell
bei Q- ankommt und begründe.
d) Berechne die Kinetische Energie Wkin und Geschwindigkeit v von
Aufgabenteil c) mit der Formel: W =F⋅s
Aufgabe:
U
Xe+
Die Deep-Space-1 Raumsonde wurde 1998
Xe+ Xe+ Xe+ Xe+
mit einem Xenon-Ionen-Antrieb
Xe+
ausgestattet. Hierbei wurden Xenon-PlusIonen (m=8,96·10-26kg, q=1,6·10-19C) mit
einer Spannung von U=1200V beschleunigt. Insgesamt hatte die DeepSpace-1 Raumsonde 82kg Xenon als Treibstoff dabei.
Xe+
a)Vervollständige die Skizze in deinem Heft. Wo muss der +Pol, wo der -Pol
sein, damit die Xe+Ionen beschleunigen?
b)Bestimme die Geschwindigkeit mit der die Ionen die Düse verlassen.
c) Über ein Solar-Panel wird der Antrieb elektrisch versorgt. Wie viel Energie
W wurde aufgewandt um die 82kg „herauszuschießen“.
d) Die Leistung des Antriebs wird von der NASA mit 2500W angegeben. Wie
lange könnte der Antrieb nach unseren Energie-Berechnungen laufen?
Aufgabe:
Elektronen (me=9,11·10-31kg,
q=e=1,6·10-19C) werden in einer
Braunschen Röhre mit UA=1500V
beschleunigt.
a) Berechne die Geschwindigkeit vx
der Elektronen.
b) Hinter dem Anoden-Ringe befinden
sich zwei 10cm lange horizontale Platten. Welche Zeit t brauchen die
Elektronen um die 10cm lange Strecke in x-Richtung zu durchlaufen.
c) An den Platten liegt eine Spannung U B an, so dass die Elektronen
sy=0,02m in y-Richtung gezogen werden. Es handelt sich um eine
beschleunigte Bewegung in y-Richtung. (vy=a·t ; sy= ½ a·t² ; F=m·a). Welche
Beschleunigung a und welche Kraft F wirkt auf die Elektronen zwischen den
Platten?
d) Die Platten haben den Abstand d=8cm voneinander. Welche Spannung U B
liegt an, damit die Strecke von sy wie in c) erreicht wird?
2.6 Kapazität eines Kondensators
Versuch:
Q
Auf einen Kondensator
wird durch eine
Spannungsquelle
geladen und abgetrennt.
Anschließend wird mit
einem Ladungsmesser
die Ladungen Q des
Kondensators
gemessen.
Platten
kondensator
-
+
+
+
+
+
Q
U
+
-
Messu
ng:
U in V
0
0,5
1
1,5
2
2,5
Kondensator mit großem
Abstand d=5cm
Q in nC 0
12
22
39
49
63
Kondensator mit kleinem
Abstand d=2cm
Q in nC 0
16
36
60
78
98
Handelsüblicher 100pF
Kondensator
Q in nC 0
55
120
100
Q in nC
80
60
40
20
0
0
0
0,5
1
1,5
2
2,5
3
U in kV
Mündlich:
Die Fähigkeit eines Kondensators Ladung aufzunehmen wird als Kapazität C
des Kondensators bezeichnet.
Entscheide welcher Kondensator die größere Kapazität hat:
A nimmt bei U=20V die Ladung Q=4C auf.
B nimmt bei U=30V die Ladung Q=5C auf.
Merke:
Die Ladung (Q+ Q-) die ein Kondensator aufnimmt ist proportional zur
Spannung U. Die Kapazität C eines Kondensators berechnet sich:
Q
C=
U
Beispiel:
Q 0,1 nC
C= =
=2,5⋅10−12 F=2,5 pF
U 40 V
F:Farad
Merke:
Für einen Plattenkondensator gilt:
A
C=ϵ0⋅
d
A :Fläche einer Platte (m²) d : Plattenabstand( m ) ϵ0=8,85⋅10−12 C /(Vm)
Bem:
Ladung nur einfach und Platte nur einfach betrachten.
4Stundig:
Dieelektrika
Beispiel:
Kapazität des Versuchskondensators mit beiden Formeln
Q 98 nC
C= =
=3,92⋅10−11 F=39,2⋅10−12 F=39,2 pF
U 2500 V
Platten → d=0,26m → r=0,13m →
A=π r 2=3,14⋅0,132 m2=0,0531 m2
A
0,0531 m ²
−12 C
C=ϵ0⋅ =8,85⋅10
⋅
=23,5 pF
d
Vm 0,02 m
Aufgaben:
Kapazität des Kondensators
4Stundig:
Kondensator in Reihen- und Parallelschaltung
2.7 Energie eines Kondensators / eines elektrischen Feldes
Neu:
Die Bedeutung der Fläche in einem Diagramm
Wiederholung:
Getrennte Ladung stellt eine Form von Energie dar.
W el =Q⋅U
Gedanken-Experiment:
Wir stellen uns einen isolierten Plattenkondensator mit C=1F, an dem eine
Spannung von U=1V anliegt. Nun werden nach einander Q=1CLadungsportionen getrennt. Jedes mal wird dazu W=Q·U=1J an Energie
gebracht. Diese Energie steckt nun im Plattenkondensator
U in V
1
1
1
1
1
1
1
1
1
Q in C
1
1
1
1
1
1
1
1
1
W in J
1
1
1
1
1
1
1
1
1
U
+1C
U=1V
Q
=-1C
1,2
1
0,8
0,6
0,4
0,2
0
W=Q·U
1
1
1
1
1
1
1
1
1
Q
Dies ist aber
FALSCH, denn mit
jedem Coulomb an Ladung, stiegt die Spannung am Kondensator und somit
auch die Kraft, gegen die die Ladung getrennt werden muss. Folglich erhöht
sich nach jedem Coulomb die Energie, die für das nächste Coulomb
aufgewandt werden muss.
U in V
1
2
3
4
5
6
7
8
9
Q in C
1
1
1
1
1
1
1
1
1
W in J
1
2
3
4
5
6
7
8
9
-
10
8
U in V
+1C
+ U=5V
+
Q
+
=-1C
+
+
6
W= ½ Q·U
4
2
0
Die Fläche des Dreieckes im QU-Diagramm ist ein Maß für die
Energie dies Kondensators.
Es gilt:
1
1
1
W C = Q⋅U = (C⋅U )⋅U= C⋅U 2
2
2
2
Merke:
Für die Energie eines Kondensators gilt:
1
1
1
1
1
Q in C
1
1
1
1
1
1
2
W C = Q⋅U bzw W C = C U
2
2
4Stundig:
Energiedichte
Versuch:
Geladener 10000μF Kondensator bringt Lampe zum leuchten.
Beispiel:
Ein 10000μF Kondensator wird mit 7V geladen. Er lässt eine Birne 0,3s lang
leuchten. Welche Leistung bringt die Birne?
geg.: C=10000μF, U=7V
ges.: W
1
1
W = C U 2= ⋅10000⋅10−6 F⋅( 7 V )2=0,245 J
2
2
geg.: W=0,245J, t=0,3s
ges.: P
P=
W 0,245 J
=
=0,816 W
t
0,3 s
Aufgaben:
Energie des Kondensators
Tafel:
Kondensator vs Batterie
Pro Batterie: AA-Batterie: 12000J
10000μF-Kondensator: 8J
Pro Batterie: Nahezu gleichbleibende Spannung beim entladen
Pro Kondensator: unendlich oft aufladbar
Pro Kondensator: verlustfrei auf- entladen
Pro Kondensator: extrem schnell laden und entladen
Pro Kondensator: Spannungswerte exakt berechenbar
2.8 Auf- und Entlade-Vorgang am Kondensator
PC-Raum:
Praktikum Aufladevorgang
Animation:
Wechselstrom-Baukasten
Versuch:
Aufladen eines Kondensators
Skizze:
I
R=100Ω
R
C
U=10V
Entladen
Messung:
Zeit t/s
0
20
40
60
80
100
120
C=10000μF
R=4000Ω
Strom
I / mA
3,5
2,5
1,7
1,25
0,8
0,65
0,5
C=10000μF
R=2000Ω
Strom
I / mA
6,3
3,3
1,6
0,95
0,6
0,4
0,25
C=20000μF
R=2000Ω
Strom
I / mA
6,6
4,7
3,3
2,4
1,8
1,4
1,1
7
6
I in mA
5
4
3
2
1
0
0
20
40
60
80 100 120 140
C=10000μF
R=4000Ω
Exponentiell (C=10000μF
R=4000Ω)
C=10000μF
R=2000Ω
Exponentiell (C=10000μF
R=2000Ω)
C=20000μF
R=2000Ω
Exponentiell (C=20000μF
R=2000Ω)
t in s
Auswertung:
Aus dem I-t-Diagramm lässt grob die insgesamt geflossene Ladung
bestimmen.
Q
I = → Q=I⋅t
t
Q≈I 1⋅t 1+I 2⋅t 2+I 3⋅t 3+...
Q≈I 1⋅20 s+I 3⋅20 s+I 3⋅20 s+...
Q≈( I 1+I 2+I 3+...)⋅20 s
Q≈(0,0034 A+0,0024 A+0,0016 A )⋅20 s
Q≈0,213C
Aufgabe:
PC-Versuch: R=50Ω, C=0,2F, U=9V
Bestimme die geflossene Ladung Q aus dem Kondensator-Versuch am PC
einmal als Fläche unter deinem I-t-Diagramm und einmal mit der Formel
C=Q/U
Merke:
Ein Kondensator C sollte immer über einen Widerstand R geladen und
entladen werden.
Lade- und Entladestrom I ist im Verlauf exponentiell abnehmend.
Zusatz-Info:
In Schaltkreisen wird gerne ein RC-Element parallel zur Spannungsquelle
geschaltet um Spannungsspitzen aufzufangen: Wechselstrom-Baukasten
Gruppenarbeit:
Wiederholung der wichtigsten Formeln
Aufgaben:
Ende des Kapitels E-Feld als Zusammenfassung
Im 2-Stündigen Kurs nicht behandelt:
▪
Coulomb-Kraft
▪
Parallelschaltung, Reihenschaltung von Kondensatoren
▪
Flächenladungsdichte
▪
ε0 als Proportionalitätsfaktor zwischen Flächenladungsdichte und E-Feld
▪
εr in Versuch und Formel
3 Magnetismus und Teilchen
3.1 Magnete und Magnetfelder
Austeilen:
Elementarmagnetmodell
Versuch:
Zerbrochener Magnet
Aufgabe:
Zwei Eisenstäbe
Film:
Magnetisieren
Schülerversuch: Magnet-Feld
Anleitung:
▪
Falte jede Seite des Papiers ca. 2cm ein.
Knicke dann die Ecken so nach innen ein,
dass eine Schale entsteht. Evtl. kannst du die
eingeknickten Ecken innen ankleben.
▪
Nehme dir etwas Eisenpulver und verteile es
so gleichmäßig
wie möglich in der Schale. Es genügt 10% der Fläche gleichmäßig zu
bedecken. Achtung: Auf keinen Fall darf Eisenpulver an einen Magneten
kommen.
▪
Stelle nun die Schale vorsichtig über den StabMagnet.
▪
Mathe
Klopfe nun zart 2-10mal gegen die Schalte, die
Eisenspäne sollten ein Muster bilden. Vorsicht: Zu viel Klopfen und das
Pulver bildet Klumpen und Flächen, zu wenig Klopfen und man erkennt das
Muster nicht. Es sollten sich Striche und Stränge ausbilden.
Geschichte
Ergebnis:
Zeichne einen Stab-Magneten in dein Heft. Zeichne mit Bleistift das von dir
entdeckte Muster hinzu.
Für Schnelle: Wiederhole den Versuch mit einem Hufeisen-Magneten.
Film:
Feldlinien
Film:
Richtung der Feldlinie ab 6:10
Austeilen:
Feldlinien von Stab-Magnet und Hufeisen-Magnet
Merke:
Ein Magnet wirkt mit Hilfe seines Magnet-Feldes. Wir zeichnen ein MagnetFeld durch (blaue) Feldlinien ein. Diese Feldlinien laufen vom Nordpol zum
Südpol. Oder: Die Feldlinien laufen, wie ein einzelner Nordpol laufen würde
Aufgabe:
(austeilen)
Zeichne (blaue) Feldlinien ein. Beginne bei den Sternen. Laufe wie ein
Nordpol laufen würde. Zeichne bei Aufgabe 3 selbstständig das Feld ein.
Aufgabe 1
Aufgabe 2
Aufgabe 3
S
N
N
S
3.2 Strom erzeugt Magnetismus
Einstieg:
Schrottplatz-Kran. Warum ist ein „normaler Magnet“ nicht gut
Film:
Schrottkran: 24:50
Film:
Ørsted-Versuch ab 11:50
Versuch:
Ørsted-Versuch
Rings um einen Stromkabel ist ein ringartiges Magnetfeld
+
U=5V
Besser lässt sich das Magnetfeld zeichnen mit folgender Konvention:
·
Bedeutet die Elektronen kommen aus der Ebene (Tafel) heraus.
x
Bedeutet die Elektronen gehen in die Ebene (Tafel) hinein.
X
Merke:
·
Linke-Hand Regel1:
Elektronen fließen von - nach +, und werden vom linken
Daumen dargestellt. Dann verläuft um den Stromleiter ein
Magnetfeld, in Richtung der Finger
Aufgabe 1:
Magnetfeld zwei paralleler Leiter. Elektronen werden in die Bildebene hinein
geleitet. Zeichne die Magnet-Feldlinien (zunächst mit Bleistift)
x
x
Lösung:
X
X
Aufgabe 2:
Zeichne das Magnet-Feld zur folgenden Leiter-Konstellation:
·
·
x
·
x
x
Lösung:
·
·
X
X
·
X
X
Magnetfeld einer Spule
Film:
Von Ørsted bis Spule
Aufgabe 3:
Eine Leiterschleife erzeugt ein Magnet-Feld
→
Elektronen
Versuch:
Film:
-
·
·
X
+
→ Elektronen
·
X
+
a) Bestimme die Richtung des B-Feldes im ersten Bildes indem du
· oder X auswählst. (Verwende die Linke-Hand-Regel)
b)Bestimme die Richtung des ersten Bildes indem du für das B-Feld im
Inneren
oder
auswählst.(Verwende die Linke-Hand-Regel)
TODO:
Magnetfeld Wirkung der Erde auf geladenes Gas
3.3 Magnetismus verändert den Strom
Versuch:
Leiterschleifenschaukel
Film:
Leiterschaukel ab 3:00
Versuch:
Magnetfeld lenkt Elektronen-Strahl ab.
Elektronen-Strahl ab 12:30
Merke:
Linke-Hand-Regel 2: Lorenz-Kraft
Bewegen sich Elektronen senkrecht zu einem Magnetfeld, so erfahren sie
eine, erneut senkrecht stehende Kraft, die Lorenzkraft F L.
Die Richtungen lassen sich mit der Linken Hand bestimmen:
Daumen → Elektronenbewegung
Zeigefinger → Magnetfeld-Feldlinien (B-Feld)
Mittelfinger → Lorenzkraft FL
Beispiele:
(austeilen)
Mit Hilfe der dritten Dimension ( · und X ) zeichnen wir die drei Richtungen in
die Bilder ein.
Aufgabe:
Arbeitsblatt Lorenz-Kraft
3.4 Mit der Lorenz-Kraft Magnet-Felder messen
Kraft auf Leiterschaukel 3:15
Skizze:
(austeilen)
F in N:
Film:
Muss der Strom nach hinten ( · oder X )
fließen, damit der Kraftmesser nach unten
ausgelenkt wird?
Versuch:
Strom I
Kraft auf Leiterschaukel bestimmen
Ziel:
N
s
Ein Maß für das Magnetfeld, genau
genommen, die magnetische Flussdichte B
(Magnet-Feld → B-Feld)
S
Beobachtung/Bemerkung:
▪
Wir analysieren die Kraft, die auf den Leiterrahmen wirkt und nutzen diese
Kraft als Maß für das B-Feld.
▪
Die Kraft F auf den Rahmen hängt aber nicht nur vom B-Feld ab.
▪
Die Kraft F ist proportional zum Strom I durch den Leiter.
F∼I
▪
Die Kraft F ist proportional zur wirksamen Länge des Leiters s im B-Feld
F∼s (Die Skizze zeigt s=2·5cm)
▪
Ein Quotient
F
I⋅s
muss also konstant sein. Er steht somit für die stärke der
magnetischen Flussdichte B → B=
F
I⋅s
Merke:
Mit Hilfe der Lorenz-Kraft auf einen stromdurchflossenen Leiter, findet man
ein Maß für das Magnetfeld B (magnetische Flussdichte)
B=
FL
B wird in Tesla (T) gemessen.
I⋅s
Beispiel:
Ein Drahtrahmen 5cm x 5cm mit hundert Windungen erfährt bei I=0,05 A die
Kraft F=0,01N
B=
F
0,01 N
0,01 N
=
=
=0,04 T
I⋅s 0,05 A⋅(100⋅0,05 m) 0,25 Am
Versuch:
Stromric
XX
htung
N
s
S
geg.: n=100, m=0,8g, I=250mA Rahmenbreite: 5cm
Gewichtskraft von 0,8g:
m=0,8 g=0,0008 kg
FG =m⋅g=0,0008 kg⋅9,81
N
=0,00785 N
kg
m=0,8g
Stärke der des Magnet-Felds:
FG =F L
F
0,00785 N
B= L =
=0,00628 T
I⋅s 0,25 A⋅(100⋅0,05 cm)
Typische Werte:
0,00005T → Erdmagnetfeld in D*
0,01T → Spielzeug-Magnete*
0,1T → Hufeisen-Magnet*
1T → Neodym-Magnet*
0,5-3T → Kernspin-Tomograph
8,6T → Supraleiter am CERN
23T → Rekord supraleitender Magnet
*Stärke der Flussdichte B hängt natürlich vom Ort ab
Aufgaben:
Aufgabenblatt B-Feld
Aufgaben:
Aufgaben aus dem Buch S 47 A1A2
Die Hall-Sonde
Wdh:
Wie war das Experiment aufgebaut, mit dem letztlich die Stärke B der
magnetischen Flussdichte gemessen wurde? Welche Werte brauchte man
dazu alles?
Fazit:
So ein Aufbau ist zu umständliche und Fehleranfällig. Man kann den Wert B
auf einen bessere Weise messen.
3.5 Das Magnet-Feld einer Spule
Wdh:
Wir wissen schon, dass in einer Spule ein
Magnetfeld entsteht….
„Linke-Hand-Regel 1“
Film:
Von Ørsted bis Spule
Fazit:
Das Innere einer schlanken Spule ist ein homogenes
Magnet-Feld. (Außer an den Enden)
Die magnetische Flussdichte B lässt sich gut über die Stromstärke I
einstellen. Es ist eine gute Umgebung für Experimente.
Es fehlt eine Formel um die Flussdichte B in der Spule zu berechnen.
Gedanken-Experiment: (austeilen)
Durch jede der gezeigten Spulen soll die Stromstärke I=0,2A fließen, welche
der Spulen hat in ihrem inneren die größte magnetische Flussdichte B?
Tafel:
▪
Die Stärke des B-Feldes hängt von der Windungsdichte
die Anzahl der Windungen und l die Länge der Spule →
n
ab. Hierbei ist n
l
n
B∼
l
▪
Die Stärke des B-Feldes hängt von der Stromstärke I ab → B∼I
▪
Von mehr hängt B nicht ab. B hängt übrigens nicht vom Durchmesser ab.
▪
Die Formel
I
▪
n
B=I⋅ ist falsch, da B-Werte i.d.R. kleine Zahlen sind, sich
l
n
wegen der Windungsdichte aber groß wird.
l
T⋅m
heißt magnetische
A
Feldkonstante und bringt die richtigen Ergebnisse bei den Messungen.
Der Proportionalitätsfaktor
μ0=1,26⋅10−6
Merke:
Die magnetische Flussdichte einer Spule berechnet sich:
n
T⋅m
B=μ 0⋅I⋅ mit μ0=1,26⋅10−6
l
A
Beispiel:
Durch die Versuchsspule mit n=___Windungen und einer Länge von
l=___cm darf ein maximaler Strom von I=____A
Aufgabe:
Durch die herumgegebenen Spulen soll die Stromstärke I=0,1 fließen.
Bestimme die entstehende magnetische Flussdichte B
Aufgaben:
Arbeitsblatt
4Stundig:
Komponent des B-Feldes der in Richtung → cos(α)
4Stundig:
Selbstständige Bestimmung von μ0.
Versuch:
TODO
Aufgaben: