Abitur - Leistungskurs Physik Sachsen

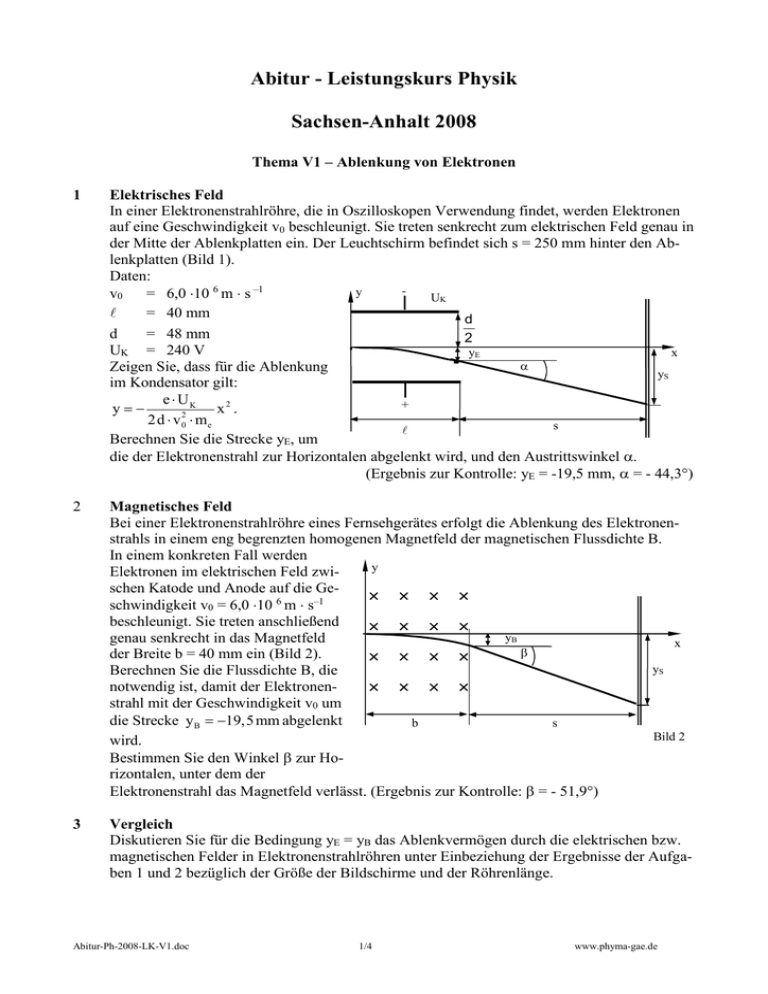
Abitur - Leistungskurs Physik
Sachsen-Anhalt 2008
Thema V1 – Ablenkung von Elektronen
1
Elektrisches Feld
In einer Elektronenstrahlröhre, die in Oszilloskopen Verwendung findet, werden Elektronen
auf eine Geschwindigkeit v0 beschleunigt. Sie treten senkrecht zum elektrischen Feld genau in
der Mitte der Ablenkplatten ein. Der Leuchtschirm befindet sich s = 250 mm hinter den Ablenkplatten (Bild 1).
Daten:
y
v0
= 6,0 10 6 m  s –1
UK

= 40 mm
d
d
= 48 mm
2
UK = 240 V
yE
x

Zeigen Sie, dass für die Ablenkung
yS
im Kondensator gilt:
e  UK
+
y
x2 .
2 d  v 20  m e
s

Berechnen Sie die Strecke yE, um
die der Elektronenstrahl zur Horizontalen abgelenkt wird, und den Austrittswinkel .
(Ergebnis zur Kontrolle: yE = -19,5 mm,  = - 44,3°)
2
Magnetisches Feld
Bei einer Elektronenstrahlröhre eines Fernsehgerätes erfolgt die Ablenkung des Elektronenstrahls in einem eng begrenzten homogenen Magnetfeld der magnetischen Flussdichte B.
In einem konkreten Fall werden
y
Elektronen im elektrischen Feld zwischen Katode und Anode auf die Ge   
schwindigkeit v0 = 6,0 10 6 m  s–1
beschleunigt. Sie treten anschließend
   
yB
genau senkrecht in das Magnetfeld
x

der Breite b = 40 mm ein (Bild 2).
   
yS
Berechnen Sie die Flussdichte B, die
notwendig ist, damit der Elektronen   
strahl mit der Geschwindigkeit v0 um
die Strecke y B  19,5 mm abgelenkt
s
b
Bild 2
wird.
Bestimmen Sie den Winkel  zur Horizontalen, unter dem der
Elektronenstrahl das Magnetfeld verlässt. (Ergebnis zur Kontrolle:  = - 51,9°)
3
Vergleich
Diskutieren Sie für die Bedingung yE = yB das Ablenkvermögen durch die elektrischen bzw.
magnetischen Felder in Elektronenstrahlröhren unter Einbeziehung der Ergebnisse der Aufgaben 1 und 2 bezüglich der Größe der Bildschirme und der Röhrenlänge.
Abitur-Ph-2008-LK-V1.doc
1/4
www.phyma-gae.de
Lösung:
1
Elektrisches Feld
Herleitung:
x-Richtung: gleichförmige Bewegung
x
x  v0  t
 1 t 
v0
y-Richtung: gleichmäßig beschleunigte Bewegung
a
y    t2
F  ma
2
F
U
a
F  EQ  Ee
mit E 
m
d
Ue
F
d
Ue
a
md
U e 2
y
t
mit  1 
2md
U e
y
 x2
2
2  m  d  v0
Berechnung der horizontalen Ablenkung:
2
240 V 1, 602 1019 As
yE  
  4, 0 10 2  m 2
2
2  9,109 1031 kg  4,8 102 m   6, 0 106  m 2  s 2
y E  0,0195 m  19,5 mm
 y 
V  As  m 2
J  m2

m
kg  m  m 2  s 2 J  m
Berechnung des Austrittswinkels:
dy
tan    
 y ' x 
dx
eUx

d  m  v0 2

240 V 1, 602 1019 As
2  9,109 10
31
kg  4,8 10 m   6, 0 10

6 2
2
m s
2
2
 4, 0 10 2 m
  44,3
oder:
tan    
y E 19,5 mm

   44,3

20 mm
2
Abitur-Ph-2008-LK-V1.doc
2/4
www.phyma-gae.de
2
Magnetisches Feld
Berechnen der Flussdichte B:
Berechnung des Radius:
2
r 2  b2   r  yB 
yB
r  b  r  2  r  yB  yB
2
2
2
2
0  b2  2  r  yB  yB2

r
b 2  yB 2
b2
 : r  2  y  2  y  y2B
B
B
2
r
r - yB
wenn berechnet: r  0, 05077 m
FZ  FL
m
v2
 evB
r
mv
B
er
mit

2
b2  yB2
2  yB
2  m  v  yB
e   b2  yB2 
B
B
b
2  9,109 1031 kg  6,0 106 m  s 1 1,95 102 m
1, 602 10
 B 
19

As   4 10

2 2
m  1,95 10
2

2 2
m
2

 6, 72 104 T  oder r eingesetzt 
kg  m  s 1  m kg  m 2  s 2
J
VAs Vs




T
2
2
2
As  m
Am
Am
A  m2 m2
Bestimmung des Ablenkwinkels:
2
r 2  b2   r  yB 
 r  yB   r 2  b2
yB  b   r  r 2  b2
2
d yB
2 b
b


2
2
2
db
2 r  b
r  b2
4 102 m

2
2
 0, 05077  m 2   4 102  m2
tan    
  51,9
oder:
1
r
sin  1  
b
40 mm

 1  51, 9
r 50,8 mm
r

90°-
   51,9 (aus Winkelrichtung)
b
Abitur-Ph-2008-LK-V1.doc
3/4
www.phyma-gae.de
3
Vergleich
Bedingung: y E  y B - Diskussion:
 Austrittswinkel  im B-Feld ist größer als Austrittswinkel  im E-Feld
 Bei festem Abstand Feld-Bildschirm wird der Elektronenstrahl bei magnetischer Ablenkung weiter abgelenkt
 größerer Bildschirm möglich
 Bei fester Bildschirmgröße kann die Röhre mit magnetischer Ablenkung kürzer sein.
Abitur-Ph-2008-LK-V1.doc
4/4
www.phyma-gae.de