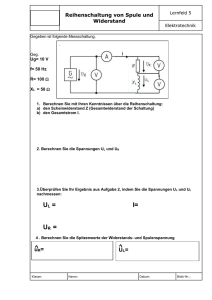
Aufgabenblatt 8 - Benutzer-Homepage

Prof. Dr. Th. Letschert
FB MNI
TH Mittelhessen
StudiumPlus
Informatik II
Aufgabenblatt 8
Gruppenübung
Aufgabe 1
In Aufgabe 5 und 6 von Aufgabenblatt 4 haben Sie Schaltkreise mit Widerständen, Reihenschaltungen oder Parallelschaltungen modelliert. In den Modellen kann der Stromfluss bei angelegten Spannungen berechnet werden.
Erstellen Sie ein neues Projekt mit den den entsprechenden (alten) Klassen.
Zur Erinnerung:
public class Widerstand {
private double r; // Widerstandswert in Ohm
public Widerstand(double ohm) {
this.r = ohm;
}
public double getR() {
return r;
}
}
package schaltung;
public class Parallelschaltung {
private Widerstand w1;
private Widerstand w2;
private double u = 0.0; // Spannung in Volt
public Parallelschaltung(Widerstand w1, Widerstand w2) {
this.w1 = w1;
this.w2 = w2;
}
public double getR() {
return 1.0/(1.0/w1.getR()+1.0/w2.getR());
}
public void setU(double u) {
this.u = u;
}
public double getI() {
return this.u / getR();
}
}
package schaltung;
public class Reihenschaltung {
private Widerstand w1;
private Widerstand w2;
private double u = 0.0;
public Reihenschaltung(Widerstand w1, Widerstand w2) {
this.w1 = w1;
this.w2 = w2;
}
public double getR() {
return w1.getR()+w2.getR();
}
public void setU(double u) {
this.u = u;
}
public double getI() {
return this.u / getR();
}
}
Damit können nun Parallel– und Reihenschaltungen modelliert werden:
package schaltung;
public class Main {
public static void
Widerstand
Widerstand
Widerstand
Widerstand
main(String[] args) {
r1 = new Widerstand(50);
r2 = new Widerstand(100);
r3 = new Widerstand(150);
r4 = new Widerstand(300);
Reihenschaltung c1 = new Reihenschaltung(r1, r2);
Parallelschaltung c2 = new Parallelschaltung(r3, r4);
// Widerstand berechen
System.out.println(c1.getR());
System.out.println(c2.getR());
// Spannung anlegen
c1.setU(50.0);
c2.setU(50.0);
// Stromfluss berechnen
System.out.println(c1.getI());
System.out.println(c2.getI());
}
}
Aufgabe 2
Eigentlich müssten sich Reihen– und Parallelschaltungen selbst wieder zu neuen Schaltungen verknüpfen lassen.
Also beispielsweise:
Widerstand
Widerstand
Widerstand
Widerstand
r1
r2
r3
r4
=
=
=
=
new
new
new
new
Widerstand(50);
Widerstand(100);
Widerstand(150);
Widerstand(300);
Reihenschaltung sr1 = new Reihenschaltung(r1, r2);
Reihenschaltung sr2 = new Reihenschaltung(r3, r4);
Parallelschaltung sp = new Parallelschaltung(sr1, sr2);
Warum funktioniert das nicht? – Richtig, weil Parallelschaltung keinen entsprechenden Konstruktor hat.
Erstellen Sie den passenden Konstruktor. Beispielsweise als:
2
private Widerstand w1;
private Widerstand w2;
private double u = 0.0; // Spannung in Volt
private Reihenschaltung sr1; // neu
private Reihenschaltung sr2; // neu
public Parallelschaltung(Widerstand w1, Widerstand w2) {
this.w1 = w1;
this.w2 = w2;
}
// neu:
public Parallelschaltung(Reihenschaltung sr1, Reihenschaltung sr2) {
this.sr1 = sr1;
this.sr2 =sr2;
}
Hmm – warum ist mehr als unbefriedigend? Müssten sr1 und sr2 nicht eigentlich in w1 und in w2 gespeichert
werden, denn es sind ja eigentlich die “Widerstände” die die parallel geschaltet werden sollen.
Warum geht das nicht – Warum kann sr1 und sr2 nicht in w1 und w2 gespeichert werden? Oder geht das eventuell
doch?
Aufgabe 3
Irgendetwas haben wir falsch gemacht. Wir haben mit Widerstand eine Klasse definiert, die ein irgendwie
geartetes Ding modelliert, das einen Widerstand hat. Das ist aber nicht präzise genug. Wir haben hier versucht
zwei Dinge zu mischen:
• Widerstände als elementare elektronische Bauelemente.
• Widerstände als etwas das einen Widerstand hat. Beispielsweise eine Schaltung.
Beides ist eng verwandt aber nicht das gleiche. Einer der beiden Begriffe ist allgemeiner, umfassender als der
andere. Welcher?
Aufgabe 4
Wir unterscheiden Widerstände als elementare Bauelemente und Widerstände als “Ding mit einem Widerstand”.
Der Einfachheit halber nehmen wir als Bauelement mit Widerstand eine Spule (wir haben es nur mit Gleichstrom
zu tun):
public class Spule {
private double r; // Widerstandswert in Ohm
public Spule(double ohm) {
this.r = ohm;
}
public double getR() {
return r;
}
}
Als Eigenschaft aller Dinge mit einem Widerstand definieren wir:
public interface Widerstand {
public double getR();
}
3
Um auszudrücken, dass eine Spule ein Ding mit einem Widerstand ist, muss die Definition der Spule geändert
werden:
public class Spule implements Widerstand {
. . .
}
Um kenntlich zu machen, dass getR eine Methode ist, die von der Eigenschaft ein Widerstand zu sein
(implements Widerstand) erzwungen wird, kann sie mit Override annotiert werden:
public class Spule implements Widerstand {
. . .
@Override
public double getR() {
return r;
}
}
Jetzt können wir sagen, dass Reihen– und Parallelschaltungen aus Dingen mit einem Widerstand zusammengesetzt
werden können und selbst einen Widerstand haben:
public class Reihenschaltung implements Widerstand {
private Widerstand w1;
private Widerstand w2;
private double u = 0.0;
public Reihenschaltung(Widerstand w1, Widerstand w2) {
this.w1 = w1;
this.w2 = w2;
}
@Override
public double getR() {
return w1.getR()+w2.getR();
}
public void setU(double u) {
this.u = u;
}
public double getI() {
return this.u / getR();
}
}
public class Parallelschaltung implements Widerstand {
private Widerstand w1;
private Widerstand w2;
private double u = 0.0; // Spannung in Volt
public Parallelschaltung(Widerstand w1, Widerstand w2) {
this.w1 = w1;
this.w2 = w2;
}
@Override
public double getR() {
return 1.0/(1.0/w1.getR()+1.0/w2.getR());
}
public void setU(double u) {
this.u = u;
}
public double getI() {
return this.u / getR();
4
}
}
Damit können jetzt beliebig komplexe Schaltungen definiert werden:
public class Main {
public static void
Widerstand
Widerstand
Widerstand
Widerstand
main(String[] args) {
r1 = new Spule(50);
r2 = new Spule(100);
r3 = new Spule(150);
r4 = new Spule(300);
Reihenschaltung sr1 = new Reihenschaltung(r1, r2);
Reihenschaltung sr2 = new Reihenschaltung(r3, r4);
Parallelschaltung sp = new Parallelschaltung(sr1, sr2);
System.out.println(sp.getR());
sp.setU(50.0);
System.out.println(sp.getI());
}
}
Aufgabe 5
Zeichen Sie ein UML–Klassendiagramm das die Definitionen von Aufgabe 4 darstellt.
Aufgabe 6
Spannungen und Ströme in einem Schaltnetz können mit Hilfe der Kirchhoffchen Regeln analysiert werden. Wir
können damit also nicht nur den Strom bei einer angelegten Spannung für die Gesamtschaltung berechnen, sondern
auch für alle Teilschaltungen. Geben Sie informal (kein Code, nur Worte und Beispiele) einen Algorithmus an, mit
dem zu einer vorgegebenen Spannung für eine (Zweipol-) Schaltung, Spannung und Strom für jede Teilschaltung
berechnet werden kann.
Aufgabe 7
Sie haben als Lösung zu Aufgabe 6 sicher in etwa folgenden Algorithmus definiert:
1. Berechne den Gesamtwiderstand R des Schaltkreises (wie oben).
2. Berechne aus R und der angelegten Spannung U den Strom I = U/R der durch den Schaltkreis fließt.
3. Handelt es sich sich bei dem Stromkreis um eine Spule, dann ist die Aufgabe erledigt.
4. Handelt es sich um eine Parallelschaltung, dann verteile Spannung U und Strom I nach folgender Regel
auf die Teilschaltungen t:
• Die Spannung Ut ist in jedem Teilschaltkreis tgleich der Gesamtspannung Ut = U.
• Der Strom It in jedem Teilschaltkreis t entspricht seinem Anteil am Gesamtwiderstand. It = U/Rt
5. Handelt es sich um eine Reihenschaltung, dann verteile Spannung U und Strom I nach folgender Regel auf
die Teilschaltungen t:
• Der Strom It ist in jedem Teilschaltkreis tgleich dem Gesamtstrom It = I.
• Die Spannung Ut in jedem Teilschaltkreis t entspricht seinem Anteil am Gesamtwiderstand. Ut = I ∗ Rt
5
Dieser Algorithmus kann auf vielerlei Arten implementiert werden. Hier soll es “objektorientiert” und mit Vererbung geschehen: U, I und R sollen Eigenschaften aller Schaltkreise und Teilschaltkreise sein:
1. R ergibt sich aus der Zusammensetzung des Schaltkreises.
2. U wird für den Gesamtschaltkreis zunächst auf 0 gesetzt und kann dann von außen verändert werden.
3. I wird für den Gesamtschaltkreis aus U und R berechnet.
4. U und I für die Teilschaltkreise werden entsprechend der Kirchhoffchen Regeln aus U, I und R berechnet.
Wir streben eine Lösung an, bei der eine Zweipolschaltung definiert und mit einer Spannungsquelle verbunden
werden kann. Etwa so:
package aufgabe_7;
public class Test {
public static
Zweipol
Zweipol
Zweipol
void
r1 =
r2 =
r3 =
main(String[] args) {
new Spule(10);
new Spule(30);
new Spule(20);
Zweipol ps = new Parallelschaltung(r2, r3);
Zweipol rs = new Reihenschaltung(r1, ps);
Spannungsquelle quelle = new Spannungsquelle();
quelle.setZweipolSchaltkreis(rs);
quelle.setU(220);
System.out.println("R1:
System.out.println("R2:
System.out.println("R3:
System.out.println("PS:
System.out.println("RS:
R="
R="
R="
R="
R="
+
+
+
+
+
r1.getR()
r2.getR()
r3.getR()
ps.getR()
rs.getR()
+
+
+
+
+
"
"
"
"
"
U=
U=
U=
U=
U=
"
"
"
"
"
+
+
+
+
+
r1.getU()
r2.getU()
r3.getU()
ps.getU()
rs.getU()
+
+
+
+
+
"
"
"
"
"
I=
I=
I=
I=
I=
"
"
"
"
"
+
+
+
+
+
}
}
Für einen Test berechnen das erwartete Ergebnis “händisch”:
R1:
R2:
R3:
PS:
RS:
R=10.0
R=30.0
R=20.0
R=12.0
R=22.0
U=
U=
U=
U=
U=
100.0
120.0
120.0
120.0
220.0
I=
I=
I=
I=
I=
10.0
4.0
6.0
10.0
10.0
Eine einfache Spannungsquelle ist schnell definiert:
package aufgabe_7;
/**
* Eine Spannungsquelle liefert eine Spannung an einen angeschlossenen Zweipol.
*/
public class Spannungsquelle {
private Zweipol zweipol;
/**
* Verbinde die Spannungsquelle mit einem Schlatkreis.
* @param zweipol
*/
public void setZweipolSchaltkreis(Zweipol zweipol) {
this.zweipol = zweipol;
}
/**
* Veranlasse die Erzeugung einer Spannung.
* @param u Spannung in Volt
*/
6
r1.getI());
r2.getI());
r3.getI());
ps.getI());
rs.getI());
public void setU(double u) {
if (zweipol != null) {
double r = zweipol.getR();
double i = u/r;
zweipol.kirchhoff(u, i);
}
}
}
Wird eine Spannung gesetzt, dann wird für den angeschlossenen Zweipol zuerst der Widerstand berechnet, dann
der fließende Strom und schließlich werden die Kirchhoffschen Gesetze im Zweipol angewendet.
Ein Zweipol ganz allgemein wird mit einer abstrakten Klasse modelliert:
package aufgabe_7;
/**
* Basisklasse der Zweipolschaltungen.
*/
public abstract class Zweipol {
//---------------------------------------------------------------------------------// oeffentliche Schnittstelle
/**
* @return Gesamtwiderstand in Ohm
*/
public double getR() { return computeR(); }
/**
* @return aktuelle Gesamtspannung in Volt
*/
public double getU() { return u; }
/**
* @return aktueller Stromfluss in Ampere
*/
public double getI() { return i; }
//----------------------------------------------------------------------------// Methoden die von den Ableitungen zu liefern sind
/**
* Berechne den Widerstand des Zweipols
* @return Widerstand in Ohm
*/
protected abstract double computeR();
/**
* Wende die Kirhoffschen Regeln an zur Berechnung der Spannungen und Stroeme
* in den Unterschaltkreisen.
* Default-Implementierung: tue nichts.
* @param u aktuelle Gesamtspannung
* @param i aktueller Gesamtstrom
*/
protected void applyKirchhoff(double u, double i) {}
/**
* Wende die Kirchhoffsche Regeln zur Berechnung der
* an zur Berechnung der Spannungen und Stroeme in den Unterschaltkreisen.
* @param u aktuelle Gesamtspannung
* @param i aktueller Gesamtstrom
*/
public void kirchhoff(double u, double i) {
this.u = u;
this.i = i;
applyKirchhoff(u, i);
}
//-----------------------------------------------------------------------------
7
// Private Komponenten
// (sind in jeder Instanz jeder Ableitung vorhanden aber nicht von aussen zugreifbar)
private double u; // aktuelle Spannung
private double i; // aktueller Strom
// der aktuelle Widerstand wird nicht in jedem (Teil-) Schaltkreis gespeichert
// sondern stets berechnet.
}
Über die öffentliche Schnittstelle (public–Methoden) können die aktuellen Widerstands-, Spannungs, und Stromwerte abgefragt werden.
Die Ableitungen haben die Methoden zur Berechnung des Widerstands und zur Anwendung der Kirchhoffschen
Regeln zu liefern. (abstract protected–Methoden)
Jede Instanz einer Ableitung speichert die aktuelle Spannung und den aktuellen Strom. (private–Komponenten)
Der Widerstand wird im Gegensatz zu Spannung und Strom nicht in Instanzen dieser Klasse gespeichert. Das ist
eine willkürliche Entwurfsentscheidung, die auf der Intuition basiert, dass nur Spulen “wirklich” einen Widerstand
haben.
Spulen stellen die elementaren Zweipole dar:
package aufgabe_7;
/**
* Instanzen dieser Klasse modellieren Spulen
* im Gleichstrom. (Eigentlich Ohmsche Widerstaende)
*
*/
public class Spule extends Zweipol {
public Spule(double r) {
this.r = r;
}
@Override
protected double computeR() {
return r;
}
private double r; // Widerstand in Ohm;
}
Die Kirchhoffsche Regel wird nicht neu implementiert. Somit wird die Default–Implementierung der Basisklasse
(tue nichts) übernommen.
Parallelschaltungen sind Zweipole, bei den die Kirhoffsche Regel angewendet werden muss:
package aufgabe_7;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* Instanze dieser Klasse modellieren Reihenschaltungen.
*
*/
public class Reihenschaltung extends Zweipol {
public Reihenschaltung (Zweipol... komponenten) {
this.komponenten = Arrays.asList(komponenten);
}
@Override
protected double computeR() {
double r = 0.0;
for (Zweipol s: komponenten) {
r = r + s.getR();
8
}
return r;
}
@Override
protected void applyKirchhoff(double u, double i) {
for (Zweipol zp: komponenten) {
zp.kirchhoff(i*zp.getR(), i);
}
}
private List<Zweipol> komponenten = new ArrayList<>();
}
Parallelschaltungen sind den Reihenschaltungen sehr ähnlich:
package aufgabe_7;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* Instanze dieser Klasse modellieren Parallelschaltungen.
*
*/
public class Parallelschaltung extends Zweipol {
public Parallelschaltung (Zweipol... komponenten) {
this.komponenten = Arrays.asList(komponenten);
}
@Override
protected double computeR() {
double r = 0.0;
for (Zweipol s: komponenten) {
r = r + 1.0/s.getR();
}
return 1.0/r;
}
@Override
protected void applyKirchhoff(double u, double i) {
for (Zweipol zp: komponenten) {
zp.kirchhoff(u, u/zp.getR());
}
}
private List<Zweipol> komponenten = new ArrayList<>();
}
1. Zeichen Sie ein UML–Diagramm der Definitionen.
2. Implementieren und testen Sie den Code.
Aufgabe 8
Reihenschaltung und Parallelschaltungen sind sich sehr ähnlich. Das Ähnliche unterschiedlicher Klassen kann in
einer Basisklasse zusammengefasst werden. Tun Sie dies. Definieren Sie eine Basisklasse KomplexeSchaltung in
der die Gemeinsamkeiten von reihen– und Parallelschaltungen zusammengefasst sind. Vereinfachen Sie dann die
Klassen zur Modellierung von Reihen- und Parallelschaltungen.
Diskutieren Sie die Sinnhaftigkeit dieser Modifikation. Was spricht dafür, was dagegen?
9
Hausaufgaben
Aufgabe 9
Übertragen Sie die das Programm auf sinusförmige Wechselstromnetze mit ohmschen Widerständen, Impedanzen
und Kapazitäten. Neben der Spannung soll auch die Frequenz gesetzt werden können.
Hinweis: Arbeiten Sie mit komplexen Zahlen. Definieren Sie dazu eine Klasse Komplex mit der die Rechnungen
bequem ausgeführt werden können.
Abgabe Lösungen können in Gruppen von bis zu 4 Mitgliedern erarbeitet werden. Die Lösungen werden am
26. 6. 2012 inklusive einer Erklärung der relevanten elektrotechnischen Grundlagen und deren Umsetzung präsentiert. Die Präsentation muss ein Klassendiagramm in UML umfassen. Bitte geben den lauffähigen Code vorher per
EMail ab (bis zum 25. 6. 2012, 24 Uhr).
10