RLC-Schaltungen

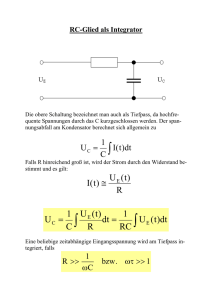
RCL - Netzwerke
Martin Adam
2. November 2005
Inhaltsverzeichnis
1 Versuchsbeschreibung
1.1 Ziel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Aufgaben . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
2
2
2 Vorbetrachtungen
2.1 RC-Glied . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Wien-Brücke . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
3
3
3 Durchführung
3.1 RC-Glied . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Kompensierter Spannungsteiler . . . . . . . . . . . . . . . . . . .
3.3 Wien-Brücke . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
5
5
7
4 Auswertung
10
1
1
Versuchsbeschreibung
1.1
Ziel
Einführung in das Verhalten passiver Wechselstromnetzwerke sowie vertraut
machen mit Eigenschaften der im Elektronikpraktikum vorhandenen Messtechnik. Wiederholung der im Grundpraktikum erworbenen Kenntnisse und Fertigkeiten und Festigung der Berechnung von Wechselstromnetzwerken. Vorbereitung der folgenden Experimente.
1.2
Aufgaben
1. RC-Glied:
Bei Einspeisung einer Rechteckimpulsfolge (Impulsdauer ti ) sind Ue , UC
und UR für den Fall 3 · RC = ti zu messen. Die Zeitverläufe sind auszudrucken. Aus der Grafik ist die Zeitkonstante τ zu ermitteln.
2. Kompensierter Spannungsteiler:
Bauen Sie einen frequenzkompensierten Spannungsteiler auf, der die Eingangsspannung im Verhältnis 5:1 teilt. Gleichen Sie ihn mit Rechteckimpulsen ab. Drucken Sie die Zeitverläufe von Ue und Ue sowie das Fourierspektrum der Ausgangsspannung bei Kompensation sowie Über- und
Unterkompensation aus.
3. Wien-Brücke:
Bauen Sie einen Wien-Brücken-Zweig auf. Ermitteln Sie, bei welchen Frequenzen die Phasenverschiebung ϕ = 45◦ , ϕ = −45◦ und ϕ = 0◦ ist.
|Ua |
.
Bestimmen Sie bei diesen Frequenzen das Übertragungsverhalten
|Ue |
2
Vorbetrachtungen
Als Impulse werden in der Inpulstechnik alle Signale bezeichnet, die sich nicht
durch mathematisch einfache, stetige Funktionen beschreiben lassen. Zum Beispiel eine Rechteckspannung lässt sich nur abschnittsweise durch stetige Funktionen beschreiben. Sie besteht aus einer Überlagerung mehrerer sinusförmiger Funktionen. Zur vollständigen Beschreibung muss man Fourier-Reihen und
Fourier-Integrale anwenden, dies liefert dann das Spektrum der Rechteckspannung. Hinsichtlich ihres Einflusses auf die Impulsübertragung lassen sich elektrische Netzwerke in zwei große Gruppen unterteilen, Hochpässe und Tiefpässe.
Ein Tiefpass überträgt bis zu einer bestimmten oberen Grenzfrequenz
ωg =
1
,
τ
τ =R·C
nur tiefe Frequenzen, einschließlich Gleichstrom. Da ein Tiefpass die in einem
Impuls steckenden hohen Frequenzen nicht durchlässt, wird er senkrechte Spannungssprünge und scharfe Ecken im Spannungsverlauf verschleifen.
2
Ein Hochpass hingegen lässt nur hohe Frequenzen durch und keinen Gleichstrom. Es werden waagerechte Teile einer Spannungskurve schlecht oder gar
nicht übertragen, weil im waagerechten Teil gewissermaßen die Gleichspannungskomponente steckt. Es entstehen sogenannte Dachschrägen.
Tiefpass:
RC-Glieder und LR-Glieder sind die einfachsten Übertragungsschaltungen für Tiefpässe. Im LR-Glied kann der Strom niemals sprunghaft, sondern nur exponentiell steigen (Selbstinduktivität der Spule). Demzufolge wird die Spannung an R ebenfalls exponentiell ansteigen, da I ∼ U . Im
RC-Glied ist die Ausgangsspannung Ua mit der Spannung UC am Kondensator identisch. Diese kann erst nach Maßgabe des Zuflusses von Ladungen an C
steigen. Somit ist der senkrechte, sprunghafte Spannungsanstieg verschliffen.
Hochpass:
CR-Glieder und RL-Glieder sind die einfachsten Übertragungsschaltungen für Hochpässe. Im CR-Glied stellt der ungeladene Kondensator eine Art Kurzschluss dar. Beim Anlegen einer Rechteckspannung nimmt er
im ersten Moment einen großen Strom auf (Ladungsstrom). Dieser Strom führt
am Widerstand R zum gleichen Spannungsverlauf mit steilem Spannungssprung
und exponetiellem Abklingen. In der RL-Glied-Schaltung wird beim Anlegen einer Rechteckspannung die ganze Spannung auch an der Spule L anliegen, jedoch
wird sie exponentiell abnehmen und somit eine Dachschräge aufweisen.
2.1
RC-Glied
In Aufgabe 1 wird ein RC-Glied verwendet. Daher erfolgt dazu ein größeres
Augenmerk aus mathematischer Sicht:
UR
UC
τ
= U0 e−t/τ
= U0 (1 − e−t/τ )
= R·C
(1)
(2)
Die charakteristischen Eigenschaften der e−t/τ -Kurve bestehen einmal darin,
dass die Kurve nach jeweils 0, 7τ in ihrer Ordinate auf die Hälfte des Ausgangswertes gefallen ist und die Anfangstangente die Neigung −1/τ hat und daher
bei t = τ durch die Abszissenachse geht.
2.2
Wien-Brücke
Die Wien-Brücke ist eine Reihenschaltung von Hoch- und Tiefpass. Daher wird
die Ausgangsspannung für hohe und tiefe Frequenzen Null. Wie groß die Ausgangsspannung bei mittleren Frequenzen wird und welche Phasenverschiebun-
3
gen auftreten kann man folgendermaßen berechnen:
→
ζ1
= R+
1
ζ2
=
Ua
Ue
=
1
jωC
1
+ jωC
R
1
R
1
+ jωC
1
1
+R+
jωC
+ jωC
jωRC
(jωRC + 1)2 + jωRC
1
R
Ua
Ue
=
Zur Vereinfachung der Rechung führt man RC =
wird ωRC = Ω:
Ue
Ua
2
Ue Ua =
=
1
ω
und
= Ω ein. Somit
ω0
ω0
Ω2 − 1
(jΩ + 1)2 + jΩ
=3+j
jΩ
Ω
2
2
ˆ
Ue
(Ω − 1)
=9+
ˆ
Ω2
Ua
(3)
1
Die Ausgangsspannung wird maximal für Ω = 1, d.h. für ω = ω0 = RC
. Bei der
1
Resonanzfrequenz wird Uˆa = 3 Uˆe , die Phasenverschiebung wird Null. Mittels
Gleichung (3) kann man die Phasenverschiebung berechnen:
tan(−ϕ)
=
Ω2 − 1
3Ω
ϕ
=
arctan
4
1 − Ω2
3Ω
3
3.1
Durchführung
RC-Glied
Abbildung 1: Schaltplan 1
Die Schaltung wurde gemäß Abbildung 1 aufgebaut und es wurde die Eingangsspannung Ue sowie die Spannung am Kondensator UC gemessen und die
Spannung am Widerstand UR vom Oszilloskop berechnen lassen. UR = Ue −UC .
Die Zeitkonstante τ wurde wie in der Vorbetrachtung mittels Anfangstangente
aus der Abbildung 1 aus dem Anhang bestimmt. Daraus ergibt sich
τ = 78µs
Der Cursor im Bild wurde zuvor absichtlich auf diese Stelle gefahren, um so die
Zeit besser bestimmen zu können. Mehr dazu in der Auswertung.
3.2
Kompensierter Spannungsteiler
Die Schaltung wurde gemäß Abbildung 2 aufgebaut. Mittels regelbarem Widerstand wurden die Spannungen 5:1 abgeglichen und mittels Ändern der Kapazität
wurde Kompensation, Unter- und Überkompensation erzielt.
Abbildung 2: Kompensation
5
Abbildung 3: Kompensation
Abbildung 4: Überkompensation
6
Abbildung 5: Unterkompensation
3.3
Wien-Brücke
Die Abbildung Wien-Brücke liefert den Schaltplan zur Messanordnung.
Abbildung 6: Wien-Brücke
7
Abbildung 7: Phase 0
Abbildung 8: Phase 44,25
Zu den gemessenen Frequenzen zu bestimmten
Phasenverschiebungen kann
Ue man nun das Übertragungsverhalten Ua bestimmen. Die Spannungen wurden
mit dem Oszillographen über Peak-to-peak-Messung bestimmt.
8
Abbildung 9: Phase -44,78
ϕ in
◦
-44,78
0,00
44,25
f in kHz
Ua in V
Ue in V
Ua
Ue
0,488
1,589
5,590
1,625
2,313
1,625
7,062
7,125
7,062
0,23
0,32
0,23
Tabelle 1: Frequenz zur Phase
9
4
Auswertung
RC-Glied:
Zum Vergleich wurde τ berechnet:
τ = R · C = 3kΩ · 27nF = 81µs
Die Abweichung von 3µs liegt größtenteils darin, dass τ = 78, 8µs mittels eingezeichneter Tangente ermittelt wurde. Die Stellung des Cursors ist ebenfalls nur
eine grobe Schätzung, dennoch liegt der ermittelte Wert dicht am berechneten.
Kompensierter Spannungsteiler: Anhand der Grafen ist sehr gut zu erkennen, dass bei Kompensation das Fourierspektrum nur aus den Oberschwingungen besteht. Bei der Überkompensation ist in der Ausgangsspannung überschwingt die steigende Flanke, der Grund ist im Fourierspektrum zu erkennen.
Es sind dort noch weitere Schwingungen zu erkennen. Geht man in Richtung
der Unterkompensation, wird das Spektrum schmaler und kleiner.
Wien-Brücke: Eine Wien-Brücke lässt, wie schon in der Vorbetrachtung erwähnt, keine hohen und keine tiefen Frequenzen durch. Man kann anhand der
Messung dieses erahnen, da für ϕ = 0◦ das Übertragungsverhältnis am größten
ist und zu ϕ = ±45◦ abfallen.
10