Protokoll Elektronikpraktikum – Versuch 2 am

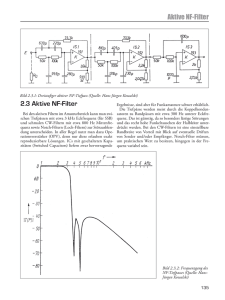
Protokoll Elektronikpraktikum – Versuch 2 am 30.04.2013
Intsar Bangwi & Sven Köppel
Passive Bauelemente
Elektronische Bauelemente stellen Einzeleinheiten von elektrischen Schaltungen da. Sie
werden mit versch. Symbolen gekennzeichnet und haben unterschiedliche Funktionen.
Demnach bilden mehrere in Reihe und/oder parallel geschaltete Bauelemente eine
Schaltung dar.
Elektrische Bauelemente werden außerdem kategorisiert unter „aktive“ und „passive“
Bauelemente. Die im Versuch verwendeten Bauelemente gehören zu den passiven
Bauelementen und zeichnen sich dadurch aus, dass diese keine verstärkende Wirkung (wie
z.B. Transistoren) oder auch steuernde Wirkung (wie z.B. Dioden, Relais) zeigen.
Bei den passiven Bauelementen handelt es sich um reelle Bauelemente wie der ohmsche
Widerstand „R“, die Induktivität „L“ und die kapazität „C“.
Kondensator im Wechselstromkreis
Der Kondensator weist im Wechselstromkreis eine besonderheit auf. Der Wechselstrom
führt dazu, dass die Strom und Spannungskennlinien Phasenverschoben sind. Die Spannung
hat einen sinusförmigen Verlauf, während der Strom einen cosinusförmigen Verlauf
beginnend mit dem Maximalwert aufzeigt.
Für die Quellenwechselspannung gilt
𝑈(𝑡) = 𝑈𝑚𝑎𝑥 ∗ 𝐬𝐢𝐧⁡(𝜔𝑡)
Für den Strom und Kondensator gilt
𝐼 = 𝑄̇
𝑄(𝑡) = 𝐶 ∗ 𝑈(𝑡)
Eingesetzt ergibt das für die Stromstärke:
𝐼(𝑡) = 𝐶 ∗
𝑑(𝑈𝑚𝑎𝑥 ∗ sin(𝜔𝑡))
= ⁡𝐶 ∗ 𝑈𝑚𝑎𝑥 ∗ 𝜔 ∗ 𝐜𝐨𝐬⁡(𝜔𝑡)
𝑑𝑡
Es lässt sich festhalten, dass sich Strom und Spannung proportional zueinander verhalten
und dass die Stromstärke proportional zur Frequenz ist.
Betrachtet man Strom und Spannung ohne die Phasenlage, so lässt sich analog zu 𝑅 =
𝑈
𝐼
für
den Wechselstromwiderstand festhalten:
𝑋𝐶 =
𝑈
1
=
𝐼 𝜔∙𝐶
Die sin/cos Abhängigkeit von Strom und Spannung lässt sich mit Hilfe eines Zeigerdiagramms
anschaulich darstellen.
Die Zeiger rotieren gegen den Uhrzeigersinn. Die y-Achse zeigt den Wert des jeweiligen
Zeigers an. Ist wie im Bild oben U=0 so ist wie man sieht der Strom maximal. Drehen sich die
Zeiger aufgrund der Spannungsänderung, so ändern sich auch die Maximalwerte der Zeiger.
RC-Glied und CR-Glied als Frequenzfilter
Der Versuch behandelt u.a. das frequenzabhängige Übertragungsverhalten des Signals im
Hoch- bzw. Tiefpass. Beschrieben wird das Verhalten durch die Übertragungsfunktion
𝐹(𝜔) =
𝑈𝐴 (𝜔)
𝑈𝐸 (𝜔)
1
𝑍𝐶
1
𝑖𝜔𝐶
=
=
=
⁡𝑓ü𝑟⁡𝑅𝐶 − 𝐺𝑙𝑖𝑒𝑑⁡
𝑅 + 𝑍𝐶 𝑅 + 1
𝑖𝜔𝜏 + 1
𝑖𝜔𝐶
𝑏𝑧𝑤.⁡⁡ =
𝑅
𝑅
𝑖𝜔𝜏
=
=
⁡⁡𝑓ü𝑟⁡𝐶𝑅 − 𝐺𝑙𝑖𝑒𝑑
𝑅 + 𝑍𝐶 𝑅 + 1
𝑖𝜔𝜏 + 1
𝑖𝜔𝐶
welche das Verhältnis von Ausgangsspannung zu Eingangsspannung beschreibt.
Tiefpass: Das RC-Glied als Frequenzfilter entspricht dem „Tiefpass“. Wichtige Kenngröße für
den Tiefpass ist die Eckfrequenz 𝒇𝑬 , welche dem Kehrwert der Zeitkonstante 𝜏 entspricht.
𝒇𝑬 =
1
1
=
⁡⁡⁡⁡(1)
𝜏 𝑅𝐶
Alle Frequenzen im RC-Glied, welche unterhalb der Eckfrequenz liegen, werden ungedämpft
übertragen -> „Tiefpass“.
Über die komplexe Übertragungsfunktion lässt sich mit (1) der Betrag der
1
Übertragungsfunktion |𝐹(𝜔)| =
√1+
𝜔 = 𝜔𝐸 gleich 𝑭(𝝎) =
𝟏
𝜔²
𝜔𝐸 ²
der Amplitudengang bestimmen. Dieser wird für
. Dies entspricht einer Dämpfung von -3dB. Steigt die Frequenz, so
√𝟐
wird auch das Signal stärker gedämpft, da der leere Kondensator durch den Widerstand des
R-Glied erst geladen werden muss. Bei Änderung der „Polung“ wird der Kondensator
entladen und das Signal „verschluckt“. Es kommt außerdem zu einer Phasenverschiebung,
𝝎
welche sich aus 𝝋 = −𝐚𝐫𝐜𝐭𝐚𝐧⁡(𝝎 ) berechnen lässt, sofern die Eckfrequenz 𝜔 bekannt ist.
𝑬
Hochpass: Das CR-Glied entspricht dem „Hochpass“. Hier ist der Ausgangsstrom abhängig
von dem Strom den der Kondensator ermöglicht. Steigt die Ladung, so wird die das
Ausgangssignal gedämpft bzw. „gesperrt“. Bei hohen Frequenzen kommt es nicht zu großen
Auf- und Abladungen, da die Stromrichtung schnell Wechselt. Der Strom passiert den
Kondensator gegen den sog. „Wechselstromwiderstand“.
Bei tiefen Frequenzen sperrt der Kondensator, da dieser längere Zeit in eine Richtung
geladen wird, und während es anschließend entlädt, die Auf- und Abladung in die
entgegengesetzte Richtung schon beginnt.
Dezibel dB
Die Verstärkung oder auch die Abschwächung wird in „Dezibel“ (dB) oder auch „Bel“ (B)
gemessen. Definiert wird diese über das Verhältnis von Ausgangslistung zu Eingangsleistung:
𝑉 = 𝑙𝑜𝑔 (
Mit 𝑃𝐴 =
|𝑈𝐴 |
𝑅
und 𝑃𝐸 =
|𝑈𝐸 |
𝑅
𝑃𝐴
𝑃𝐴
) ∙ 𝐵𝑒𝑙 = 10 ∙ 𝑙𝑜𝑔 ( ) ∙ 𝑑𝐵
𝑃𝐸
𝑃𝐸
folgt
𝑉 = 20 ∙ log⁡(
|𝑈𝐴 |
)
|𝑈𝐸 |
Bodediagramm
Das Bodediagramm besteht aus zwei Diagrammen, die Amplitude gegen die
Übertragungsfunktion aufgetragen bzw. die Phasenverschiebung gegen die
Übertragungsfunktion. Trägt man im Bodediagramm Messwerte für RC und CR Glieder ein
und nähert die Kurven, so lässt sich an den Schnittpunkten zweier Geraden die Eckfrequenz
herauslesen und bestimmen. Beispiele solcher Bodediagramme finden sich im Anhang.
Aufgaben
zu 1. Aufnahme des Bode-Diagramms für RC- und CR-Glied
Frequenz f
10 Hz
100 Hz
1 kHz
6 kHz
10 kHz
100 kHz
200 kHz
300 kHz
Eingang 𝑼𝑬
10 𝑉𝑝𝑝
10 𝑉𝑝𝑝
10 𝑉𝑝𝑝
10 𝑉𝑝𝑝
10 𝑉𝑝𝑝
10 𝑉𝑝𝑝
10 𝑉𝑝𝑝
10 𝑉𝑝𝑝
Amplitude 𝑼𝑨
10 V
10 V
3V
320 mV
160 mV
120 mV
Phase
18°
43°
72°
72°
72°
96°
Der Anhang zu dieser Aufgabe besteht aus zwei DinA4-Millimeterpapierzetteln. Auf dem
ersten ist doppeltlogarithmisch der Amplitudenfrequenzgang |𝐹(𝑤)| auf 10⁡𝑉𝑝𝑝 normiert
gezeichnet, gegen die Frequenz, die wir vom Sinus-Signalgenerator her eingestellt haben. Zu
sehen sind zwei Kurven, jeweils für das CR- und RC-Glied. Klar erkennbar ist die Tendenz des
RC-Gliedes, dass |𝐹| zu zunehmenden Frequenzen abfällt, wohingegen das CR-Glied genau
die entgegengesetzte Tendenz zeigt. Die beiden Kurven schneiden sich an der Eckfrequenz
𝑓𝐸 = ⁡
1
. Mit 𝑅⁡ = ⁡1𝑀𝑂ℎ𝑚, 𝐶⁡ = ⁡45⁡𝑛𝐹 ergibt sich eine theoretische Vorhersage von
(2⁡π⁡R⁡C)
𝑓𝐸 ⁡ = ⁡3.53⁡𝑘𝐻𝑧. Dies kann man auch am Plot ablesen.
Auf dem zweiten Millimeterpapier erkennt man den 𝜑(𝜔) − 𝐹𝑟𝑒𝑞𝑢𝑒𝑛𝑧𝑔𝑎𝑛𝑔. Es sind wieder
zwei Kurven für CR- und RC-Glied aufgetragen, und zwar einfach logarithmisch, da auf der yAchse das Phasenintervall zwischen 0° und 90° aufgetragen ist. An der Eckfrequenz sollten
sich die beiden Kurven bei 45° treffen, dies ist nur ungefähr der Fall. Man erkennt wie
erwartet, dass der Frequenzgang des RC-Gliedes bei hohen Frequenzen gegen 90° geht und
bei niedrigen Frequenzen quasi unverändert bei 0° ankommt, während wie erwartet das CRGlied das gegenteilige Verhalten an den Tag legt. In unserem speziellen Fall hat das RC-Glied
über den großen Bereich von 10𝑘𝐻𝑧⁡𝑏𝑖𝑠⁡100𝑘𝐻𝑧 fast keinen Phasenunterschied gezeigt,
dies wurde mit den Praktikumsbetreuern diskutiert, möglicherweise kann man dies als einen
sehr guten Arbeitsbereich des Gliedes interpretieren, siehe weiter unten.
zu 2. RC-Glied als Integrierer, CR-Glied als Differenzierer
Frequenz f
100 Hz
1 kHz
6 kHz
10 kHz
100 kHz
Eingang 𝑼𝑬
10 𝑉𝑝𝑝
10 𝑉𝑝𝑝
10 𝑉𝑝𝑝
10 𝑉𝑝𝑝
10 𝑉𝑝𝑝
Amplitude 𝑼𝑨
380 mV
2,8 V
4,4 V
8,4 V
10 V
Phase
72°
57°
25°
86°
0°
In dieser Teilaufgabe geht es um das Verhalten der CR- und RC-Glieder in Abhängigkeit der
𝑓
Form des Eingangsignals. Wir haben mit sehr kleinen Frequenzen 𝑓 = ⁡0,1, ungefähr der
𝐸
𝑓
𝑓
Eckfrequenz 𝑓⁡ = ⁡3,5𝑘𝐻𝑧, also 𝑓 = ⁡1, sowie sehr hohen Frequenzen 𝑓 = ⁡10, etwa 𝑓⁡ =
𝐸
𝐸
⁡100𝑘𝐻𝑧 gearbeitet.
Man erkennt beim CR-Glied, dass es als Differenzierer tätig ist. Bei sehr hohen Frequenzen
gleicht sich das CR-Ausgangssignal an das Eingangssignal an, der Hochpass lässt das Signal
also unverändert durch, in guter Übereinstimmung mit der wegfallenden Dämpfung |𝐹| = ⁡1
und dem verschwindenden Phasenversatz⁡𝜑⁡ = ⁡0°. Bei sehr niedrigen Frequenzen wirkt das
CR-Glied als idealer Differenzierer, wie man am Besten beim Dreieckssignal erkennt, wo die
Ableitung der einfachen Steigung (±𝑎𝑡)⁡einfach die Konstante
𝑑(±𝑎𝑡)
𝑑𝑡
= (±𝑎) ist, aus dem
Rechteck wird so ein Dreieck. Der Sinus ist relativ unanschaulich, da es hier nur zum
Phasenversatz kommt, das Rechtecksignal als Eingang ist aber noch interessant, da es hier
bei den plötzlichen Flanken zu sehr großen Diracimpulsen kommt, die jeweils in die Richtung
der Veränderung zeigen, eben wie man es auch in der Theorie erwarten würde
𝑑𝜃(𝑡)
𝑑𝑡
= ∆(𝑡),
wobei Theta die Heavysidsche Thetafunktion ist und ∆⁡der Dirac-Impuls oder Dirac-Stoß.
Das RC-Glied wird hingegen zum Integrierer, und zwar bei sehr hohen Frequenzen. Bei sehr
niedrigen Frequenzen lässt es das Signal unverändert durch. Auch hier ist das Dreieckssignal
am Interessantesten, da ∫ ±𝑎𝑡 ∗ 𝑑𝑡⁡~𝑡², wir haben es also mit einer Aneinanderreihung
echter Parabeln zu tun. Dass es sich beim Ausgangssignal nicht etwa um sinusartige
Schwingungen handelt, erkennt man, wenn man die Spannungsauflösung (y-Achse) des
Oszilloskops sehr hoch einstellt: Die Steigung am Wendepunkt (höchsten- bzw niedrigsten
Punkt) des Dreieckssignals wird beim Ausgangssignal unendlich, während ein Sinus an der
Stelle flach wäre. Im Falle des RC-Glieds soll an dieser Stelle auch das Verhalten an der
Eckfrequenz diskutiert werden: Man sieht den uneleganten Übergang vom Integrierer zur
Originalfunktion: Aus den Parabeln werden hässliche gurkenförmige Kurven, aus der
Stufenfunktion werden Kurven, die an den Auf- und Entladevorgang eines Kondensators
erinnern. Das macht Sinn, den eben ein solcher ist ja in unserer Schaltung verbaut, und weit
unterhalb der Arbeitsfrequenz des Schwingkreises verhält er sich eben in erster Ordnung wie
ein Kondensator im Gleichstromkreis.