RC-Glied als Integrator

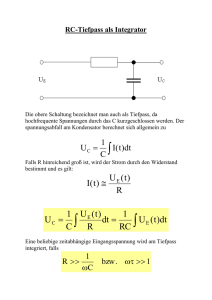
RC-Glied als Integrator
Die obere Schaltung bezeichnet man auch als Tiefpass, da hochfrequente Spannungen durch das C kurzgeschlossen werden. Der spannungsabfall am Kondensator berechnet sich allgemein zu
1
U C = ∫ I( t )dt
C
Falls R hinreichend groß ist, wird der Strom durch den Widerstand bestimmt und es gilt:
U E (t)
I( t ) ≅
R
1 U E (t)
1
UC = ∫
dt =
U E ( t )dt
∫
C
R
RC
Eine beliebige zeitabhängige Eingangsspannung wird am Tiefpass integriert, falls
1
R >>
ωC
bzw . ωτ >> 1
RC-Hochpass als Differenzierglied
Der Spannungsabfall am Ohm’schen Widerstand ergibt sich zu
U R = RI
Wird R hinreichend klein im Vergleich zum kapazitiven Widerstand
gewählt, so wird der Strom durch den Betrag von C bestimmt
dU C
I≅C
dt
In diesem Fall erhält man wegen UC ≈UE:
dU E ( t )
U R = RC
dt
Eine beliebige zeitabhängige Eingangsspannung wird am Hochpass
differenziert, falls die Bedingung
R <<
1
ωC
bzw. ωτ << 1
Sinusförmige Wechselspannungen am RC-Glied
Für
U E = U 0 sin ωt
erhält man allgemein am Ausgang des Tiefpass:
UC = −
U0
1 + (ωRC )
2
sin (ωt + ϕ ) = −
U0
1 + (ωτ )
2
sin (ωt + ϕ)
Ist die Bedingung ωτ >> 1 erfüllt, so ist die Phasenverschiebung zwischen Gesamtspannung UE und UR = 0 und zwischen UE und UC
gleich 90°. Man erhält dann:
U0
UC = −
cos(ωt )
ωRC
Dieses Ergebnis erhält man auch durch Anwendung der oben angegebenen Integrationsbeziehung.
Im Falle eines Hochpasses erhält man durch Differenzieren (im Falle
der Gültigkeit von ωτ <<1 !!!) das Resultat
U R = U 0 ωRC cos(ωt ) = U 0 ωτ cos(ωt )
Allgemein gilt :
UR = U0
ωRC
1 + (ωRC )
2
sin (ωt + ϕ)
ϕ = arctan(ωRC )
Integration einer Rechteckspannung
Gegeben sei eine periodische Rechteckspannung:
UE = +U0
für 0 < ωt < π
U E = −U0
für
π < ωt < 2 π
Die Integration dieser Spannung liefert eine linear ansteigende Spannung bis ωt = π und eine linear abnehmende Spannung im nachfolgenden Intervall bis ωt = 2π (Sägezahnspannung).
Eine Fourierzerlegung der Rechteckspannung in ein Spektrum von Sinusspannungen sollte es ermöglichen, unter Anwendung der vorherigen Ergebnisse für harmonische Spannungen zu demselben Resultat
zu gelangen. Die oben angegebene Eingangsspannung kann folgendermaßen in eine Reihe entwickelt werden:
UE = U0
4
1
1
1

(
)
(
)
(
)
ω
+
ω
+
ω
+
sin
t
sin
3
t
sin
5
t
sin (7ωt ) + .....

π
3
5
7

Das Ausgangsspannungsspektrum erhält man dann zu
∞
U C = ∑ U Cn
n =1
4U 0 ∞ cos(nω1 τ)
=−
∑ n2
πω1 τ n =1
für ungerade n = 1, 3, 5, ....
In den folgenden beiden Abbildungen ist das Amplitudenspektrum der
Eingangs- und Ausgangsspannung für n = 1 bis 11 sowie die berechnete zeitabhängige Ausgangsspannung (in der Summation bis n=9 berücksichtigt) dargestellt.
Amplitudenspektrum der Rechteckeingangs- und
Sägezahnausgangsspannung
U0 = 10V
1
14
12
Un/V
8
0,01
6
4
UCn/V
0,1
10
0,001
2
0,0001
0
1
2
3
4
5
6
7
8
9
10
11
n - Vielfaches der Grundfrequenz
Amplitudenspektrum der Eingangsspannung
Ausgangsamplitudenspektrum
0,06
15
0,04
10
0,02
5
0
0
0,02
0
0,005
0,01
0,015
-0,02
-5
-0,04
-10
-0,06
-15
t/s
berechnet für n=1 bis 9
Eingangsrechteckspannung
UE/V
UC/V
Tiefpassintegration einer Rechteckspannung
Umax = 10V ; τ = 1s ; fo = 50Hz