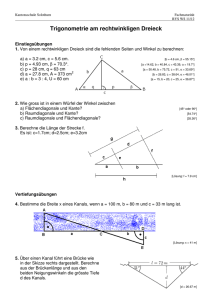
2. Klassenarbeit - mathe-physik

Gymnasium
2. Klassenarbeit
Klasse 7
1.
2.
Forme in die Prozentschreibweise um: a)
3
4
b)
0,085
Schreibe als gekürzten Bruch:
36 %
d)
9,5 %
Berechne:
a)
4 % von 120 kg
b)
14 % von 1,4 cm
c)
c)
0,15 % von 150.- EUR
3.
Eine Zehnerkarte für den Stadtbus kostet 7 EUR, ein Einzelfahrschein kostet
0,80 EUR.
Um wie viel Prozent ist die Zehnerkarte billiger als 10 Einzelfahrscheine ?
4.
Nach einer Gehaltserhöhung von 6 % erhält Herr Freudich 4240,- EUR.
Wie hoch wäre sein neues Gehalt bei einer Erhöhung um 10 % gewesen ?
5.
Eine Dose Milch enthält 200g Milch mit einem Fettgehalt von 10 %.
Wie viel Gramm Wasser muss man dazuschütten, um Milch mit einem Fettgehalt
von 4 % zu bekommen ?
GM_A0051 **** Lösungen 2 Seiten
www.mathe-physik-aufgaben.de
Gymnasium
2. Klassenarbeit
Klasse 7
Hinweis: Bearbeite die Aufgabe 2 auf dem Aufgabenzettel !
1.
2.
Forme in die Prozentschreibweise um: a)
1
5
b)
0,025
Schreibe als gekürzten Bruch:
12 %
d)
7,5 %
c)
a) Bei einer Verkehrszählung wurden
55 % PKW und 10 % LKW gezählt.
Der Rest waren Fahrräder.
Stelle dies im nebenstehenden
Kreisdiagramm dar !
b) Welchem Prozentsatz entspricht ein
Mittelpunktswinkel von 108° ?
3.
Berechne mit Dreisatz !
Nach einer Gehaltserhöhung von 6 % erhält Herr Krösus 4352 EUR.
Wie hoch war sein Gehalt vor der Erhöhung ?
4.
Ein Radio kostet 210 EUR. Dieser Preis wird zunächst um 5 % erhöht, der erhöhte
Preis später wieder um 20 % vermindert.
a) Wie teuer ist das Radio nach der Preissenkung ?
b) Um wie viel % ist der Preis insgesamt gefallen ?
GM_A0052 **** Lösungen 2 Seiten
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7
1.
2.
Berechne mit geeigneten Zwischenschritten:
a)
2 - | - 3 - | 5 - 1 3 || =
b)
(- 4 ,2) - (- 2 ,35) – (- 1 ,6) + (- 0 ,75) =
c)
-4
d)
1,8a – 2,6b – 1,6b – 2,2a – 1,3a + 3,6b =
3
5
3
1
x + (- 2 y) – (+2 x) – (- 3 y) =
4
9
8
3
Übertrage die Figur als Skizze auf das Arbeitsblatt.
a)
Warum sind in der Figur die Geraden BC und ED parallel ?
b)
Kennzeichne grün die auftretenden Wechselwinkel und braun die auftretenden
Nachbarwinkel !
c)
Berechne für β = 55°21’16’’ die Winkel α und ε.
d)
Wie muss β gewählt werden, wenn [CE den Winkel ) ACB halbieren soll ?
e)
Wie groß ist β, wenn [EC den Winkel ) BED halbieren soll ?
2c) am 09.01.04 korrigiert
GM_A0063 **** Lösungen 2 Seiten
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7
1.
Löse zuerst die inneren Klammern auf und berechne dann:
⎡ −3 7 − ( −13,7 + 24,9)⎤ ⋅ ⎡( 2 )3 − ( −3 )2 ⎤ =
⎦
⎣⎢ 10
⎦⎥ ⎣
2.
Berechne:
a)
b)
3.
( − 21 ) ⋅ 56 ⋅ ( − 41 ) ⋅ 35 =
(2 32 − 4 61 ) : ( 32 − 1039 ) =
Berechne auf zwei Arten:
(
)
( −15) ⋅ − 2 − 4 =
3 5
4.
Berechne den fehlenden Innenwinkel des Dreiecks ABC, wenn gilt:
γ = 16° 23 "
β = 59° 37'
5.
Berechne β, γ1, γ 2 .
6.
Es gelte g1 & g2 und g3 & g4 , δ = 110°, γ = 115° und ε = 60° .
Berechne )ADC , )EAD , )CBE und )ECB .
Gib jeweils eine ausreichende Begründung an !
GM_A0220 **** Lösungen 2 Seiten
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7
1.
2.
Bestimme die Lösungsmenge ! G = _
a)
x+4 =7
b)
67,3 − x = 5,75
c)
2x − 3 = 9
Berechne bzw. vereinfache !
a) ( +1,5) − ( −2,3) − 4,6
b) ( −2x) + ( −5y) − ( +6x) − ( −4y)
3.
4.
Welche Zahlen / Vorzeichen fehlen ?
a) ( −4,3) − (
) = − 6,1
b) ( −3,2) + (
5,6) = ( −
)
Welche Zahl muss man von -12,8 subtrahieren, um + 5,4 zu erhalten ?
Zeichnungen zu den Aufgaben 5 bis 6 siehe Blatt 2
5.
Konstruiere zu S den Spiegelpunkt S´ bezüglich a !
Zeichne ohne einen weiteren Punkt zu spiegeln den zu α symmetrischen Winkel α´
bezüglich a ! Welche Eigenschaft symmetrischer Geraden benützt Du dabei ?
6.
Konstruiere zu A und C und zu B und D die Symmetrieachsen !
Ist [AB] zu [CD] symmetrisch ? Begründung !
7.
Sei der Winkel α beliebig gegeben. Drücke die Winkel β1, β2 und δ durch α aus !
GM_A0281 **** Lösungen 2 Seiten (GM_L0281)
1 (2)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7
Zeichnung zu Aufgabe 5:
Zeichnung zu Aufgabe 6:
Zeichnung zu Aufgabe 7:
GM_A0281 **** Lösungen 2 Seiten (GM_L0281)
2 (2)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7
1.
a) Welche Zahl ist um 6,5 größer als - 5 ?
b) Welche Zahl liegt auf der Zahlengeraden in der Mitte zwischen - 4,8 und 3,1 ?
(Berechnung und Zeichnung !)
(
)
c) Berechne: (0,83 − 1,4) − 2 − 3,4 =
5
d) Ordne die folgenden Zahlen der Größe nach und gib das Ergebnis in Form einer
steigenden Ungleichungskette an !
−1600; 600; − 4,2; − 3 ; − 4 ; − 2 ; 4,2
5
5
3
2.
Welche der drei Terme sind zueinander äquivalent bezüglich G = { 1; 2; 3; 4 } ?
(Begründung !)
2
T1 ( x ) = ( 3x + 2 ) − 12x ;
3.
T2 ( x ) = 9x 2 + 4 ;
T3 ( x ) = 27x − 14
a) Berechne den kleineren der beiden Winkel, den die Zeiger einer Uhr um 8.07 Uhr
miteinander bilden ? (Mit Zeichnung !)
b) Welchen Drehwinkel überstreichen der kleine und der große Zeiger von obiger
Uhrzeit bis 12.00 Uhr ?
4.
a) Bringe die Winkelgrößen 19° 57'36" und 14° 55'12" auf dezimale Schreibweise !
b) Rechne 654,321° in Grad, Minuten und Sekunden um !
(Runde dabei auf ganze Sekunden !)
5.
a) Zeichne mit dem Geodreieck die Winkel der Größen ϕ = 143° und δ = 37° und
konstruiere dann daraus einen Winkel der Größe α = ϕ − 3 δ !
b) β = 46°13' 48" .
Berechne die Größe β * eines zugehörigen Komplementwinkels !
GM_A0289 **** Lösungen 3 Seiten (GM_L0289)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
1.
Gib jeweils den passenden Term an und beschreibe welche Termart vorliegt.
a) Addiere zum Quadrat von a ein Drittel von b.
b) Subtrahiere das Neunfache von x vom Dreifachen der Zahl a
b
c) Multipliziere die ganze Zahl z mit dem Produkt ihres Vorgängers und ihres
Nachfolgers.
2.
Sind Term 1 und Term 2 äquivalent ? Forme entsprechend um.
Welche Rechengesetze kommen jeweils zur Anwendung ?
T1  x  a  b   y  a  b 
3.
T2  a  x  y   b  x  y 
Berechne:
a)
b)
   8,3  20  0,44  17,7 


 p   3,5q  3 p    5p  3q  2 3 q  0,125q    5 q  p   
2
4  
8




     4
9
 
4.
Von einer Geradendoppelkreuzung ist bekannt, dass ein Winkel dreimal so groß wie
sein zugehöriger Stufenwinkel ist, welcher 37,4° beträgt.
Erstelle eine Überlegungsfigur und ermittle alle restlichen Winkel der Doppelkreuzung !
Begründungen angeben !
5.
Berechne in der Figur die Winkel  ,  und  ! Begründungen angeben !
Blatt 2 beachten !
GM_A0555 **** Lösungen 3 Seiten (GM_L0555)
1 (2)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
6.
Die Fa. Coolbox verkauft Kühlschränke. Der Chef möchte über die Umsatzentwicklung
der Jahre 2004 bis 2007 informiert werden. Sein Verkaufsleiter stellt die Umsätze
folgendermaßen dar:
a) Das Diagramm vermittelt einen falschen Eindruck. Welcher verkehrte Eindruck
ist hier wiedergegeben worden und wodurch ist er entstanden ?
b) Erstelle ein verbessertes Diagramm, das die Umsatzentwicklung realitätsnah
wiedergibt.
c) Berechne die prozentuale Zunahme zwischen 2004 und 2007.
GM_A0555 **** Lösungen 3 Seiten (GM_L0555)
2 (2)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
1.
2.
3.
Fasse so weit wie möglich zusammen:
a)
− 2 x2 + 9 3 + 7 − 1 1 x + 4 5 x2 + 2 1 x
3
5 15
7
6
14
b)
− f 2g + 2e2 f
c)
( −21x
(
4
)
2
+ e4 ⋅ 3f 2 − ( − f ) ⋅ 4g
2
(
+ ( − x ) : x 3 + x 2 ⋅ −5x 2
7
) ) : ( 3x )
2
Gib einen Term an, mit dem man für jede Breite b eines Rechtecks die zugehörige
Länge l ermitteln kann, wenn das Rechteck den Umfang 45 cm hat.
Zeichne den Graphen der Zuordnung T ( x ) = − 1 x 2 + 4,5 für − 3 ≤ x ≤ 3 !
2
4.
In einer Klasse spielen einige Schüler Geige. Doppelt so viele Schüler spielen Flöte,
und es gibt 9 Pianisten mehr als Flötisten.
Stelle einen Term für die Größe der Klasse auf, wenn jeder Schüler genau eines der
genannten Instrumente spielt !
Berechne anschließend die Größe der Klasse, wenn es 4 Streicher gibt und fünf
Schüler kein Instrument spielen.
5.
Berechne die Winkel α , β , γ und δ eines Parallelogramms ABCD, wenn β = 132°
beträgt !
6.
Wie viele Ecken hat ein Vieleck, dessen Winkelsumme 3960° beträgt ?
GM_A0556 **** Lösungen 2 Seiten (GM_L0556)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
1.
Berechne.
a)
2.
5.
−9 ⋅ ( −8 )
3 + ( 3 − 5 ) : 14
7
)
−8,4 − ( −6,93 )
c)
5 + −1 3
6
12
b)
−3 3 : 3
4 8
c)
−3,5 : − 7
10
( )
Berechne.
a)
4.
(
b)
Berechne.
a)
3.
−8 + ( −6 )
b)
−2 ⋅ 9 − ( −13 + 5 )
Schreibe zunächst ausführlich, berechne dann.
3
4
c) ( −1)
b) ( −0,5 )
a) 52
( )
c)
−2 ⋅ − 5 ⋅ ( −2,1)
6
d)
06
a) Was besagt das Assoziativgesetz der Addition ? Gib dazu ein Zahlenbeispiel
an und erläutere das Gesetz kurz mit deinen Worten.
b) Gilt das Assoziativgesetz auch für die Subtraktion ? Begründe rechnerisch.
6.
Rechne geschickt. Gib an, welches Rechengesetz du dabei anwendest.
a)
7.
− 1 − 23 + 3,1 − 2 − 0,1 + 3 − 1
6
6
2
(
34 ⋅ − 5 + 100
17
)
Finde jeweils eine Zahl, die man für x einsetzen kann, so dass die Rechnung stimmt.
a) 8 + x = −13
8.
b)
b)
x ⋅ ( − 4 ) = 120
c)
x ⋅ 0 = −14
Rotkäppchen ist auf dem Weg zu ihrer Großmutter. Sie trägt einen Korb mit etwas Brot
und Wein, welcher insgesamt 2,7 kg wiegt. Ihre Schulsachen trägt sie in einem 2 4 kg
5
schweren Rucksack auf dem Rücken. Plötzlich springen zwei kleine je 2,541 kg
wiegende Zwillingsfüchse auf sie zu. Der eine macht es sich im Korb bequem, der
andere springt mit einem Satz in den Rucksack.
Was ist nun schwerer – Korb oder Rucksack ? Notiere Deine Überlegungen.
GM_A0557 **** Lösungen 2 Seiten (GM_L0557)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
1.
Quadrate
Aus Streichhölzern – hier durch Strecken dargestellt – werden Quadrate gelegt.
a) Wie viele Streichhölzer sind jeweils für 4, 5, 6 und 10 Quadrate notwendig ?
b) Wie viele Streichhölzer sind für n Quadrate notwendig ? – Gib den Term
(vereinfacht !) an und schreibe dazu, ob dieser eine Summe, eine Differenz,
ein Produkt oder ein Quotient ist.
2.
Rechne geschickt
Zuerst den Inhalt der Klammer berechnen oder zuerst ausmultiplizieren ? Wähle den
für die Berechnung des Terms einfacheren Weg und schreibe die Schritte auf.
a)
3.
( 41 + 81 ) ⋅ 37 =
b)
(
)
13 7 − 5 =
8 52 26
Vereinfache in Schritten soweit wie möglich.
a) 1,5 ( −5 + x + 3 ) − 3 ⋅ 12 =
4.
b)
9z − x − x − 63z =
3
c)
x ⋅ ( − 4x ) − 3x ⋅ ( − x ) + 5x − x =
d)
−18 ( b + 1) − ⎡⎣3b − ( 2b − 2 ) ⎤⎦ =
Quadervolumen
a) Gib zunächst die Formeln für das Volumen V und die Oberfläche O eines
Quaders mit der Länge l, der Breite b und der Höhe h an.
b) Entwickle dann hieraus Formeln für V und O für folgenden Fall:
Die Länge l ist das Vierfache der Höhe h, die Breite b ist das Dreifache der
Höhe h.
Vereinfache die gefundenen Terme !
GM_A0558 **** Lösungen 2 Seiten (GM_L0558)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
1.
2.
Löse die Klammern auf und fasse soweit wie möglich zusammen !
(
)
a)
1 b2 7ab − 1 a2 − 3 b ⎛ ab ⎡b − 5 a ⎤ + 1 ab2 ⎞ − 1 ab2 20a + 37b
(
)
⎟ 40
4
2
4 ⎜⎝ ⎢⎣
6 ⎥⎦ 10
⎠
b)
( 6x
4
)(
) (
)(
− 9x 2 y + 11y 2 8x 2 − 7y − 13y 2 + 21x 2 y − 17x 4 11x 2 + 13y
)
In einen quaderförmigen Metallklotz
wurde ein durchgehendes Loch mit
rechteckigem Querschnitt gebohrt.
a) Gib einen allgemeinen Gleichungsansatz für das Volumen des
Restkörpers an.
b) Wie groß ist das Volumen, wenn
die Lochhöhe x = 2 m beträgt ?
3.
Gib an, um welchen Spezialfall es sich jeweils handelt:
a) Ein achsensymmetrisches Trapez mit vier gleich großen Winkeln.
b) Ein achsensymmetrisches Trapez mit vier gleich langen Seiten.
c) Eine Raute mit vier gleich großen Winkeln.
d) Ein Drachen mit vier gleich langen Seiten.
4.
In nebenstehender Figur
sind die Geraden g und h parallel.
Außerdem gelte:
α = 120° und α − β = 40° .
Berechne die Winkel β , δ , ω , µ , ε , τ !
Begründe sämtliche Rechenschritte stichpunktartig.
5.
Zeichne jeweils ein punktsymmetrisches Sechseck, das
a) keine Symmetrieachsen hat.
b) genau zwei Symmetrieachsen und gleich lange Seiten hat.
GM_A0559 **** Lösungen 2 Seiten (GM_L0559)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
1.
Berechne jeweils zuerst alle Termwerte zu den angegebenen Einsetzungen und
ergänze dann passend „äquivalent“ oder „nicht äquivalent“.
e
0
1
6
f
5
6
1
T1 ( e; f ) = e f (1 + e )
T2 ( e; f ) = 2e2 f
2.
3.
Vereinfache soweit wie möglich:
a)
−3,5ab − ( 6ac + 1,3b c ) − ( 0,7bc − ab ) =
b)
( −3u)
c)
6x ⋅ 3xy + 0,6xy ⋅ ( − 4y ) + 2,4x 2 y − x ⋅ ( −2y ) ⋅ ( −3x ) =
d)
(z
3
3
(
)
⋅ − 1 u v ⋅ ( 2v ) =
2
4
)(
)
− 3 z 6 + 11z 6 − z3 2 z 2 − 4 z 2 =
7
Martina legt aus Stecknadeln Figuren, die aus Sechsecken aufgebaut sind:
a) Wie viele Stecknadeln benötigt sie, wenn sie eine Figur mit drei bzw. vier
Sechsecken in einer Reihe legen will ?
b) Wie könnte ein Term lauten, der angibt, wie viele Stecknadeln für eine Figur
mit n Sechsecken benötigt werden ?
Tipp: Überprüfe den gefundenen Term mit Hilfe der obigen Zeichnung !
c) Wie viele Stecknadeln benötigt sie für eine Figur mit 200 Sechsecken ?
4.
a) Erstelle einen Term T(a), bei dem a = 2 als Einsetzung verboten ist !
b) Schreibe als Produkt: a2 − a + a3
c) Kreuze an, aus wie vielen Summanden die Summe besteht, die man nach dem
Ausmultiplizieren des Terms a2 + a + 1 b2 − b5 + b11 − 1 c 3 − 1 erhält:
(
12
9
)(
8
)(
24
)
10
Blatt 2 beachten !
GM_A0560 **** Lösungen 2 Seiten (GM_L0560)
1 (2)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
d) Das abgebildete Dreieck hat den Flächeninhalt 1 a2 + a .
2
Was lässt sich daraus über die Länge der Seite b
aussagen ?
(Hinweis: Schreibe die Summe als geeignetes Produkt !)
5.
2
Bei ihren Hausaufgaben hat Eva zum gegebenen Term T ( x ) = x − 4 für
2
einige x ∈ ] die Termwerte und die zugehörigen Einsetzungen im Koordinatensystem
veranschaulicht.
Falls Du der Meinung bist,
Eva hat alle Punkte richtig
eingezeichnet, dann füge
einen weiteren passenden
Punkt in diesem Koordinatensystem hinzu.
Falls Du aber der Meinung
bist, ein Punkt oder mehrere
Punkte sind falsch eingezeichnet worden, dann
markiere diese(n) farbig
(nicht rot !) und zeichne
korrekt ein.
6.
Grundwissen
Berechne den Oberflächeninhalt eines Quaders, der 2 cm hoch, 4 cm breit und
dreimal so lang wie breit ist !
GM_A0560 **** Lösungen 2 Seiten (GM_L0560)
2 (2)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
1.
2.
Vereinfache folgende Terme so weit wie möglich !
(
)
(
)
a)
⎧
⎫
− −a − a2 + ab − ⎨ − 5 a2 + 6,9ab − 2 4 − ⎡⎢ −1,2a2 + 3 1 a − 2 − 1 a − ab ⎤⎥ − 6,9a2 ⎬
5 ⎣
5
5
⎦
⎩ 2
⎭
b)
32 x13 y 3 ⋅ 64 ⋅ y 7
x 7 ⋅ 512 x 3 ⋅ y 2 ⋅ x y 6 ⋅ 8x 4 y
(
)
a) Wann heißen zwei Terme äquivalent ?
b) Welche Möglichkeiten gibt es, um die Äquivalenz zweier Terme nachzuweisen ?
3.
Auf einem Parkplatz befinden sich n Motorräder, zehnmal so viele PKW und außerdem
k Fahrräder. Beschreibe durch Terme:
a) die Gesamtzahl der Kraftfahrzeuge auf dem Parkplatz
b) die Gesamtzahl der Reifen auf dem Parkplatz
c) die größtmögliche Anzahl an Personen, die mit diesen Fahrzeugen befördert
werden kann, wenn in jedem PKW höchstens fünf, auf jedem Motorrad
höchstens zwei und auf einem Fahrrad höchstens eine Person Platz haben.
4.
5.
Bei einem Festessen nehmen n Familien mit je 4 Personen teil. Jedes Gedeck
besteht aus zwei Tellern, einem Messer, einer Gabel, zwei Löffeln, einem Weinglas
und einem Wasserglas. Für jeweils 4 Personen wird eine Suppenschüssel und für
jeweils 2 Personen eine Platte mit Beilagen und eine Platte Fleisch aufgetragen.
Was beschreiben die folgenden Terme ?
a)
T ( n ) = 4n
b)
T ( n ) = 2 ⋅ 4n + 4 ⋅ 4n + 2 ⋅ 4n
Gegeben ist der Term T ( a ) = 2a − 2 . Grundmenge G = _ .
Erstelle eine Wertetabelle für ganzzahlige Werte a im Bereich [ − 2; + 3 ] und
veranschauliche den Term durch ein Liniendiagramm !
GM_A0561 **** Lösungen 2 Seiten (GM_L0561)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
1.
3 x 2 − 2x + 1
.
Gegeben ist der Term T ( x ) = 2 2
x −4
a) Welche Werte darf man nicht für die Variable x einsetzen ? Warum ?
b) Berechne die Termwerte für x = − 4 und x = 2
3
2.
Angelika will sich für ihr neues Vertragshandy zwischen zwei Tarifen A und B mit
monatlicher Grundgebühr entscheiden:
A: Grundgebühr 5 €, 0,15 € pro Minute
B: Grundgebühr 10 €, 30 Gesprächsminuten frei, dann 10 ct. pro Minute.
a) Die Variable x sei die Anzahl der von Angelika in Anspruch genommenen
Gesprächsminuten. Gib einen Term A(x) an, mit dem sie die monatlichen
Handykosten in € in Abhängigkeit von der Variablen x berechnen kann.
Wie lautet der zu A(x) entsprechende Term B(x) für x > 30 ?
b) Ergänze die Tabelle und stelle damit beide Tarife graphisch in einem
Koordinatensystem dar. Lies daraus ab, ab welcher Gesprächsdauer Tarif B
günstiger ist als Tarif A.
(Zum Zeichnen: x - Achse: 1 cm = 10 min, y - Achse: 1 cm = 2 €)
x
10
25
50
75
100
A (x)
B (x)
c) Bei welcher monatlichen Gesprächsdauer x ist Tarif B sogar um 15 € günstiger
als Tarif A ?
3.
Schorsch Schlampig hat mit einem Term T(a) die folgende Wertetabelle erstellt:
a
2
4
6
10
T(a)
6
9
12
18
-1
24
Leider machte er seinem Namen alle Ehre und vergaß den dabei verwendeten Term.
Bestimme T(a) und ergänze die beiden fehlenden Werte in der Tabelle.
4.
11
T2 ( y ) = 1,5 ⋅ ( 6y − 9 − 3y ) + 14 y
T1 ( y ) = 3,5 ⋅ ( 2y − 1) − 6 ⋅ 3,5 ⋅ 25%;
3
7
Vereinfache beide Terme soweit wie möglich !
Wie muss man den zweiten Term verändern, damit er äquivalent zum ersten
Term ist ?
GM_A0562 **** Lösungen 3 Seiten (GM_L0562)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
1.
a) Was bedeutet „Äquivalenz“ von Termen ? Gib die genaue Definition an und
erläutere wie man vorgehen muss, um Äquivalenz zu zeigen oder zu
widerlegen. Begründe Deine Aussagen !
b) Betrachte folgende Terme zur Grundmenge _ :
S ( x ) = 3x ⋅ ( x − 1)
T ( x ) = 3x 2 − 3x
U( x ) =
x2 + 1
3x ⋅ ( x − 1)
Bestimme die größtmöglichen Definitionsmengen zu den drei Termen !
DS =
DT =
DU =
c) Welche der Terme S, T und U aus Teilaufgabe b) sind äquivalent, welche
nicht ? Begründe Deine Antwort exakt !
2.
Berechne nachstehenden Ausdruck. Das Ergebnis soll als gekürzter reiner Bruch
angegeben werden.
(5 72 − 6 39 ) ⋅ ( −1,25) =
3.
Betrachte folgende Muster:
M(1)
XXX
M(2)
M(3)
XX
XXXX
XXXXX
XXXXXXX
M(4)
a) Versuche, die Folge der Muster durch ein weiteres Element M(4) fortzusetzen.
Bitte zeichne dieses in obige Grafik !
b) Stelle einen allgemeinen Term A(n) auf, der die Anzahl A(n) der „Kreuzchen“ für
das n-te Muster M(n) angibt. Vereinfache den Term so weit wie möglich !
c) Kommt in dieser Folge ein Muster mit 40 Kreuzchen vor ?
Begründe Deine Antwort durch Rechnung !
4.
Für ein Rennen soll ein Ruderboot mit 8 Ruderinnen besetzt werden. Dabei muss die
Steuerfrau auf jeden Fall hinten sitzen und die leichteste Ruderin auf jeden Fall vorne.
Auf wie viele Arten kann das Ruderboot mit den 8 Sportlerinnen besetzt werden ?
GM_A0563 **** Lösungen 2 Seiten (GM_L0563)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
1.
Vereinfache folgende Terme so weit wie möglich:
a)
3,2 x − 2,7y + 1,5 x + 0,8y − 4 ⋅ 0,6 x
b)
− ( 2a − 3b ) + 1 5b − 1 a + a 3 + 2a
2
3
4
c)
0,5 ( − 4 z + 3b ) + 2 z − 1 1 b
2
(
) (
)
2.
Ein Tischtennisball wird 1,25 m über dem Boden fallen gelassen.
Nach jedem Auftreffen auf den Boden springt er wieder hoch, verliert dabei aber jedes
Mal 20% an Höhe.
Wie oft erreicht er noch eine Höhe von mehr als 0,5 m ?
3.
Frau Meier passt eine neue Vorhangstange an. Zunächst sägt sie 80% von der Stange
ab. Das größere Stück wird anschließend auf 90% seiner Länge gekürzt, so dass die
Stange schließlich nur noch 1,80 m lang ist.
Welche Länge hatte die Stange, als Frau Meier sie im Baumarkt kaufte ?
4.
Der nebenstehende Turm ist aus Zündhölzern aufgebaut.
a) Gib einen Term T(n) an, mit dessen Hilfe man die Zahl
der benötigten Zündhölzer für einen Turm mit n Stockwerken berechnen kann.
b) Wie viele Stockwerke kann man höchstens bauen,
wenn man 100 Zündhölzer zur Verfügung hat ?
Wie viele Hölzer bleiben dann übrig ?
Blatt 2 beachten !
GM_A0564 **** Lösungen 2 Seiten (GM_L0564)
1 (2)
www.mathe-physik-aufgaben.de
Gymnasium
2. Mathematikschulaufgabe
Klasse 7 / (G8)
5.
Lukas hat in einer Umfrage zum Thema „Taschengeld“ ermittelt, dass die 125
SchülerInnen der 7. Jahrgangsstufe seines Gymnasiums im Monat November
insgesamt 2.050 € Taschengeld erhalten haben.
Davon haben sie 410 € für Süßigkeiten, 238 € für Kleidung, 82 € für Zeitschriften
und Bücher, 154 € für Kino und CDs, 123 € für Geschenke, 308 € für Ersparnisse
und den Rest für „Sonstiges“ ausgegeben.
Gib an, welche der folgenden Schlüsse Du in Bezug auf die SchülerInnen dieser
7. Klassen im Monat November ziehen kannst („9“) und welche nicht („8“).
Kreuze an !
6.
9
8
Jeder Schüler und jede Schülerin erhielt im November
Taschengeld.
o
o
Im Durchschnitt erhielt jeder Schüler der 7. Jahrgangsstufe 16,40 €
Taschengeld.
o
o
Im Durchschnitt gab jede Schülerin am meisten für Kleidung aus.
o
o
Elmar, Schüler der Klasse 7c, gab für Kino und CDs mehr aus als
für Bücher und Zeitschriften.
o
o
Im Durchschnitt erhielten Schüler ebenso viel Taschengeld wie
Schülerinnen.
o
o
Im Durchschnitt gaben alle Schüler der 7. Klassen für Süßigkeiten
20% ihres Taschengeldes aus.
o
o
Gegeben ist das Dreieck ABC (siehe Zeichnung).
a) Bestimme die Winkel α , β , γ sowie den sog. Außenwinkel β ' !
b) Die Gerade g durch den Punkt A ist parallel zur Strecke [BC]. Berechne den
Winkel δ !
GM_A0564 **** Lösungen 2 Seiten (GM_L0564)
2 (2)
www.mathe-physik-aufgaben.de