Lösungsblätter - minus-p

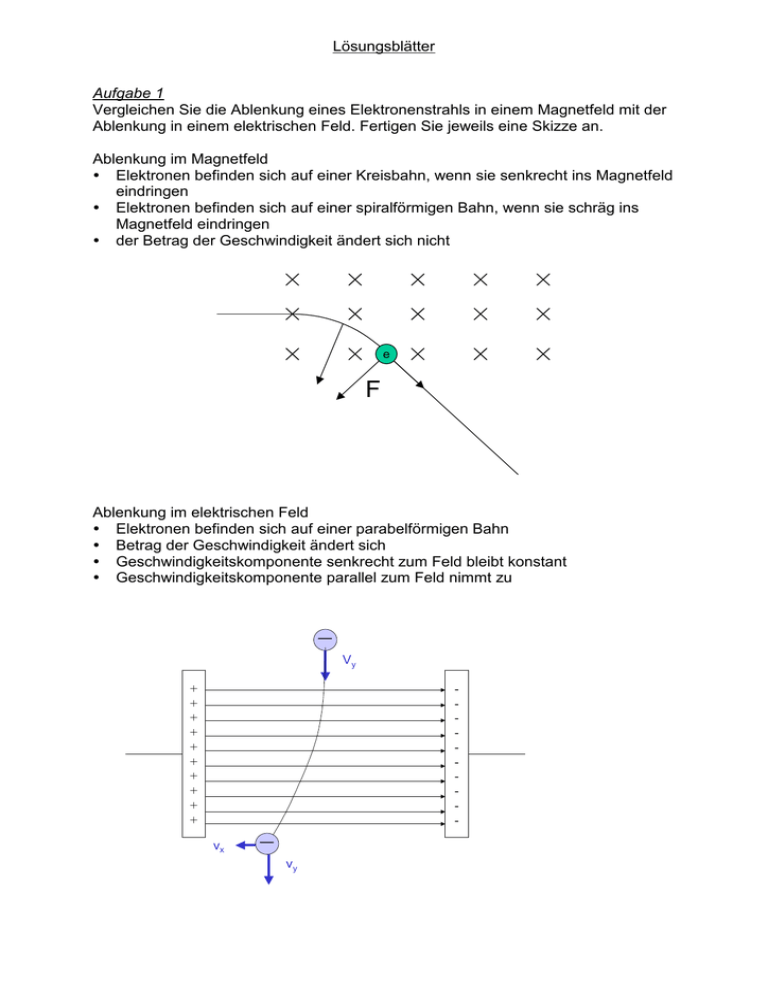
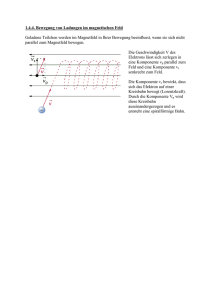
Lösungsblätter
Aufgabe 1
Vergleichen Sie die Ablenkung eines Elektronenstrahls in einem Magnetfeld mit der
Ablenkung in einem elektrischen Feld. Fertigen Sie jeweils eine Skizze an.
Ablenkung im Magnetfeld
Elektronen befinden sich auf einer Kreisbahn, wenn sie senkrecht ins Magnetfeld
eindringen
Elektronen befinden sich auf einer spiralförmigen Bahn, wenn sie schräg ins
Magnetfeld eindringen
der Betrag der Geschwindigkeit ändert sich nicht
e
F
Ablenkung im elektrischen Feld
Elektronen befinden sich auf einer parabelförmigen Bahn
Betrag der Geschwindigkeit ändert sich
Geschwindigkeitskomponente senkrecht zum Feld bleibt konstant
Geschwindigkeitskomponente parallel zum Feld nimmt zu
_
Vy
+
+
+
+
+
+
+
+
+
+
vx
-
_
vy
Lösungsblätter
Aufgabe 2
a) Erläutern Sie den Hall-Effekt.
Befindet sich ein stromdurchflossener (flächenhafter) elektrischer Leiter in einem
Magnetfeld, entsteht senkrecht zur Bewegungsrichtung der Ladungsträger einer
Spannung. Diese sogenannte Hall-Spannung hängt von folgenden Größen ab:
Größe der magnetischen Flussdichte
Größe des elektrischen Stromes
Abmessungen des Leiters
Leitfähigkeit des Materials
Aufbau:
e
-
F
v
+
V
Durch Anlegen einer Spannung an die Probe fließt ein Strom. Die Ladungsträger
bewegen mit einer mittleren Geschwindigkeit v. Durch die Lorentz-Kraft wird der
Ladungsträger senkrecht zu seiner Bewegungsrichtung abgelenkt.
Hierdurch kommt es auf der entsprechenden Seite des Leiters zu einem
Elektronenüberschuss während es auf der gegenüberliegenden Seite im selben
Maße zu einem Elektronenmangel kommt. Es entsteht also eine Spannung.
b) In einer Messreihe wird die Hall-Spannung UH in Abhängigkeit von der
Flussdichtes des Magnetfeldes gemessen.
B in mT
0,15
0,33
0,49
0,67
UH in µV
3,2
6,5
9,7
12,9
Bestimmen Sie eine Gleichung UH(B).
Idee: Beide Größen sind proportional.
Deshalb bestimmt man am besten den Proportionalitätsfaktor, indem man die
beiden Größen dividiert.
✙V
U H l 20 mT $ B
c) Bestimmen Sie die maximale-Hallspannung, wenn sich die Hall-Sonde im
Magnetfeld der Erde mit B = 5 $ 10 −5 T befindet.
✙V
U H l 20 mT $ 5 $ 10 −2 mT =1✙V
Lösungsblätter
Aufgabe 3
Ein Elektronenstrahl wird mit einer Beschleunigungspannung von 280 V erzeugt.
Dieser Strahl tritt senkrecht zu den Feldlinien eines homogenen Magnetfeldes mit
einer Flussdichte von 1,1 mT ein.
a) Berechnen Sie den Radius der Kreisbahn.
Q $ U = m $ v 2 x $2
2
2QU = mv 2 x +m
2QU
2
m =v
v=
2QU
m
2
Q $ v $ B = m $ vr x $r
r $ Q $ v $ B = m $ v 2 x +v
r$Q$B = m$v
r= m$v
Q$B
r = 0, 051m = 5, 1cm
v = 9.924.000 m
s
b) Berechnen Sie den Radius der Kreisbahn, wenn die Beschleunigungsspannung
um 10% vergrößert wird.
U = 308V
v=
2QU
m
v = 10.408.500 m
s
r= m$v
Q$B
r = 0, 0538m = 5, 38cm
Aufgabe 4
Mit einem Zyklotron lassen sich Elementarteilchen mit der Ladung Q und der Masse
m beschleunigen.
a) Beschreiben Sie den Aufbau und die Wirkungsweise eines Zyklotrons.
Aufbau:
Es besteht aus 2 halnkreisförmigen Dosen. Diese sind mit einem
Hochfrequenzgenerator verbunden. Sie befinden sich einem senkrechten
homogenen Magnetfeld.
Lösungsblätter
Funktionsweise:
Die Teilchen werden innerhalb der Dosen auf Kreisbahnen gezwungen und
zwischen den Dosen durch das elektrische Feld beschleunigt. Dadurch vergrößert
sich die Geschwindigkeit und der Radius der Kreisbahn. An einer geeigneten Stelle
werden sie durch eine Elektrode herausgelenkt und stehen für Experimente zur
Verfügung.
b) Skizzieren Sie ein v-t-Diagramm für ein Elementarteilchen, dass innerhalb von
einer Runde beschleunigt wird.
c) Weisen Sie nach, dass die Umlaufzeit unabhängig vom Bahnradius ist.
Hinweis: Man vernachlässigt den Spalt zwischen den Dosen.
Rechnung:
T = sv = 2 $ v✜ $ r
m$v
2 $ ✜ $ Q$B
T=
= 2$✜$m
v
Q$B
Nebenrechnung:
2
Q $ v $ B = m $ vr
r= m$v
Q$B
Lösungsblätter
Aufgabe 5
v
0 in ein Magnetfeld mit einer
0
Bx
→
c) B = B y eingeschossen.
0
→
Ein Proton wird mit einer Geschwindigkeit von v =
→
Flussdichte von a) B =
0
By
0
→
b) B =
Bx
0
0
Berechnen Sie jeweils die Lorentzkraft.
→ →
FL = Q $ v % B
=Q$
v
0 %
0
0
By
0
0
0
=Q$
v $ By
=
Bx
0
0
0
=Q$ 0
0
0
0
0
Bx
By
0
0
0
=Q$
v $ By
0
0
Q $ v $ By
→ →
FL = Q $ v % B
=Q$
v
0 %
0
=
→ →
FL = Q $ v % B
=Q$
v
0 %
0
=
0
0
Q $ v $ By
Aufgabe 6
Ein Elektron wird einem Kondensator mit U = 200 V und d = 3 cm beschleunigt.
a) Berechnen Sie die Beschleunigung.
F = Q$E = Q$ U
d
F = Q$U
a= m
m$d
a = 1, 17 $ 10 15 m2
s
b) Berechnen Sie die Zeit für die Beschleunigungsphase.
s = d = a $ t2
2
t=
2s
a
t = 7, 15 $ 10 −9 s